Статистическая обработка случайной величины Х - стаж работы

1. Статистическая обработка результатов эксперимента в случае выборки большого объема (n≥50) начинается с группировки выборочных значений, то есть с разбиения наблюдаемых значений СВ на к частичных интервалов равной длины и подсчета частот попадания значений СВ в частичные интервалы.

Сделаем группировку наблюдаемых значений. Оптимальную длину интервала определим по формуле Стэрджеса:

h= ,

где Хmax,Хmin – соответственно максимальное и минимальное выборочные значения СВ Х- стаж работы, n-объем выборки. Если h окажется дробным, то за величину интервала нужно взять, либо ближайшее целое число, либо ближайшую несложную дробь.

Для СВ Х- стаж работы n=100, Хmax=90, Хmin=15

h=

В качестве левого конца первого интервала возьмем величину, равную

а1= Хmin- . Если аi – начало i-ого интервала, тогда

а2= а1+ h=10+10=20

а3= а2+ h=20+10=30

а4= а3+ h=30+10=40

а5= а4+ h=40+10=50

а6= а5+ h=50+10=60

а7= а6+ h=60+10=70

а8= а7+ h=70+10=80

а9= а8+ h=80+10=90

Составим таблицу.

Вспомогательная таблица для расчета числовых характеристик выборки.

Таблица 1

Интервалы (аi; аi+1]	Середины интервалов	Подсчет частот	Частоты ni	Относительные частоты Wi=ni/n	Накопительные относительные частоты
(10;20]				0.05	0.05
(20;30]				0.10	0.15
(30;40]				0.17	0.32
(40;50]				0.20	0.52
(50;60]				0.18	0.70
(60;70]				0.15	0.85
(70;80]				0.12	0.97
(80;90]				0.03	1.00

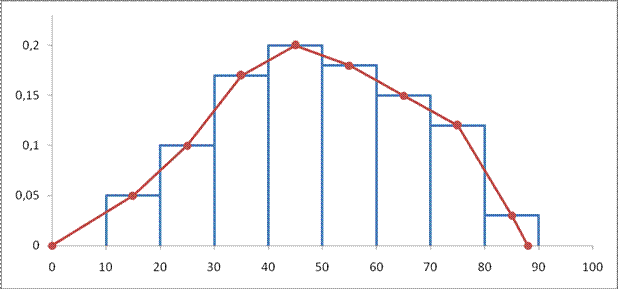
2. Первый и пятый столбцы таблицы 1 составляют интервальный статистический ряд относительных частот, графическое изображение которого – гистограмма относительных частот (ступенчатая фигура на рисунке 1).

Дискретный статистический ряд относительных частот задается вторым и пятым столбцами, графическое изображение которого – полигон относительных частот (изображен на рисунке 1 ломаной линией).

3. Эмпирическая функция распределения F^*(x) выборки служит для оценки функции распределения F(x) генеральной совокупности. Функция F^*(x) определяет для каждого значения x относительную частоту события X<x:

F^*(x) =

где nx –число выборочных значений, меньших х; n- объем выборки. Шестой столбец таблицы 1 содержит накопленные частоты, то есть значения эмпирической функции распределения F^*(x), они относятся к верхней границе частотного интервала.

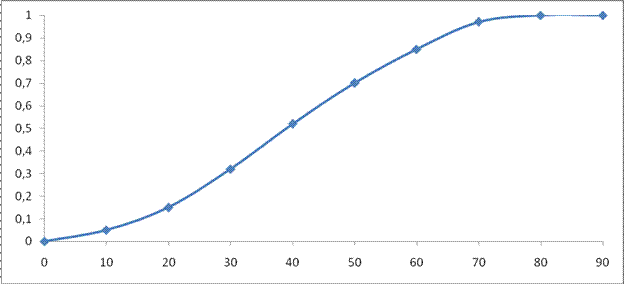
Эмпирическая функция распределения F^*(x) имеет вид:

F^*(x) =

График эмпирической функции распределения F^*(х) изображен на рисунке 2 (для непрерывных распределений значения F^*(х) распространяются на интервалы линейным интерполированием).

4. Для вычисления числовых характеристик выборки (, Дв, Sx, Ax*, Эx*) удобно использовать таблицу 2, где в первых двух столбцах приведены сгруппированные исходные данные, а остальные столбцы служат для вычисления числовых характеристик.

Выборочное среднее вычисляют по формуле:

,

где m – число интервалов, xi-середины интервалов(шт).

=(15*5+25*10+35*17+45*20+55*18+65*15+75*12+85*3)/100=4940/100=49.4

Выборочное среднее дает усредненное значение количества деталей для данной выборки.

Таблица для расчета числовых характеристик выборки.

Таблица 2

Середины интервалов xi	Частоты ni	xi-
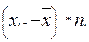
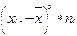
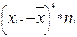
		-34.4	-172	5916.8	-203537.9	7001704.4
		-24.4	-244	5953.6	-145267.8	3544535.3
		-14.4	-244.8	3525.12	-50761.7	730968.9
		-4.4	-88	387.2	-1703.7	7496.2
		5.6	100.8	564.48	3161.1	17702.1
		15.6		3650.4	56946.2	888361.3
		25.6	307.2	7864.32	201326.6	5153960.8
		35.6	106.8	3802.08	135354.0	4818604.1
∑		----			-4483.2

Выборочную дисперсию для сгруппированных данных вычисляют по формуле:

Дв(х)= ,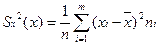

Дв(х)=31664/100=316.64

Выборочное среднее квадратическое отклонение находят по формуле:

Sx=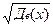

Для случайной величины Х Sx= 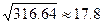(годов).

Оно показывает разброс выборочных значений хi относительно выборочного среднего =49.4.

Выборочные коэффициенты асимметрии и эксцесса вычисляют по формулам:

Ax*= ,

Эx*= ;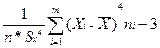

Используя суммы из последних строк шестого и седьмого столбцов таблицы 2, получим:

Ax*= -4483.2/100*(17.8)³ = -4483.2/563975.2= -0.00795

Эx*= 22163333.1/100*(17.8)⁴= 22163333.1/10038758.56= -0.7922

Ax*≠0 говорит о несимметричности полигона (гистограммы) относительно выборочного среднего . Отрицательный знак выборочного коэффициента эксцесса показывает, что полигон менее крут чем нормальная кривая.

5. Мы предварительно предполагаем, что СВ Х – стаж работы, распределена нормально по совокупности следующих признаков.

Вид полигона и гистограммы относительных частот напоминает нормальную кривую (кривую Гаусса).

Выборочные коэффициенты асимметрии Ax*= -0.00795 и Эx*= - 0.7922отличаются от значений асимметрии и эксцесса для нормального распределения (которые равны нулю) не более, чем на утроенные средние квадратические ошибки их определения.

|Ax*|=|-0.00795|<0,7161=3*SА,

|Эx*|=|-0.7922|<1,3917=3*Sэ,

где SА=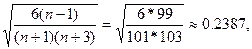

Sэ=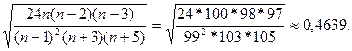

Можно предположить, что стаж работы (СВ Х) изменяется под действием большого числа факторов, примерно равнозначных по количеству.

Итак, по совокупности указанных признаков, можно предположить, что распределение СВ Х- стаж работы является нормальным.

6. Функция плотности нормального распределения имеет вид:

В качестве неизвестных параметров α и σ возьмем их точечные оценки =49.4 и Sx=17.8 соответственно. Тогда дифференциальная f(x) и интегральная F(x) предполагаемого нормального закона распределения примут вид:

; F(x)=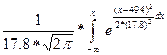

7. Гипотезу о том, что генеральная совокупность, из которой извлечена выборка, распределена по предполагаемому нормальному закону, назовем нулевой (Н0:Х N(α,σ)), тогда На:Х N (α,σ). Проверим ее с помощью критерия согласия Пирсона.

Согласно критерию Пирсона сравниваются эмпирические ni(наблюдаемые) и теоретические n*pi(вычисленные в предположении нормального распределения) частоты. В качестве критерия проверки нулевой гипотезы принимается случайная величина:

набл=

по таблице критических точек распределения по заданному уровню значимости α и числу степеней свободы v=S-r-1 (S- число интервалов, r-число параметров предполагаемого распределения СВ Х) находится критическое значение (α,v).

Если набл≤ кр, то считается, что данный критерий не дают оснований для отклонения гипотезы при данном уровне значимости α=0,05. в противном случае считается, что гипотеза не согласуется с экспериментальными данными и ее надо отвергнуть.

Если проверяется гипотеза о нормальном распределении, то вероятности рi рассчитываются с помощью функции Лапласа Ф(х):

рi=Р(xi<X≤xi+1)=Ф

где х=49.4 – выборочное среднее;

Sх=17.8 – выборочное среднее квадратическое отклонение.

p1=P(-∞<x≤20)=Ф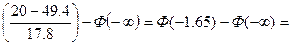

-Ф(1.65)+Ф(∞)=-0.4505+0,5=0,0495

p2=P(20<x≤30)=Ф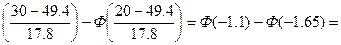

-Ф(1.1)+Ф(1.65)= -0.36433+0,4505=0,08617

p3=P(30<x≤40)=Ф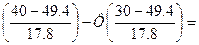

-Ф(0.53)+Ф(1.1)= -0.2019+0.36433=0.16243

p4=P(40<x≤50)=Ф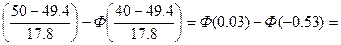

Ф(0.03)+Ф(0.5)=0,0120+0,2019=0.2139

p5=P(50<x≤60)=Ф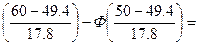

Ф(0.59)-Ф(0.03)=0.2224-0.01197=0,21043

p6=P(60<x≤70)=Ф

0,3770-0,2224=0,1546

P7=P(70<x≤80)=Ф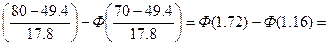

0,4573-0,3770=0,0803 P8=P(80<x<∞)=Ф

0,5-0,4573=0,0427

Вычисления сведем в таблицу 3. количество интервалов S=8.

Так как предполагается нормальное распределение имеющее два параметра (математическое ожидание α и среднее квадратическое отклонение σ), поэтому r=2, тогда число степеней свободы v=S-r-1=8-2-1=5

Таблица 3

Расчетная таблица для вычисления набл

Интервалы (xi;xi+1]	Частоты эмпирические, ni	Вероятности pi	Теоретические частоты,
-∞;20]		0,0495	4,95	1,2375E-06
(20;30]		0,08617	8,617	0,001648164
(30;40]		0,16243	16,243	0,000930803
(40;50]		0,2139	21,39	0,004132762
(50;60]		0,21043	21,043	0,0194855
(60;70]		0,1546	15,46	0,000327134
(70;80]		0,0803	8,03	0,012656003
(80;90]		0,0427	4,27	0,000688708
∑		1,0	100,00	набл=0,03987

Значение набл=0,03987

В таблице критических точек распределения по уровню значимости α=0,05 и числу степеней свободы v=5 найдем критическое значение кр(0,05;)=11,07.

Так как набл > кр, то считаем, что есть основания для отклонения нулевой гипотезы при заданном уровне значимости α=0,05.

Построим график эмпирической функции f(x). Для этого из середины частичных интервалов восстановим перпендикуляры высотой равной pi-вероятностям попадания СВ Х-стаж работы в соответствующий частичный интервал. На рисунке 3 концы перпендикуляров отмечены точками, полученные точки соединены плавной кривой.

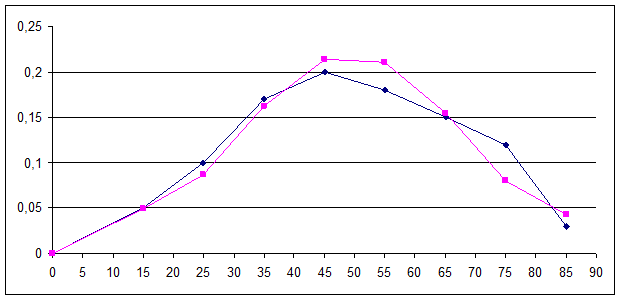
Сравнение полигона относительных частот и нормальной кривой показывает, что построенная нормальная кривая удовлетворительно сглаживает полигон.

8. Найдем интервальные оценки параметров нормального закона распределения. Для нахождения доверительного интервала, покрывающего математическое ожидание СВ Х- стаж работы, найдем по таблицам квантилей распределения Стьюдента по заданной доверительной вероятности 1-α=γ=0,95 и числу степеней свободы v=n-1=100-1=99 число tγ=1,984.

Вычислим предельную погрешность интервального оценивания:

εх= tγ* =1,984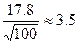

Запишем искомый доверительный интервал для математического ожидания α:

- εх<α< + εх,

49.4-3.5<α<49.4+3,5

45.9<α<52.9.

Если будет произведено достаточно большое число выборок объема n СВ Х-стаж работы, из одной и той же генеральной совокупности, то в 95% выборок доверительный интервал (45.9;52.9)покроет математическое ожидание α, и только в 5% выборок математическое ожидание может выйти за границы доверительного интервала.

Для нахождения доверительного интервала, покрывающего неизвестное среднее квадратическое отклонение σ с заданной вероятностью 1-α=γ=0,95, найдем по γ=0,95 и числу степеней свободы v=n-1=100-1=99 два числа γ1=0,878 и γ2=1,161. Искомый доверительный интервал равен:

γ1*Sx<σ< γ2*Sx,

0,878*17.8<σ<1,161*17.8,

15.6<σ<20.7

Если будет произведено достаточно большое число выборок объема n СВ Х- стаж работы, из одной и той же генеральной совокупности, то в 95 % выборок доверительный интервал (0,827;1,094) покроет среднее квадратическое отклонение σ, и только в 5% среднее квадратическое отклонение σ может выйти за границы доверительного интервала (15.6;,20.7).

ВЫВОД

Была проведена исследовательская работа над случайной двумерной величиной Х- кол-во обработанных деталей, шт.; У- время непрерывной работы станков, ч.Были построены интервальный и дискретный статистически ряды распределения частот и относительных частот, гистограммы и полигоны относительных частот, эмпирические функции распределения. Были вычислены числовые характеристики выборки: выборочную среднюю, выборочную дисперсию, выборочные коэффициенты асимметрии и эксцесса. Для Х- кол-во обработанных деталей и для У- время непрерывной работы станков, ч. несимметричный полигон (гистограмма) Правосторонняя асимметрия данного распределения, и полигон менее крут чем нормальная кривая.

Х- кол-во обработанных деталей, шт.; У- время непрерывной работы станков, ч. распределены по нормальному закону, это видно исходя из механизма их образования, по виду гистограммы и полигона относительных частот и по значениям выборочных коэффициентов асимметрии и эксцесса.

Далее были найдены точечные оценки параметров нормального закона распределения, и записаны функции плотности распределения вероятностей для Х- кол-во обработанных деталей, шт.; и для У- время непрерывной работы станков, ч.

Проверила с помощью критерия согласия Пирсона гипотезу о том, что выборка извлечена из генеральной совокупности с предполагаемым нормальным законом распределения. Была приняты гипотезы и найдены интервальные оценки параметров нормального закона распределения

И теперь проанализировав значения Х- кол-во обработанных деталей, шт.; У- время непрерывной работы станков, ч. провела корреляционный анализ: составила корреляционную таблицу; нашла выборочный коэффициент корреляции; проверила значимость выборочного коэффициента корреляции r_в ;построила корреляционное поле и по характеру расположения точек на нем подобрать общий вид функции регрессии; нашла эмпирические функции регрессии У- время непрерывной работы станков, ч.на Х- кол-во обработанных деталей, шт.;, X на Y и построила их графики.

В результате было выявлено, что математическая статистика основана на теории вероятности, изучающая методы сбора и обработки результатов наблюдений, с целью выявления закономерностей. Я рассматривала методы, позволяющие делать научно обоснованные выводы о числовых значениях параметров распределения генеральной совокупности по случайной выборке, о неизвестной функции распределения и плотности распределения, о корреляционной зависимости одной случайной величины Х от другой У по случайным выборкам, проверять статистические гипотезы на основе выборочных данных.

Заключение.

В результате проведенной работы мной установлено, что случайные величины Х-количество обработанных деталей и У- время непрерывной работы станков, распределены по нормальному закону распределения и между ними существует корреляционная зависимость.

Список используемой литературы.

1. Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. - М.:Высш. школа, 1997.-479с.

2. Сборник задач по математике для вузов. – Ч.З. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/Под ред. А.В. Ефимова. – М.:Наука, 1990.-348с.

3. Шушерина О.А. Математическая обработка экспериментальных данных: Методические указания к лабораторной работе. – Красноярск: СТИ, 1982.-36с.

Дата добавления: 2015-08-31