Метод Лагранжа (метод вариации произвольной постоянной)

Метод И. Бернулли

Линейные уравнения. Уравнение Я. Бернулли

Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде

где р(х) и g(x) - заданные функции, в частности - постоянные.

Особенность ДУ (2.11): искомая функция у и ее производная y' входят в уравнение в первой степени, не перемножаясь между собой.

Рассмотрим два метода интегрирования ДУ (2.11) - метод И. Бернулли и метод Лагранжа.

Решение уравнения

ищется с помощью подстановки y=u • v, где u=u(x) и v=v(x) - неизвестные функции от х, причем одна из них произвольна (но не равна нулю).

Действительно любую функцию y(х) можно записать как

где v(x) ≠ 0.

Тогда y'=u'•v+u•v'. Подставляя выражения y и y' в уравнение (2.11), получаем:

u' • v+u • v'+р(х) • u • v=g(x) или

Подберем функцию v=v(x) так, чтобы выражение в скобках было равно нулю, т. е. решим ДУ

v^'+р(х)•v=0. Итак, т.е. Интегрируя, получаем:

Ввиду свободы выбора функции v(x), можно принять с=1. Отсюда

Подставляя найденную функцию v в уравнение (2.12), получаем

Получено уравнение с разделяющимися переменными. Решаем его:

Возвращаясь к переменной υ, получаем решение

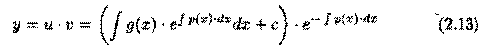
Пример 2.8. Проинтегрировать уравнение y^'+2xy=2х.

Решение: Полагаем у=u•v. Тогда u^'•v+u•v'+2х'•uv=2х, т. е. u' • v+u•(v'+2xv)=2х. Сначала решаем уравнение v'+2х • v=0:

Теперь решаем уравнение

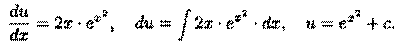
Итак, общее решение данного уравнения есть т. е.

Уравнение интегрируется следующим образом.

Рассмотрим соответствующее уравнение без правой части, т. е. уравнение y'+р(х)•y=0. Оно называется линейным однородным ДУ первого порядка. В этом уравнении переменные делятся:

Таким образом,

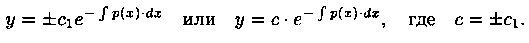
Метод вариации произвольной постоянной состоит в том, что постоянную с в полученном решении заменяем функцией с(х), т. е. полагаем с=с(х). Решение уравнения (2.11) ищем в виде

Находим производную^:

Подставляем значения у и у^' в уравнение (2.11):

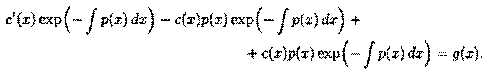
Второе и третье слагаемые взаимно уничтожаются, и уравнение примет вид

Следовательно,

Интегрируя, находим:

Подставляя выражение с(х) в равенство (2.14), получим общее решение ДУ (2.11):

Естественно, та же формула была получена методом Бернулли (ср. с (2.13)).

Пример 2.9. Решить пример 2.8 методом Лагранжа.

Решение: Решаем уравнение Имеем 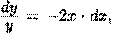или . Заменяем с на с(х), т. е. решение ДУ у^'+2ху=2х ищем в виде . Имеем

Тогда

или или

Поэтому или - общее решение данного уравнения.

Уравнение вида

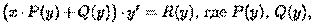
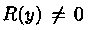- заданные функции, можно свести к линейному, если х считать функцией, а y - аргументом: х=х(у). Тогда, пользуясь равенством

получаем

линейное относительно х уравнение. Его решение ищем в виде х=u•v, где u=u(y), v=v(y) - две неизвестные функции.

Пример 2.10. Найти общее решение уравнения (х+υ)•y'=1.

Решение: Учитывая, что 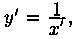от исходного уравнения переходим к линейному уравнению x^'=х+y.

Применим подстановку х=u•v. Тогда 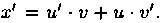Получаем:

или

Находим функцию v:

Находим функцию u:

Интегрируя по частям, находим: u=-y • е^-у - е^-у+с. Значит, общее решение данного уравнения: 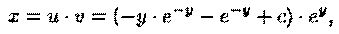или

Дата добавления: 2017-01-13