Методические указания 2 страница

Поясним заполнение симплекс-таблиц. Таблица I. В - строке в столбце записываем скалярное произведение . В остальных столбцах этой строки записываем , 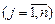. , и т.д.

Для определения вектора вводимого в базис просматриваем - ю строку. В качестве вектора вводимого в базис можно взять любой вектор, для которого . В нашем примере возьмем вектор Р₁ так как он соответствует наименьшему . Столбец, соответствующий вектору Р₁ является направляющим.

Для определения вектора выводимого из базиса находим . Это значение соответствует вектору Р_5, и его будем вывод из базиса. Эта строка является направляющей. Элемент 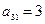является разрешающим элементом. Заполнение таблицы II начинается с заполнения направляющей строки делением всех ее элементов на 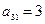. Остальные элементы таблицы II вычисляются по формулам Жордана-Гаусса.

Например, , и т.д.

В таблице II в -ой строке, есть отрицательное . Это . Оно соответствует вектору Р₂ и этот вектор будем вводить в базис. соответствует базисному вектору Р₃ и его будем выводить из базиса. Элемент является разрешающим. Перерасчет элементов таблицы III осуществляется как и раньше. В таблице III в -ой строке среди нет отрицательных, следовательно, получен оптимальный план: , =1140.

Покажем соответствие опорных решений и вершин области допустимых решений. Опорное решение соответствует точке ОДР (области допустимых решений). Опорное решение соответствует точке 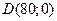. Опорное (оптимальное) решение соответствует точке ОДР.

Симплексный метод с искусственным базисом

Мы рассмотрели симплексный метод для основной задачи линейного программирования у которой среди векторов было ровно единичных векторов. Но во многих ЗЛП записанных в форме основной задачи не всегда есть единичных векторов. В этом случае удобно применять метод искусственного базиса. Пусть требуется найти максимум функции

при условиях

, ,

Среди векторов , , …., 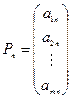нет единичных векторов.

Назовем эту задачу исходной.

Определение. Задача состоящая в нахождении максимума функции

при условиях

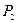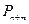и М – некоторое большое положительное число называется расширенной задачей по отношению к исходной задаче. Расширенная задача имеет опорный план Система векторов . , …., имеет ровно единичных векторов ; 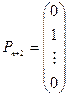, ….., , которые образуют базис -мерного пространства. Этот базис называется искусственным базисом. Переменные называются искусственными. Решение расширенной задачи можно найти симплексным методом. Связь между оптимальными планами исходной и расширенной задач устанавливается следующей теоремой.

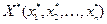Теорема. Если в оптимальном плане расширенной задачи значения всех искусственных переменных равны нулю, т.е. , то план является оптимальным планом исходной задачи.

Решая расширенную задачу симплексным методом, значения и будут состоять из двух слагаемых, одно из которых содержит 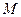, а другое не содержит его. Поэтому для удобства расчетов члены не содержащие 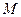записываем в 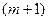-ю строку, а содержащие 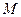в -ю строку. При переходе от одного опорного решения к другому в базис вводится вектор соответствующий наименьшему отрицательному числу в -ой строке. Искусственный вектор исключенный из базиса можно дальше не рассматривать, но если решается двойственная задача, то все искусственные векторы надо сохранять до последней итерации. Итерационный процесс по 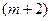-ой строке ведут до тех пор пока:

1) все искусственные векторы не будут исключены из базиса,

2) не все искусственные векторы исключены из базиса, но в 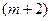-ой строке нет отрицательных элементов в столбцах векторов .

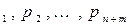В первом случае решение продолжается по -ой строке как и раньше.

Во втором случае, если в 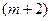-ой строке элемент стоящий в столбце отрицателен, то исходная задача не имеет решения, а если он равен нулю, то найденный опорный план исходной задачи вырожден и базис содержит по крайней мере один из искусственных векторов. Полученный опорный план в общем случае не является оптимальным.

При последующих итерациях в базис вводится вектор стоящий над нулевым элементом 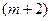-ой строки. Этот процесс продолжается до тех пор пока в -ой строке над нулевыми элементами 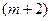-ой строки не останется отрицательных.

Пример.

Решение. Перейдем к основной ЗЛП, введя дополнительные переменные .

Запишем систему ограничений в векторной форме:

,

Здесь ; ; ; ; ; .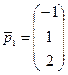

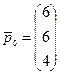Видим, что система векторов имеет только один единичный вектор . Поэтому надо ввести два искусственных вектора и . Расширенная задача имеет вид:

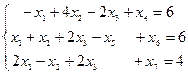, . Решим расширенную задачу табличным методом:

№ табл.

i

базис

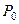
-М

-М

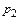
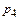
I

P4 P6 P7

-М -М

-1

-1

-2

-1

-

-1

-2

-10

-3

-4

II

P4 P6 P3

-М -1

-1

-1/2

-1

10/3 -

-2

-2

-3/2

-2

-2

III

P4 P2 P3

-1

5/2

5/2 -1/2 3/4

3/2 -1/2 -1/4

14/5 - 10/3

-1/2

-11/4

-3/4

IV

P1 P2 P3

-1

14/5 12/5 2/5

2/5 1/5 -3/10

3/5 -1/5 -7/10

7,2

11/10

9/10

Так как среди 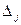в последней таблице нет отрицательных, то получен оптимальный план расширенной задачи , .

Поскольку в этом плане все искусственные переменные равны нулю, то план является оптимальным планом исходной задачи. Итак, , .

Двойственные задачи линейного программирования

Каждой ЗЛП можно определенным образом сопоставить некоторую другую ЗЛП называемую двойственной или сопряженной по отношению к исходной или прямой задаче. Обычно двойственные задачи подразделяются на симметричные и несимметричные. Рассмотрим двойственные симметричные задачи.

Исходная (прямая) задача. Найти максимальное значение функции

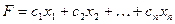
при условиях

Соответствующая двойственная ЗЛП состоит в нахождении минимального значения функции

при условиях

Деление пары задач на исходную и двойственную условно, т.е. задача нахождения минимального значения функции может считаться исходной, а задача нахождения максимального значения функции считаться двойственной.

Замечание. Для пары двойственных симметричных задач обязательно требование неотрицательности переменных и .

Пример. Составить двойственную задачу к заданной.

Исходная задача: найти максимальное значение функции 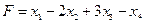. При условиях: ,

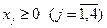
Решение. Двойственная задача: найти минимальное значение функции 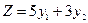при условиях: , .

Дадим определение двойственной задачи к общей задаче линейного программирования.

Исходная задача. Требуется найти максимальное значение функции при условиях:

Двойственная задача. Найти минимальное значение функции при условиях:

Выпишем основные правила составления двойственной задачи.

1. Если целевая функция исходной задачи исследуется на максимум, то целевая функция двойственной задачи исследуется на минимум и наоборот.

2. Если матрица из коэффициентов при неизвестных в системе ограничений исходной задачи, то матрицей из коэффициентов при неизвестных двойственной задачи являются ей транспонированная матрица .

3. Число переменных в двойственной задаче равно числу ограничений в исходной задаче, а число ограничений в двойственной задаче равно числу переменных в исходной задаче.

4. Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а свободными членами в системе ограничений двойственной задачи являются коэффициенты при неизвестных в целевой функции исходной задачи.

5. Если переменная исходной задачи неотрицательна, то ое условие в системе ограничений двойственной задачи есть неравенство вида , если целевая функция исследуется на минимум или 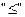, если целевая функция исследуется на максимум, а если принимает любые значения, то ое условие есть равенство. Аналогично, если ое условие в системе ограничений исходной задачи есть неравенство, то 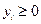, а если ое условие – равенство, то может принимать любые значения.

Пример. Исходная задача:

.

Двойственная задача:

.

Каждой из пары двойственных задач являются самостоятельными ЗЛП и могут решаться независимо одна от другой. Однако, их решения связаны между собой и, зная оптимальное решение одной из них, можно указать оптимальное решение другой. Связь между решениями прямой и двойственной задач устанавливается двумя теоремами двойственности.

Теорема 1. Если одна из пары двойственных задач имеет оптимальный план , то и вторая имеет оптимальный план , причем . Если же целевая функция одной из задач неограниченна, то другая вообще не имеет планов.

Теорема 2. План исходной задачи и план 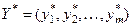являются оптимальными планами тогда и только тогда, когда для любого выполняется равенство: .

То есть всякий раз, когда ое ограничение двойственной задачи при подстановке оптимального плана обращается в строгое неравенство, ая переменная исходной задачи равна нулю. Если ая переменная двойственной задачи положительна, то ое ограничение исходной задачи есть строгое равенство.

Рассмотрим применение этой теоремы на примере решения задачи 1.

Исходная задача:

Двойственная задача:

.

Ранее было найдено оптимальное решение , .

При подстановке этого решения в систему ограничений исходной задачи видим, что второе ограничение обращается в строгое неравенство следовательно, двойственная переменная . Так как и положительны, то первое и второе ограничения двойственной задачи есть строгие равенства: .

А так как , то имеем систему уравнений . Решая эту систему, получим: , 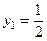. Таким образом, оптимальный план двойственной задачи будет . . Видим, что

Замечание. Решение двойственной задачи можно найти также исходя из решения исходной задачи табличным симплексным методом.

Справедлива теорема: Пусть симплексным методом найден оптимальный план исходной задачи и этот план определяется базисом: , где - номер последней симплекс-таблицы. И пусть - вектор-строка из коэффициентов при неизвестных целевой функции, соответствующая этому базису. Тогда оптимальный план двойственной задачи будет , где матрица - матрица обратная матрице , составленной из компонент векторов 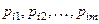взятых из первой симплекс-таблицы.

Дата добавления: 2017-01-13