Азбука теории графов. Маршрут, путь, простой путь. Цикл. Простой цикл. Связность в графе

Задание графа с помощью списка смежности.

Задание графа с помощью матрицы инцидентности.

Задание графа с помощью матрицы смежности.

Представление графов

Пусть в графе число вершин равно :

Для задания графа будем использовать квадратную матрицу размера 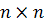. Каждая строка и каждый столбец матрицы соответствуют определенной вершине графа. На пересечении строки 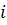и столбца 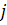ставим 1 тогда и только тогда, когда неупорядоченная пара является ребром графа. В противном случае ставим 0. Таким образом, число единиц в матрице определяется числом ребер графа. Матрица смежности неориентированного графа является симметрической (т.е. она совпадает со своей транспонированной матрицей).

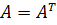
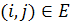
Действительно, если пара – ребро графа, тогда пара 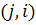также является ребром графа (так как рассматривается неориентированный граф).

Пусть задан граф с вершинами и ребрами:

,

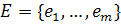
Матрица инцидентности для данного графа есть прямоугольная матрица размера размера , строки матрицы соответствуют вершинам, столбцы – ребрам.

На пресечении строки 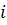и столбца 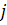ставим 1 тогда и только тогда, когда вершина 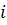является одним из концов ребра 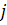, в противном случае – 0. Таким образом, каждый столбец матрицы инцидентности содержит либо две единицы, либо одну. Если столбец содержит одну единицу, то ребро, соответствующее данному столбцу, является петлей.

Для каждой вершины выписывается множество вершин, которые смежны с рассматриваемой. Вершина 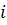смежна с вершиной 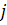, если – ребро графа. Данный способ является наиболее экономным способом представления графов.

Определение. Полным графом называется граф, в котором все вершины соединены между собой неориентированными ребрами. То есть, множество ребер состоит из всевозможных неупорядоченных пар вершин графа. Число вершин графа (мощность множества вершин графа) будем обозначать 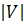. Число ребер в полном неориентированном графе на множестве вершин V задается формулой 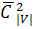. Если 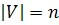, тогда:

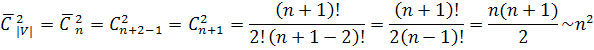
То есть, по порядку, число вершин в полном графе квадратично относительно мощности множества вершин 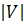графа. Размер матрицы смежности неориентированного графа – . Общая память квадратична по , что является неэкономичным, когда граф разряжен, то есть число ребер мало.

Пример. Рассмотрим пустой граф на множестве вершин и пустом множестве ребер :

,

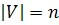
тогда матрица смежности потребует 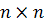памяти, а список смежности будет содержать только перечисление вершин графа, поэтому память будет линейна относительно .

Аналогичным образом можно представлять ориентированные графы. Отличие будет в представлении матрицы инцидентности и списка смежности. В матрице инцидентности будем ставить 1 на пересечении строки 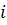и столбца 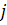, если вершина 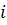является началом некоторого ребра, а врешина 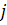– концом данного ребра и -1 будем ставить, если вершина 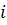является концом некоторого ребра, а вершина 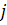– его началом. Если нет ребра, соединяющего вершины 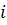и 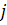, то ставим 0.

В списке смежности для вершины 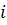выписываем вершины концов ребер, исходящих из вершины .

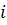Определение. Два графа называются изоморфными, если между вершинами графов можно установить взаимооднозначное соответствие , сохраняющее соответствие смежности между вершинами.

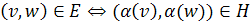
Иначе говоря, графы изоморфны, если они одинаковы с точностью до переименования вершин.

Пример. Представленная пара графов изоморфна:

~

Изоморфизм определяется следующим соотношением между вершинами:

Следующие два графа не изоморфны:

Очевидно, что изоморфные графы должны иметь одно и то же число вершин и одно и то же число ребер. В представленных графах число ребер различно.

Определение изоморфности ориентированных графов аналогично.

Определение. Маршрутом 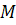в графе называется последовательность вершин 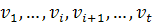, где пара соседних вершин 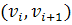является ребром графа.

-1

В этом случае будем говорить, что маршрут M соединяет вершины .

Пример.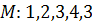

Определение. Путем, соединяющим пару вершин будем называть маршрут, соединяющий данную пару вершин и не содержащий повторяющихся ребер.

Определение. Простым путем, соединяющим пару вершин будем называть путь, соединяющий данную пару и не содержащий повторяющихся вершин.

Определение. Пару вершин в графе будем называть связной, если либо вершины совпадают, либо существует маршрут, соединяющий две эти вершины.

Пример. Любая пара вершин в следующем графе связана:

В следующем графе связанными являются не все вершины:

Вершины 1 и 2 связаны, а, например, вершины 2 и 3 не связаны.

Утверждение. Если в графе существует маршрут, соединяющий пару вершин, то существует простой путь, который соединяет данную пару вершин.

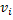
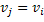
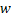
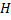
Рассмотрим маршрут, соединяющий вершины . Предположим, что вершина повторяется на маршруте. Тогда вырежем участок маршрута 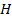между повторяющимися вершинами и соединим полученные части. Данную операцию будем повторять до тех пор, пока в маршруте не будет повторяющихся вершин.

Таким образом, получен простой путь, соединяющий пару вершин . Поэтому для связности вершин достаточно наличие простого пути, который их соединяет.

Определение. Циклом называется путь, в котором начальная и конечная врешины совпадают.

Пример.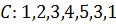

Определение. Простым циклом называется путь, в котором вершины не повторяются, за исключением первой и последней. Другими словами, простой цикл - это цикл без самопересечения.

Пример. Простой цикл: .

Дата добавления: 2017-01-13