Методика выбора аппроксимирующей функции

Аппроксимирующую функцию 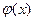выбирают из некоторого семейства функций, для которого задан вид функции, но остаются неопределенными (и подлежат определению) её параметры 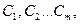т.е.

Определение аппроксимирующей функции φ разделяется на два основных этапа:

1. Подбор подходящего вида функции ;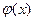

2. Нахождение ее параметров в соответствии с критерием МНК.

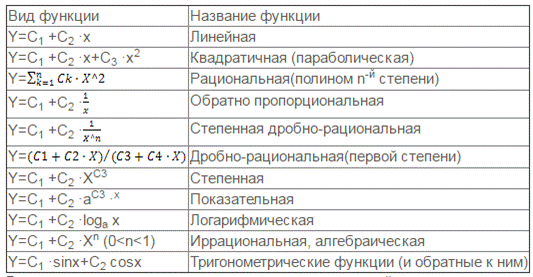
Подбор вида функции 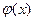представляет собой сложную задачу, решаемую методом проб и последовательных приближений. Исходные данные, представленные в графической форме (семейства точек или кривые), сопоставляется с семейством графиков ряда типовых функций, используемых обычно для целей аппроксимации. Некоторые типы функций 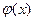, используемых в курсовой работе, приведены в таблице ниже.

Более подробные сведения о поведении функций, которые могут быть использованы в задачах аппроксимации, можно найти в справочной литературе. В большинстве заданий вид аппроксимирующей функции 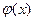уже задан.

Рассмотрим случай многочлена 2-ой степени:

Рассмотрим аппроксимирующую функцию в виде квадратичной функции, соответственно ищем квадрат разности между экспериментальными данными и нашей аналитической функцией с неизвестными коэффициентами.

Где a0, а1, а2 – параметры аппроксимирующей функции;

n – объем выборки;

x ﺂ - номер периода от 1 до n;

y ﺂ - значение показателя Y в момент времени ﺂ.

Далее находим частные производные и приравниваем их к нулю, так как функция будет иметь минимум только в этом случае

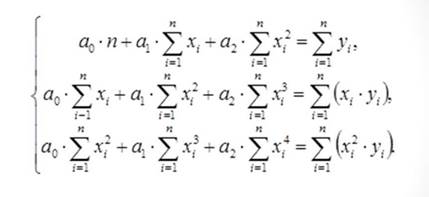После преобразований получаем:

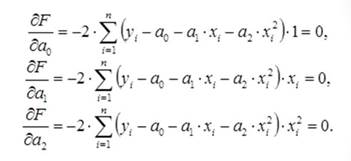
Затем решаем систем методом Крамера (кстати, ее можно решить и другими методами. Например, нам известен метод обратной матрицы и метод Гаусса – результат будет один и тот же). Распишем решение системы методом Крамера и пример.

Возвращаясь к полученной системе уравнений, введем обозначения, которые упростят ход решения (путем замены переменных мы сведем данный полином к линейной функции):

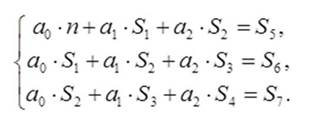С учетом изменений система уравнений будет выглядеть так:

Решим ее методом Крамера, для этого найдем определитель всей системы, а затем, по порядку, найдем дельты каждых неизвестных коэффициентов:

1. Определитель

2. Определитель для a0:

3. Определитель для a1:

4. Определитель для а2:

Пример. Дана табличная зависимость y от x. Построить аппроксимирующий полином в виде y=a0+a1*x+a2*x^2

Дата добавления: 2017-01-13