Расчет термодинамических характеристик гальванических элементов

Так как

Электрическая проводимость растворов электролитов

Мерой способности веществ проводить электрический ток является эл ектрическая проводимость (L) – величина обратная электрическому сопротивлению проводника R:

. (3.15)

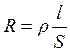, (3.16)

то

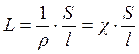, (3.17)

где ρ – удельное сопротивление, Ом·м (Ом·см);

S – поперечное сечение проводника, м² (см²);

– длина проводника, м (см);

– удельная электрическая проводимость, Ом^-1·м^-1 (Ом^-1·см^-1).

Удельная электрическая проводимость (χ – каппа) раствора – это электрическая проводимость объема раствора, заключенного между двумя параллельными электродами, имеющими площадь по 1м² (1 см²) и расположенными на расстоянии 1м (1 см) друг от друга.

Сопротивление раствора связано с удельной электрической проводимостью соотношением:

, 3.18)

где l – расстояние между электродами, S – поверхность электродов; – постоянная измерительной ячейки.

Если известна величина К, то по измеренному в данной ячейке сопротивлению раствора можно рассчитать значение удельной электрической проводимости:

(3.19)

Постоянная измерительной ячейки К может быть найдена путем измерения в данной ячейке сопротивления (R_{ст .}) электролита с известной удельной электрической проводимостью () и расчета по следующей формуле:

К = R_ст ∙ (3.20)

Эквивалентная (мольная) электрическая проводимость λ_v численно равна электрической проводимости такого объема V (м³, л, см³) раствора данной концентрации, в котором содержится 1г-экв (1 моль) растворенного вещества. Условно, это электрическая проводимость объема V раствора, заключенного между двумя параллельными электродами, с расстоянием между электродами 1м (1 см) и такой поверхностью, чтобы между электродами поместился объем раствора данной концетрации, в котором содержится 1г-экв (1моль) электролита.

Эквивалентная (мольная) электрическая проводимость и удельная электрическая проводимость связаны соотношением:

. (3.21)

Если концентрация выражена в г-экв/л (моль/л), а удельная электрическая проводимость в Ом^-1 · см^-1, то

, (3.22)

или с учетом (3.5):

. (3.23)

Эквивалентная электрическая проводимость при бесконечном разбавлении () в соответствии с законом Кольрауша (законом независимого движения ионов) равна:

, (3.24)

где 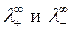– эквивалентные электрические проводимости (электрические подвижности) катиона и аниона при бесконечном разведении; их значения приводятся в справочниках.

Степень диссоциации слабого электролита α и коэффициент электрической проводимости растворов сильных электролитов f (характеризует степень межионного взаимодействия) могут быть рассчитаны по формулам:

(3.25)

(3.26)

П р и м е р 3.4. Какой объем раствора электролита нормальной концентрации C_N = 0,5 г-экв/л нужно условно залить в ячейку с электродами, расстояние между которыми 1 см, чтобы измеренная электропроводность была эквивалентной электропроводностью этого раствора?

Р е ш е н и е

Эквивалентная электропроводность – это электропроводность объема раствора, содержащего 1 г-экв электролита. В 1 л исходного раствора содержится 0,5 г-экв, поэтому

V = 1 /C_N = 1/0,5 = 2 л/г-экв,

то есть следует условно залить 2 л раствора, чтобы в нем находилось нужное количество электролита – 1 г-экв..

П р и м е р 3.5. Рассчитать удельную и эквивалентную электрические проводимости раствора хлорида калия KCl с концентрацией 0,02 г-экв/л, если удельное сопротивление ρ составляет 354,61 Ом·см.

Р е ш е н и е

Найдем удельную электрическую проводимость:

Определим эквивалентную электрическую проводимость:

П р и м е р 3.6. Рассчитать эквивалентную электрическую проводимость раствора концентрации 0,075 г-экв/л, помещенного в ячейку с расстоянием между электродами 1,2 см и поверхностью каждого электрода 0,8 см², если сопротивление раствора составляет 950 Ом.

Р е ш е н и е

Сопротивление раствора:

;

отсюда удельная электрическая проводимость:

;

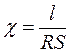Ом^-1· см^-1 Ом^-1· м^-1.

Зная , рассчитываем эквивалентную электрическую проводимость:

;

;

П р и м е р 3.7. Определить постоянную измерительной ячейки K, если раствор концентрации 0,005 г-экв/л имеет эквивалентную электрическую проводимость 400 Ом^-1 ·г-экв^–1 ·см², а сопротивление этого раствора составляет 290 Ом.

Р е ш е н и е

Находим удельную электрическую проводимость раствора:

Сопротивление раствора:

,

отсюда

;

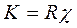см^-1.

П р и м е р 3.8. Сопротивление раствора концентрации 0,015 г-экв/л составляет 1800 Ом. Постоянная измерительной ячейки равна 2,5 см^-1. Рассчитать эквивалентную электрическую проводимость раствора.

Р е ш е н и е

По уравнению (3.19):

Находим эквивалентную электрическую проводимость:

П р и м е р 3.9. Определить степень диссоциации и константу диссоциации одно-одновалентного слабого электролита, если при разведении V = 16 л удельная электрическая проводимость раствора составляет 1,312·10^-3 Ом^-1см^-1, а 232,6 Ом^-1см²/г-экв.

Р е ш е н и е

Находим эквивалентную электрическую проводимость по уравнению (3.23):

;

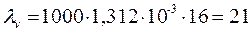Ом^-1см²/г-экв.

Находим степень диссоциации электролита по формуле (3.25):

Рассчитываем константу диссоциации по уравнению Оствальда (3.6):

г-экв/л

П р и м е р 3.10. Определить количество AgCl (г), содержащегося в 1 л раствора, если удельная электрическая проводимость насыщенного водного раствора AgCl составляет 1,259·10^-6 Ом^-1см^-1. Подвижности ионов: Ом^-1см²/г-ион; Ом^-1см²/г-ион.

Р е ш е н и е

Так как хлорид серебра является малорастворимым соединением, то

Из уравнения:

,

может быть выражена концентрация раствора:

или в г/л:

где 143,38 – эквивалент хлорида серебра, равный его молярной массе.

Гальванические элементы – это устройства, позволяющие получать постоянный электрический ток за счет окислительно-восстановительных химических реакций. Гальванический элемент состоит из двух электродов с различными электрическими потенциалами, возникающими на границе раздела твердой фазы (чаще всего металла) и жидкой фазы (раствора электролита). На одном из электродов происходит реакция восстановления (присоединение электронов), на другом – реакция окисления (отдача электронов). Например, в медно-цинковом гальваническом элементе Якоби-Даниэля на цинковом электроде, помещенном в раствор своей соли (например, ZnSO₄), протекает процесс окисления цинка:

Zn ↔ Zn²⁺ + 2e^-, (3.27)

на медном электроде, помещенном в раствор своей соли (например, CuSO₄) – процесс восстановления ионов меди:

Cu²⁺ + 2e^- ↔ Cu. (3.28)

Эти процессы пространственно разделены. Суммарная химическая реакция, за счет которой получается электрический ток в этом элементе:

Zn + Cu²⁺ ↔ Zn²⁺ + Cu. (3.29)

Эта химическая окислительно-восстановительная реакция является гетерогенной, поэтому константа равновесия для нее может быть записана следующим образом:

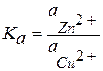, (3.30)

где 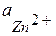и - активности потенциалопределяющих ионов Zn²⁺ и Cu²⁺ в растворах полуэлементов.

Гальванический элемент записывается таким образом, чтобы электрод, на котором происходит окисление (более электроотрицательный), находился слева. Например, медно-цинковый гальванический элемент может быть записан следующим образом:

Zn ê ZnSO₄ êê CuSO₄ ê Cu. (3.31)

Абсолютные значения потенциалов электродов неизвестны. Условные относительные потенциалы электродов (электродные потенциалы) рассчитываются по уравнению Нернста, которое в общем случае можно записать следующим образом:

, (3.32)

где – активность окисленной формы потенциалопределяющих (участвующих в электродных реакциях) ионов; 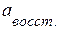– активность восстановленной формы; z – количество электронов, участвующих в одном акте электродной реакции (для реакции (3.29) z =2); R – универсальная газовая постоянная (8,314 Дж/(моль·К)); F = 96485 ~ 96500 Кл/г-экв – постоянная Фарадея; – стандартный электродный потенциал.

Если электрод представляет собой металл, опущенный в раствор своей соли, то:

. (3.33)

Так как активность чистых индивидуальных веществ (в данном случае, металла) равна 1, то уравнение для электродного потенциала электрода может быть записано в следующем виде:

, (3.34)

Стандартный электродный потенциал φ^о характеризует потенциал электрода при активностях потенциалопределяющих ионов, равных 1. Значения стандартных электродных потенциалов (соответствующих электродных реакций, записанных как реакции восстановления), приводятся в справочной таблице стандартных потенциалов (табл. 7.4). Они определены по отношению к стандартному водородному электроду, потенциал которого в выбранных стандартных условиях принят равным 0.

Электродвижущая сила ( ЭДС ) гальванического элемента (Е) – величина положительная и определяется как разность потенциалов положительного и отрицательного электродов:

Е = j₍₊₎ – j_(–). (3.35)

Для рассмотренного гальванического элемента:

. (3.36)

Электродвижущая сила (ЭДС) гальванического элемента может быть рассчитана по уравнению Нернста:

, (3.37)

где и – активности потенциалобразующих ионов положительного и отрицательного электродов;

E⁰ – стандартная электродвижущая сила гальванического элемента – это ЭДС гальванического элемента при активностях потенциалобразующих ионов положительного и отрицательного электрода или их отношении, равных единице. Стандартная ЭДС равна разности стандартных электродных потенциалов положительного и отрицательного электродов:

. (3.38)

Дата добавления: 2017-01-14