
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Явление электромагнитной индукции. Закон Фарадея – Максвелла. Правило Ленца
|
|
|
|
Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
Закон Фарадея
Согласно закону электромагнитной индукции Фарадея (в СИ):
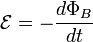
где
 —электродвижущая сила, действующая вдоль произвольно выбранного контура,
—электродвижущая сила, действующая вдоль произвольно выбранного контура,

 — магнитный поток через поверхность, натянутую на этот контур.
— магнитный поток через поверхность, натянутую на этот контур.
Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:
Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

где
 — электродвижущая сила,
— электродвижущая сила,
 — число витков,
— число витков,
 — магнитный поток через один виток,
— магнитный поток через один виток,
 — потокосцепление катушки.
— потокосцепление катушки.
Векторная форма
В дифференциальной форме закон Фарадея можно записать в следующем виде:
 (в системе СИ)
(в системе СИ)
или
В интегральной форме (эквивалентной):
 (СИ)
(СИ)
или
Здесь  — напряжённость электрического поля,
— напряжённость электрического поля, 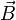 — магнитная индукция,
— магнитная индукция,  — произвольная поверхность,
— произвольная поверхность,  — её граница. Контур интегрирования
— её граница. Контур интегрирования  подразумевается фиксированным (неподвижным).
подразумевается фиксированным (неподвижным).
Если же, скажем, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенство  продолжает соблюдаться, но ЭДС в левой части теперь не сводится к
продолжает соблюдаться, но ЭДС в левой части теперь не сводится к  (которое в данном частном примере вообще равно нулю). В общем случае (когда и магнитное поле меняется со временем, и контур движется или меняет форму) последняя формула верна так же, но ЭДС в левой части в таком случае есть сумма обоих слагаемых, упомянутых выше (то есть порождается частично вихревым электрическим полем, а частично силой Лоренца и силой реакции движущегося проводника).
(которое в данном частном примере вообще равно нулю). В общем случае (когда и магнитное поле меняется со временем, и контур движется или меняет форму) последняя формула верна так же, но ЭДС в левой части в таком случае есть сумма обоих слагаемых, упомянутых выше (то есть порождается частично вихревым электрическим полем, а частично силой Лоренца и силой реакции движущегося проводника).
|
|
|
Уравнение Фарадея — Максвелла
Переменное магнитное поле создаёт электрическое поле, описываемое уравнением Фарадея — Максвелла:
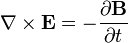
|
где:
 обозначает ротор
обозначает ротор
E — электрическое поле
B — плотность магнитного потока.
Это уравнение присутствует в современной системе уравнений Максвелла, часто его называют законом Фарадея. Однако, поскольку оно содержит только частные производные по времени, его применение ограничено ситуациями, когда заряд покоится в переменном по времени магнитном поле. Оно не учитывает электромагнитную индукцию в случаях, когда заряженная частица движется в магнитном поле.
В другом виде закон Фарадея может быть записан через интегральную форму теоремы Кельвина-Стокса:

Для выполнения интегрирования требуется независимая от времени поверхность Σ (рассматриваемая в данном контексте как часть интерпретации частных производных). Как показано на рис. 6:
Σ — поверхность, ограниченная замкнутым контуром ∂Σ, причём, как Σ, так и ∂Σ являются фиксированными, не зависящими от времени,
E — электрическое поле,
dℓ — бесконечно малый элемент контура ∂Σ,
B — магнитное поле,
dA — бесконечно малый элемент вектора поверхности Σ.
|
|
|
Правило Ленца определяет направление индукционного тока и гласит:
Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.
Физическая суть правила.
Согласно закону электромагнитной индукции Фарадея при изменении магнитного потока 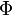 , пронизывающего электрический контур, в нём возбуждается ток, называемый индукционным. Величина электродвижущей силы, ответственной за этот ток, определяется уравнением:
, пронизывающего электрический контур, в нём возбуждается ток, называемый индукционным. Величина электродвижущей силы, ответственной за этот ток, определяется уравнением:

где знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт и отражён в правиле Ленца.
Правило Ленца носит обобщённый характер и справедливо в различных физических ситуациях, которые могут отличаться конкретным физическим механизмом возбуждения индукционного тока.
Билет 7
1.В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.
P(вектор)=Р1+Р2+…Рn
Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выполняется и для замкнутых систем микрочастиц. Этот закон носит универсальный характер.
2. Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока. При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС. 
Индукти́вность(ед.измерения Генри) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур.
Взаимоиндукция — возникновение ЭДС в одном проводнике вследствие изменения силы тока в другом или вследствие изменения взаимного расположения проводников. Направление тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Правило указывает на то, что изменение тока в одной цепи (катушке) встречает противодействие со стороны другой цепи (катушки).Чем большая часть магнитного поля первой цепи пронизывает вторую цепь, тем сильнее взаимоиндукция между цепями. С количественной стороны явление взаимоиндукции характеризуется коэффициентом взаимоиндукции(L)
|
|
|
БИЛЕТ 8
1. Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени. Для замкнутой системы тел момент внешних сил всегда равен нулю, так как внешние силы вообще не действуют на замкнутую систему.
Поэтому  , то есть
, то есть 
2. Энергия магнитного поля равна работе, которая затрачивается током на создание этого поля. Рассмотрим контур индуктивностью L, по которому течет ток I. работа по созданию магнитного потока Ф будет равна
 Энергия магнитного поля, связанного с контуром,
Энергия магнитного поля, связанного с контуром, 
Однородное магнитное поле внутри длинного соленоида. Энергия  Так как I = Bl/
Так как I = Bl/  и B=
и B= 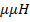 , то
, то  Sl = V-объем соленоида. Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью
Sl = V-объем соленоида. Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью

|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 5611; Нарушение авторских прав?; Мы поможем в написании вашей работы!