Кибиткин В.В., Солодушкин А.И., Плешанов В.С

АЛГОРИТМ ВЫДЕЛЕНИЯ ВИХРЕВЫХ СТРУКТУР В ДЕФОРМИРУЕМОМ МАТЕРИАЛЕ

ВЛИЯНИЕ РЕЖИМА ДЕФОРМАЦИИ КРУЧЕНИЕМ ПОД ДАВЛЕНИЕМ НА ТЕКСТУРУ ВТСП КЕРАМИКИ Bi(Pb)2223

Пархимович Н.Ю. 1, Имаев М.Ф. 1,2

1Институт проблем сверхпластичности металлов РАН, Уфа

2 Башкирский государственный университет, Уфа

[e-mail]

Керамика Bi(Pb)2Sr2Ca2Cu3O10 {Bi(Pb)2223}, благодаря своей нетоксичности и высокой температуре сверхпроводящего перехода (T с = 105–110 K) перспективна для практического применения как в качестве лент и проводов, так и в виде объем- ных изделий. Из Bi(Pb)2223 могут быть изготовлены магнитные подшипники, на- копители энергии, компактные ограничители тока короткого замыкания в электри- ческих цепях, моторы и генераторы с высоким КПД и низким уровнем шума.

Плотность транспортного критического тока сильно зависит от разориенти- ровки зерен, поэтому для достижения высоких сверхпроводящих свойств необхо- димо получить острую текстуру. В то время как провода и ленты получают мето- дом «порошок в трубе» в сочетании с одноосным сжатием, для получения тексту-

рованного объемного материала целесообразно применять горячую деформацию методом кручения под квазигидростатическим давлением [1,2].

В данной работе образцы Bi(Pb)2223 в форме таблеток подвергали деформа- ции кручением под давлением на машине сложного нагружения. Условия дефор- мации следующие: осевая нагрузка 2500 Н, интервал температур деформации 855– 930oС, интервал скоростей кручения 4–17х10-4 об/мин, интервал углов кручения 5– 90о.

Обнаружено, что режим деформации оказывает сильное влияние на размер колоний зерен, фазовый состав и текстуру керамики. Деформация в метастабиль- ной области температур (Т > 870оС) сопровождается выделением мелких частиц вторичных фаз в результате частичного распада матричной фазы Bi(Pb)2223. Про- веден качественный и количественный анализ формирующихся частиц. Установ-

лено, что максимум текстуры формируется в метастабильной температурной об- ласти. Исследовано влияние скорости кручения на параметры структуры и тексту- ру керамики Bi(Pb)2223.

1. Imayev M.F., Daminov R.R., Reissner M., Steiner W., Makarova M.V., Kazin P.E. Microstructure, texture and superconducting properties of Bi2212 ceramics, deformed by torsion under pressure // Physica C. 2007. Vol. 467. P. 14-26.

2. Имаев М.Ф., Кабирова Д.Б. Формирование базисной текстуры при горячей деформа- ции ВТСП керамики YBa2Cu3O7-x // Перспективные материалы. 2009. Вып.7. С. 124- 129.

Институт физики прочности и материаловедения СО РАН, Томск, Россия

[e-mail]

Исследование пластического течения материала при механическом воздейст- вии характеризуется векторным полем необратимых смещений. Хотя поведение твёрдого деформируемого тела отличается от поведения жидкости или газа, в нём также могут формироваться и развиваться вихревые структуры. Метод корреляции цифровых изображений (КЦИ) позволяет эффективно исследовать неоднородности деформации материала и её эволюцию.

Вихрем будем считать такой характер плоского течения, когда вектор смеще- ния нормален своему радиус-вектору, проведённому из его центра, а циркуляция по линиям тока отлична от нуля. Этому определению соответствует условие x ¢ u x + y ¢ u y = 0, где x ¢, y ¢ - координаты радиус-вектора в локальной системе координат X¢OY¢, ux, uy - проекции вектора. При обработке данных эксперимента возникает задача идентификации этого вихря, определения его размеров и центра.

Моделирование было выполнено на примере вихревого поля с постоянной

...

амплитудой u 0, имеющего вид

полярной системе координат.

u = u 0 ej, где ej - тангенциальный орт в локальной

Для поиска центра вихря выполнялось сканирование в пределах всего век- торного поля с глобальной системой координат XOY квадратными участками раз-

мером R ´ R. В каждом текущем положении (i, j) в пределах участка рассчитывались значения функционала d, который имеет вид

R R

di, j =

|{åå[ x '(i ') × uxi, j (i ', j ') + y '× uyi, j (i ', j ')]}|.

i '=1 j '=1

На рисунке приведено его пространственное распределение. Видно, что су- ществует область с минимальными значениями функционала, которая имеет вид наклонного отрезка. Размер этого отрезка равен диаметру вихря, а его середина со- ответствует координатам центра вихря. Угол наклона отрезка определяется на- правлением вращения.

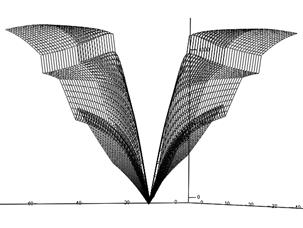
Рис. Пространственное распределение функ- ционала d. R = 15, u 0 = 1

Использование модуля позво- ляет свести задачу к поиску экстре- мума. Значения функционала, от- личные от минимального, связаны с тем, что радиус-вектор отсчитыва- ется не от центра вращения. Легко также показать, что постоянная со- ставляющая векторного поля до- бавляет некоторую константу к значению функционала и поэтому не влияет на его работу.

Данный подход имеет общий характер, не зависит от других ха- рактеристик вихря и показал свою работоспособность для векторных полей, полученных методом КЦИ.

Дата добавления: 2017-01-14