
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тура жол алгоритмі 9 страница
|
|
|
|

өрнегінде барлық 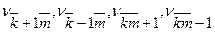 және
және  шамаларын
шамаларын  санымен алмастырайық. Сонда теореманың шартына сәйкес
санымен алмастырайық. Сонда теореманың шартына сәйкес
 (25)
(25)
теңсіздігін аламыз. Алайда, 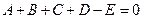 . Ендеше (25) теңсіздігінен
. Ендеше (25) теңсіздігінен  деген тұжырымға келеміз. Ал шекаралық есептің шарты бойынша
деген тұжырымға келеміз. Ал шекаралық есептің шарты бойынша  . Бүл қарама-қайшылық жоғарыдағы ұйғарымның дүрыс еместігін көрсетеді. Теорема дәлелденді.
. Бүл қарама-қайшылық жоғарыдағы ұйғарымның дүрыс еместігін көрсетеді. Теорема дәлелденді.
Дәл осы жолмен мына теореманы да дәлелдеуге болады.
Теорема-2. Егер қандай да бір  торлық функция үшін
торлық функция үшін  ішкі тораптарында
ішкі тораптарында  болса, онда
болса, онда  функциясы
функциясы  -да теріс минимумға ие бола алмайды.
-да теріс минимумға ие бола алмайды.
Бұл екі теоремадан мынадай маңызды қорытынды шығарамыз: (19)-(20) айырымды шекаралық есебінің  шешімі өзінің ең үлкен және ең кіші мәндеріне тек қана шекаралық тораптарда ғана ие бола алады.
шешімі өзінің ең үлкен және ең кіші мәндеріне тек қана шекаралық тораптарда ғана ие бола алады.
Енді 1 және 2 –теоремаларын пайдаланып, (21)-(22) айырымдық есебінің бір ғана шешімі бар болатындығын дәлелдейміз. Ол үшін (21)-(22) жүйесіне сәйкес келетін
 (26)
(26)
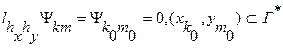 (27)
(27)
біртекті жүйенің тек  шешімі бар екендігін дәлелдесек жеткілікті. Бұл тұжырым 1 және 2 теоремаларында дәлелденген принциптерден келіп шығады. Шынында да, егер (26)-(27) біртекті теңдеуінің қандай да бір
шешімі бар екендігін дәлелдесек жеткілікті. Бұл тұжырым 1 және 2 теоремаларында дәлелденген принциптерден келіп шығады. Шынында да, егер (26)-(27) біртекті теңдеуінің қандай да бір  ішкі торабында
ішкі торабында  шешімі бар болса, онда
шешімі бар болса, онда  болғандықтан, 1 және 2 –теоремалары бойынша
болғандықтан, 1 және 2 –теоремалары бойынша  функциясы өзінің ең үлкен оң немесе ең кіші теріс мәндеріне
функциясы өзінің ең үлкен оң немесе ең кіші теріс мәндеріне  -да ие болуы тиіс. Алайда,
-да ие болуы тиіс. Алайда,  -да
-да  . Сондықтан бола алмайды. Демек, (24)-(27) біртекті жүйесінің шешімі тек
. Сондықтан бола алмайды. Демек, (24)-(27) біртекті жүйесінің шешімі тек  болады.Ендеше(21)-(22) есебінің бір ғана шешімі бар.
болады.Ендеше(21)-(22) есебінің бір ғана шешімі бар.
Дәл осыған ұқсас жолдармен Нейман және Ньютон есептерін жуықтайтын айырымдық схемалардың да бір ғана шешімдері бар болатындығы дәлелденеді.
|
|
|
13-ДӘРІС. Эллиптикалық теңдеу.
1. Пуассон теңдеуі үшін Дирихле есебіне сәйкес келетін айырымдық есеп, оған максимум принципі.
Ыдырату әдісінің негізінде қуалау әдісін пайдаланып итерацияны жүзеге асыру алгоритмі
1.3. Пуассон теңдеуі қойылған Дирихле есебі.
Пуассон теңдеуі-эллипстік теңдеулердің ішіндегі жан-жақты зерттелген теңдеулерінің бірі. Оған үш түрлі шекаралық есептер қоюға болады. Солардың негізгісі-Дирихле есебі болып табылады.
1.3.1. Дирихле есебін жуықтату
Дифференциалдық теңдеулер теориясында мынадай теңдеу
 (28)
(28)
Пуассон теңдеуі деп аталады. Дирихле есебі бойынша (28)теңдеуінің  (
( -ішкі облыс,
-ішкі облыс,  -шекаралық облыс) облысында әрі анықталған, әрі үзіліссіз, ал Г-да
-шекаралық облыс) облысында әрі анықталған, әрі үзіліссіз, ал Г-да
 (29)
(29)
берілген мәнін қабылдайтын  шешімі ізделеді.Мұндай есеп математикалық физика теңдеулер теориясында кеңінен зерттелген. Оның әр түрлі координаттар жүйесіндегі шешімдері және олардың есептеу формулалары да анықталған. Алайда бұл формулалар есептеуге өте қолайсыз. Сондықтан да Дирихле есебін шешу үшін көбінесе есептеу алгоритмдері жеңіл болатын торлар әдісі қолданылады.
шешімі ізделеді.Мұндай есеп математикалық физика теңдеулер теориясында кеңінен зерттелген. Оның әр түрлі координаттар жүйесіндегі шешімдері және олардың есептеу формулалары да анықталған. Алайда бұл формулалар есептеуге өте қолайсыз. Сондықтан да Дирихле есебін шешу үшін көбінесе есептеу алгоритмдері жеңіл болатын торлар әдісі қолданылады.
(28)-(29) есебін мына айырымдық есебімен жуықтатамыз

 (30)
(30)

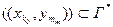 (31)
(31)
(30)- айырымдық теңдеуінің жуықтау дәлдігі төмендегі бағалаудан анықталады
 ,
,


Ал (31) айырымды шекаралық шарттың жуықтау дәлдігі оны қандай әдіспен жуықтатуына байланысты болады. Мәселен, көшіру әдісі қолданылса,онда


Ал енді шекаралық шартты Коллатц әдісін қолданып жуықтатсақ, онда
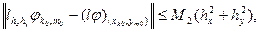
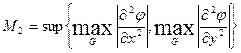
болатыны белгілі.
1.3.2. Айырымдық Дирихле есебінің орнықтылығы
Мүнда (30)-(31) айырымдық есебінің орнықты схема болатынын көрсетеміз. Ол үшін мына теореманы дәлелдейік.
|
|
|
3-Теорема. Егер  облысында анықталған қандай да бір
облысында анықталған қандай да бір  және
және  екі торлық функциялары үшін ішкі тораптарда
екі торлық функциялары үшін ішкі тораптарда
 (
( )-да, (32)
)-да, (32)
ал шекаралық тораптарда
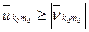 (
( )-да (33)
)-да (33)
теңсіздіктері орындалса, онда 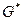 –да
–да
 (34)
(34)
бағалауы орындалады.
Дәлелдеуі. Теореманың шартында берілген (32)-(33) теңсіздіктерін біріктіріп мына түрде жазуға болады
 . (
. ( -да),
-да),
 (
( -да).
-да). 
Демек, 2-теоремаға сәйкес  функциялары
функциялары  –да теріс минимум мәндеріне ие бола алмайды.Алайда,
–да теріс минимум мәндеріне ие бола алмайды.Алайда,  -да:
-да:  және
және  .Ендеше
.Ендеше  -да
-да  және
және  , яғни
, яғни  -да және
-да және  .Демек,
.Демек,  . Теорема дәлелденді.
. Теорема дәлелденді.
Енді (30)-(31) айырымдық есебінің  шешімін
шешімін
 (35)
(35)
түрінде іздейміз. Мұндағы  және
және  функцияларын төмендегі шекаралық есептердің шешімдері ретінде аламыз
функцияларын төмендегі шекаралық есептердің шешімдері ретінде аламыз
 (36)-(37)
(36)-(37)
және
 (38)-(39)
(38)-(39)
Дәлелденген 2 және 3 теоремалары кез-келген және функциялары үшін орындалады. Сондықтан да (6.2.9)-(6.2.10) есебінің шешімі ең үлкен мәнге тек  –да ие болады, яғни
–да ие болады, яғни
 (40)
(40)
Демек,
 (41)
(41)
Енді  функциясының нормасын бағалаймыз. Ол үшін 3-теоремадағыдай
функциясының нормасын бағалаймыз. Ол үшін 3-теоремадағыдай  –ды жоғарыдан шектейтін функцияны құрамыз.
–ды жоғарыдан шектейтін функцияны құрамыз.
Айталық,  тіктөртбұрышы
тіктөртбұрышы  облысын қамтитын ең кіші тіктөртбұрыш болсын (1-сурет). Осы
облысын қамтитын ең кіші тіктөртбұрыш болсын (1-сурет). Осы  –да
–да 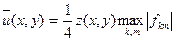 функциясын енгіземіз, мұндағы
функциясын енгіземіз, мұндағы 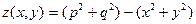 . Енді мына теңдеуді зерттейік:
. Енді мына теңдеуді зерттейік:


Бұл-ортасы  , ал радиусы
, ал радиусы 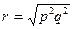 болатын шеңбердің теңдеуі. Егер
болатын шеңбердің теңдеуі. Егер 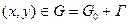 болса, онда
болса, онда  .Сонымен қатар
.Сонымен қатар  болғанда ғана
болғанда ғана  болады. Алайда,
болады. Алайда,  нүктесі
нүктесі  облысында жатпайды. Сондықтан
облысында жатпайды. Сондықтан  , яғни
, яғни 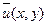 оң мәнді функция. Біз
оң мәнді функция. Біз

болатынын көрсетеміз. Жоғарыда енгізілген  функциясы үшін
функциясы үшін

теңдігі орындалады. Себебі  .
.
Демек, 
Ал 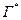 –да (40) шартына сәйкес
–да (40) шартына сәйкес

Сонымен  және
және  торлық функциялары үшін
торлық функциялары үшін

 -да,
-да,

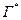 -да
-да
Ендеше 3-теоремасы бойынша

Бұл жәрде нормаға өтсек, онда
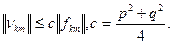 (42)
(42)
бағалауын аламыз. Енді (41) және (42) бағалауларын пайдаланып, (36)теңдігін бағалаймыз

Демек, (30)-(31) айырымдық Дирихле есебі орнықты схема.
1.3.3. Жуық шешімнің жинақтылығы және оның қателігін бағалау
Егер  шекаралық тораптары
шекаралық тораптары  шекарада жатса немесе (28) шекаралық шарты Коллатц әдісі арқылы жуықтатылса, онда (30)-(31) айырымдық есебінің жалпы жуықтау дәлдігі
шекарада жатса немесе (28) шекаралық шарты Коллатц әдісі арқылы жуықтатылса, онда (30)-(31) айырымдық есебінің жалпы жуықтау дәлдігі  шамасында, ал басқа жағдайларда
шамасында, ал басқа жағдайларда  болады. Сонымен қатар (30)-(31) орнықты схема. Демек, Лакс теоремасы бойынша
болады. Сонымен қатар (30)-(31) орнықты схема. Демек, Лакс теоремасы бойынша
|
|
|

шегі орындалады, яғни әрбір  нүктесінде
нүктесінде  жуық шешім
жуық шешім  дәл шешімге жинақталады.
дәл шешімге жинақталады.
Енді осы жинақтылықтың жинақталу жылдамдығын бағалайық. Алдымен (30)-(31) схемасын мына түрде жазайық:
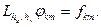
 (43)
(43)
 (44)
(44)
 (45)
(45)
 (46)
(46)
Мұндағы жуықтау  қателігі:
қателігі:


Содан кейін (43)-(44) теңдіктеріне сәйкес (45)-(46) теңдіктерін шегереміз, сонда

немесе
 (47)
(47)
 (48)
(48)
Демек,  қателігі (47)-(48) айырымдық есебінің шешімі. Осы
қателігі (47)-(48) айырымдық есебінің шешімі. Осы  шешімін
шешімін

қосынды түрінде қарастырайық. Мұндағы  және
және  торлық функцияларын
торлық функцияларын
 (49)-(50)
(49)-(50)
және
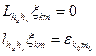 (51)-(52)
(51)-(52)
айырымдық есептерінің шешімдері деп аламыз.
Бірінші пункте дәлелденген 1 және 2 теоремаларына сәйкес (51)-(52) есебінің 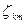 шешімі өзінің ең үлкен мәніне
шешімі өзінің ең үлкен мәніне  шекарада ие болады, яғни
шекарада ие болады, яғни


Ары қарай екінші пунктте баяндалған жолмен 3 теореманы пайдаланып, (49)-(50)есебінің  шешімін былайша бағалаймыз:
шешімін былайша бағалаймыз:

Демек,
 (53)
(53)
Ал егер (29) шекаралық шарты Коллатц әдісі арқылы жуықтатылса, онда
 (54)
(54)
бағалауы орындалады. Мұндағы 
Жоғарыда алынған (53) және (54) бағалаулары есептеу тәжірибесінде сирек қолданылады, өйткені олар  шешімінің туындыларын білуді қажет етеді. Ал ол болса қосымша қиыншылықтар туғызады.
шешімінің туындыларын білуді қажет етеді. Ал ол болса қосымша қиыншылықтар туғызады.
Торлар әдісін қолдану арқылы анықталған  жуық шешім қателігінің реті
жуық шешім қателігінің реті  –ге тең болсын, яғни
–ге тең болсын, яғни

Мұндағы  –қа тәуелсіз тұрақты сан. Сондай-ақ
–қа тәуелсіз тұрақты сан. Сондай-ақ  және
және  айырымды шекаралық есептің тор қадамдары
айырымды шекаралық есептің тор қадамдары  және
және  болған кезде анықталған жуық шешімдері деп қарастырайық.
болған кезде анықталған жуық шешімдері деп қарастырайық.
Онда

деп жазуға болады. Жоруымызға сәйкес
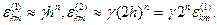
Олай болса
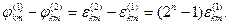
Бұдан

Егер шекаралық шартты Коллатц әдісімен жуықтатсақ, онда  болады. Бұл жағдайда
болады. Бұл жағдайда  жуық шешімінің қателігі
жуық шешімінің қателігі
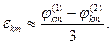
жуық теңдігімен бағаланады. Осы баяндалған әдісті, әдетте Рунге ережесі деп атайды.
|
|
|
1.4. Пуассон теңдеуіне қойылатын Дирхле есебін тіктөртбұрышта шешу
Эллипстік теңдеулерге қойылған шекаралық жүйелерді әр түрлі әдістермен шешуге болады. Егер  шекарасы құрақты тегіс қисықтардан тұратын болса, онда алгебралық жүйенің матрица құрамында қандайда бір заңдылықтың бары байқалмайды. Алайда,
шекарасы құрақты тегіс қисықтардан тұратын болса, онда алгебралық жүйенің матрица құрамында қандайда бір заңдылықтың бары байқалмайды. Алайда,  тіктөртбұрыш немесе квадрат болғанда, матрицаның элементтері белгілі бір тәртіппен орналасады. Мәселен, ол көбінесе үшдиагоналды клеткалы матрица болып келеді. Мұндай жағдайда алгебралық жүйені шешу үшін белгілі қуалау әдісін қолдану қолайлы болатыны белгілі жай. Сондай-ақ бұл жерде итерациялық әдістерді де пайдалану едәуір жеңілдейді.
тіктөртбұрыш немесе квадрат болғанда, матрицаның элементтері белгілі бір тәртіппен орналасады. Мәселен, ол көбінесе үшдиагоналды клеткалы матрица болып келеді. Мұндай жағдайда алгебралық жүйені шешу үшін белгілі қуалау әдісін қолдану қолайлы болатыны белгілі жай. Сондай-ақ бұл жерде итерациялық әдістерді де пайдалану едәуір жеңілдейді.
Айталық, 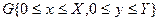 тіктөртбұрышында төмендегі Пуассон теңдеуіне қойылған Дирихле есебі берілсін
тіктөртбұрышында төмендегі Пуассон теңдеуіне қойылған Дирихле есебі берілсін
 (55)
(55)
 (56)
(56)
Сондай-ақ (55)-(56) Дирихле есебінің  шешімі
шешімі  және
және  үзіліссіз дифференциалданатын дербес туындылары бар функция болсын. Осы Дирихле есебін торлар әдісімен шешу мәселесіне тоқталып өтейік.
үзіліссіз дифференциалданатын дербес туындылары бар функция болсын. Осы Дирихле есебін торлар әдісімен шешу мәселесіне тоқталып өтейік.
 тіктөртбұрышында
тіктөртбұрышында

айырымдық торын енгіземіз. Сонда  облысы
облысы  тор облысымен алмастырылады. Мұндағы
тор облысымен алмастырылады. Мұндағы
 ,
,
 -ішкі
-ішкі  тораптар, ал
тораптар, ал 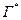 -
-  -шекаралық тораптар жиыны.
-шекаралық тораптар жиыны.
Содан кейін  облысының әрбір торабында (55) Пуассон теңдеуін мынадай айырымдық теңдеумен жуықтатамыз:
облысының әрбір торабында (55) Пуассон теңдеуін мынадай айырымдық теңдеумен жуықтатамыз:
 (57)
(57)


Бұл айырымдық теңдеудің жуықтату дәлдігі-  шамасына тең. Енді
шамасына тең. Енді  айырымдық
айырымдық  тор шекарасы
тор шекарасы  шекарасында жататындай етіп таңдап алынды делік. Сонда (56) шекаралық шарты былайша жуықталады
шекарасында жататындай етіп таңдап алынды делік. Сонда (56) шекаралық шарты былайша жуықталады
 (58)
(58)
яғни  . Демек (56) шекаралық шарттары дәл жуықталады. Ендеше (57)-(58)айырымдық Дирихле есебінің жалпы жуықтау дәлдігі
. Демек (56) шекаралық шарттары дәл жуықталады. Ендеше (57)-(58)айырымдық Дирихле есебінің жалпы жуықтау дәлдігі  шамасында бағаланады. Ал мұндай дәлдікке (57)-(58)есебі
шамасында бағаланады. Ал мұндай дәлдікке (57)-(58)есебі 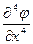 және
және  үзіліссіз дифференциалданатын туындылары бар
үзіліссіз дифференциалданатын туындылары бар  шешімдер жиынында ие болады. Сонымен бірге (57)-(58)-орнықты схема.
шешімдер жиынында ие болады. Сонымен бірге (57)-(58)-орнықты схема.
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 858; Нарушение авторских прав?; Мы поможем в написании вашей работы!