Спектральный анализ периодических сигналов

3.1 Задание для расчёта спектра упрощённым способом

Под упрощённым способом понимается способ вычисления спектра периодических сигналов, основанный на сходстве форм функций спектральной плотности и форм огибающих спектров периодических сигналов. В ходе анализа выполняются следующие задания:

a) используя упомянутое сходство, для периодического сигнала вычислить амплитуды и фазы N значащих гармоник, а также постоянную составляющую;

b) построить диаграммы амплитудного и фазового спектров. Сравнить с диаграммами амплитудной 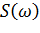и фазовой 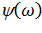характеристик спектральной плотности. Сделать выводы о наблюдениях;

c) выполнить проверку вычислений раздела 2 и подраздела 3.1, получив функцию обратного преобразования Фурье для , построив её диаграмму и сравнив с диаграммой заданного сигнала .

3.2 Задание для расчёта спектра классическим способом – через коэффициенты обобщённого ряда Фурье

Выполняются следующие задания:

a) для того же периодического сигнала напряжения u(t) «в рукопашную» вывести выражения для коэффициентов a₀, a_n и b_n (nÎ [ 1…N ]) обобщенного тригонометрического ряда Фурье

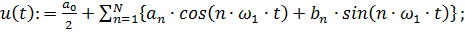
(3.1)

b) используя полученные результаты вычислить те же амплитуды и фазы N значащих гармоник косинусоидального ряда Фурье и постоянной составляющей;

c) построить диаграммы вычисленных амплитудного и фазового спектров. Тип линий диаграмм – «stem». Сравнить с диаграммами спектров 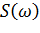и 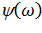, а также диаграммами спектров подраздела 3.1;

d) выполнить проверку вычислений подраздела 3.2, получив функцию обратного преобразования Фурье для , построив её диаграмму и сравнив с диаграммой заданного сигнала

3.3 Рекомендации по анализу спектра периодического сигнала упрощённым способом

a) Для периодически повторяющихся импульсов определяете число гармоник N дискретного спектра с помощью выражения

(3.2)

где циклическая частота первой гармоники

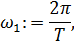
(3.3)

T – период повторения сигнала, заданная для каждого варианта в таблице методички Сильвашко С.А.

b) Вычислить амплитуды и фазы первых N гармоник косинусоидального ряда Фурье и постоянной составляющей

	(3.4)
	(3.5)
	(3.6)

где

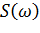c) Построить диаграммы амплитудного , и фазового спектров. Сравнив с диаграммами спектров и 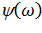, сделать выводы о наблюдениях.

d) Построить временную диаграмму косинусоидального ряда Фурье (от двух до трёх периодов), описываемого выражением

(3.7)

e) Если форма диаграммы качественно отличается от заданного сигнала – проверить вычисления подразделов 2.1 и 3.1.

3.4 Расчёт спектра через коэффициенты обобщённого ряда Фурье

a) Для определения коэффициентов в рукопашную вычислить интегралы

	(3.8)
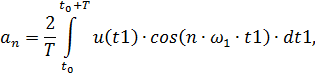
	(3.9)
	(3.10)

где произвольный момент начала интегрирования.

b) Постоянную составляющую, а также амплитуды и фазы первых N гармоник вычисляете с помощью выражений

	(3.11)
	(3.12)
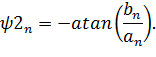
	(3.13)

c) Построить диаграммы амплитудного и фазового спектров. Тип линии диаграмм – «stem». Сравнить с диаграммами спектров 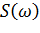и 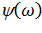, а также с диаграммами и 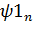. Если амплитудный спектр 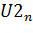отличается от – проверить вычисления пунктов a) и b) настоящего подраздела 3.4.

d) Построить временную диаграмму косинусоидального ряда Фурье

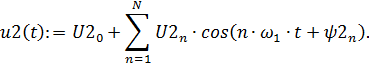
(3.14)

e) Если форма диаграммы качественно отличается от заданного сигнала – проверить вычисления пунктов a) – d) настоящего подраздела 3.4.

4 Расчёт операторной передаточной функции и частотных характеристик избирательной цепи

4.1 Задание на расчёт

На данном этапе выполняются следующие задачи:

a) заменить в заданной избирательной цепи реактивные элементы их операторными сопротивлениями. Любым удобным методом расчёта получить выражение для операторной передаточной функции 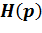. Упростить выражение до правильной двухэтажной дроби;

b) выполнив в полученной функции 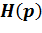замену p=j·ω, получить функцию комплексной частотной характеристики ;

c) на основе выражения в рукопашную вывести выражения для амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристик и ;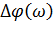

d) построить диаграммы вычисленных АЧХ и ФЧХ. Сравнив диаграммы АЧХ и любого из амплитудных спектров входного сигнала u(t) либо u_p(t), сделать качественное заключение о степени искажения выходного сигнала.

4.2 Рекомендации к расчёту операторной передаточной функции

Расчёт передаточной функции

(4.1)

где изображения по Лапласу входного и выходного напряжения соответственно – покажем на примере схемы рисунка Рисунок 4.1,а. Предварительно заменяем реактивные элементы (рисунок Рисунок 4.1,б):

- индуктивности L – операторным сопротивлением Z=p·L;

- конденсаторы C – сопротивлением .

а)

б)

Рисунок 4.1

После этого получить операторную передаточную функцию (4.1) возможно всеми известными вам методами расчёта линейных резистивных цепей постоянного тока. В данной методичке попробуем решить поставленную задачу двумя методами:

- методом пропорциональных величин;

- методом узловых потенциалов.

Вообще же вы может применить и любые другие методы.

4.2.1 Расчёт методом пропорциональных величин

a) Задаём на самом удалённом от входа участке цепи – на выходе – значение напряжения

U2=1.

(4.2)

Последовательно двигаясь от выхода к входу будем вычислять токи и напряжения, пока не определим выражение для U1.

b) Следующие величины, которые можем определить в одно действие (рисунок 4.1,б) – токи нагрузки, катушки L1 и ёмкости C1:

	(4.3)
	(4.4)
	(4.5)

c) Следующая величина – ток катушки L2, который определим по первому закону Кирхгоффа

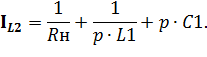
(4.6)

При получении передаточной функции (4.1) имеет смысл результаты промежуточных преобразований также доводить до правильной рациональной дроби (чисто по техническим причинам). Для выполнения таких преобразований, в целях избавления от рутинных вычислений, можете воспользоваться символьными вычислениями программами MathCad. Например, упрощение выражения (4.6) можете следующим образом:

- вводите в MathCad выражение (4.6) (рисунок Рисунок 4.2,а);

- выделяете в нём упрощаемую часть – всё выражение справа от знака «=» (рисунок Рисунок 4.2,б);

- активируете в главном меню команду «S ymbolics», затем команду «F actor» (рисунок Рисунок 4.2,в). В результате получите правильную рациональную дробь (рисунок Рисунок 4.2,г)

(4.7)

d) Следующая электрическая величина – суммарное падение напряжения на катушке L2 и резисторе Rн, которое определим по закону Ома

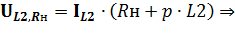
	(4.8)
	(4.9)

а)	г)
б)
с)

Рисунок 4.2

e) Следующая электрическая величина (и последняя) – входное напряжение U1, которое определим по второму закону Кирхгоффа

	(4.10)

В программе MathCad из суммы (4.10) можем получить выражение функции U1(p) следующим образом:

- набираем в программе выражения (4.9) и (4.10), выделяем правую часть выражения (4.9) (рисунок Рисунок 4.3,а) и копируем её в буфер памяти (команда «Copy» контекстного меню);

- выделяем переменную «U _{L 2, R н}» выражения (4.10) (рисунок 4.3,б);

а)	б)
в)

Рисунок 4.3

- затем выполняем команду «S ymbolics»→«V ariable» →«S u bstitute» (рисунок Рисунок 4.3,б). В результате получим дробно-рациональное выражение (рисунок Рисунок 4.3,в)

(4.11)

f) В программе MathCad выражение передаточной функции можете получить следующим образом:

- набираете в программе выражение

,

(4.12)

при этом дробь вводить не обязательно;

- подставляем в числитель последней дроби (4.12) «единицу», а на место знаменателя копируем выражение (4.11) (рисунок Рисунок 4.4,а);

- выделив полученную дробь и используя команду «S ymbolics»→«F actor» или «S ymbolics»→«S implify», получаем дробно-рациональное выражение передаточной функции (рисунок Рисунок 4.4,б)

	(4.13)
	а)
	б)

Рисунок 4.4

Выражение (4.13) можно ввести в MathCad и не прибегая к символьным вычислениям. Выполняете это следующим образом:

- набираете в программе MathCad заготовку для H(p) (рисунок Рисунок 4.5,а);

- на место знаменателя копируете числитель дроби (4.11), на место числителя – знаменатель дроби (4.11) (рисунок Рисунок 4.5,б).

а)

б)

Рисунок 4.5

4.2.2 Расчёт передаточной функции методом узловых потенциалов

a) Задаём единичное напряжение на входе (рисунок Рисунок 4.6)

U1=1.

(4.14)

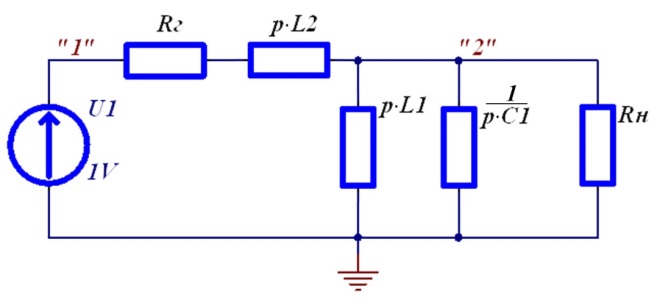
Рисунок 4.6

b) Анализируемая схема содержит всего два узла, потенциал одного из которых нулевой. Поэтому метод узловых потенциалов упрощается до метода двух узлов, а для определения U2 составляется одно уравнение для узла «2»

(4.15)

где 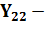собственная проводимость узла «2»

(4.16)

c) Из уравнения (4.15) и выражения (4.16) получим U2

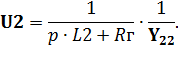
(4.17)

d) Функцию U2(p) получим, выполнив следующее:

- выражение (4.16) и (4.17) вводим в MathCad (рисунок Рисунок 4.7,а);

- выделяем правую часть (4.16) и сбрасываем в буфер памяти (рисунок Рисунок 4.7,а);

- выделяем переменную Y₂₂ в выражении (4.17) (рисунок Рисунок 4.7,б);

а)

б)

Рисунок 4.7

- используя команду «S ymbolics»→«V ariable» →«S u bstitute» (рисунок Рисунок 4.7,б), получаем выражение для U2 как функцию частоты p (рисунок Рисунок 4.8)

(4.18)

e) Так как U1 =1, то функция коэффициента передачи примет такое же выражение, что и (4.16)

(4.19)

 

Рисунок 4.8

Дата добавления: 2017-01-14