Список источников

Выводы и рекомендации

МКЭ модель

Геометрическая модель рамы

Допущения

Физические допущения:

o Крепление стержней абсолютно жёсткие;

o Используется критерий «Хубера-Мизеса»; для определения эквивалентных напряжений

o Весовая нагрузка, приложенная к пластине опоры равномерно разносится на четыре её угла;

Моделирование стержней балки проводится в программе ANSYS с помощью элементов BEAM 188 учитывающих изгиб и сдвиг в двух направлениях, а так же угловые деформации скручивания. Система координат конечного элемента BEAM 188, в которой программа предоставляет результаты расчёта, представлена на рисунке Рисунок 8.

 

Рисунок 8. Система координат балочного элемента

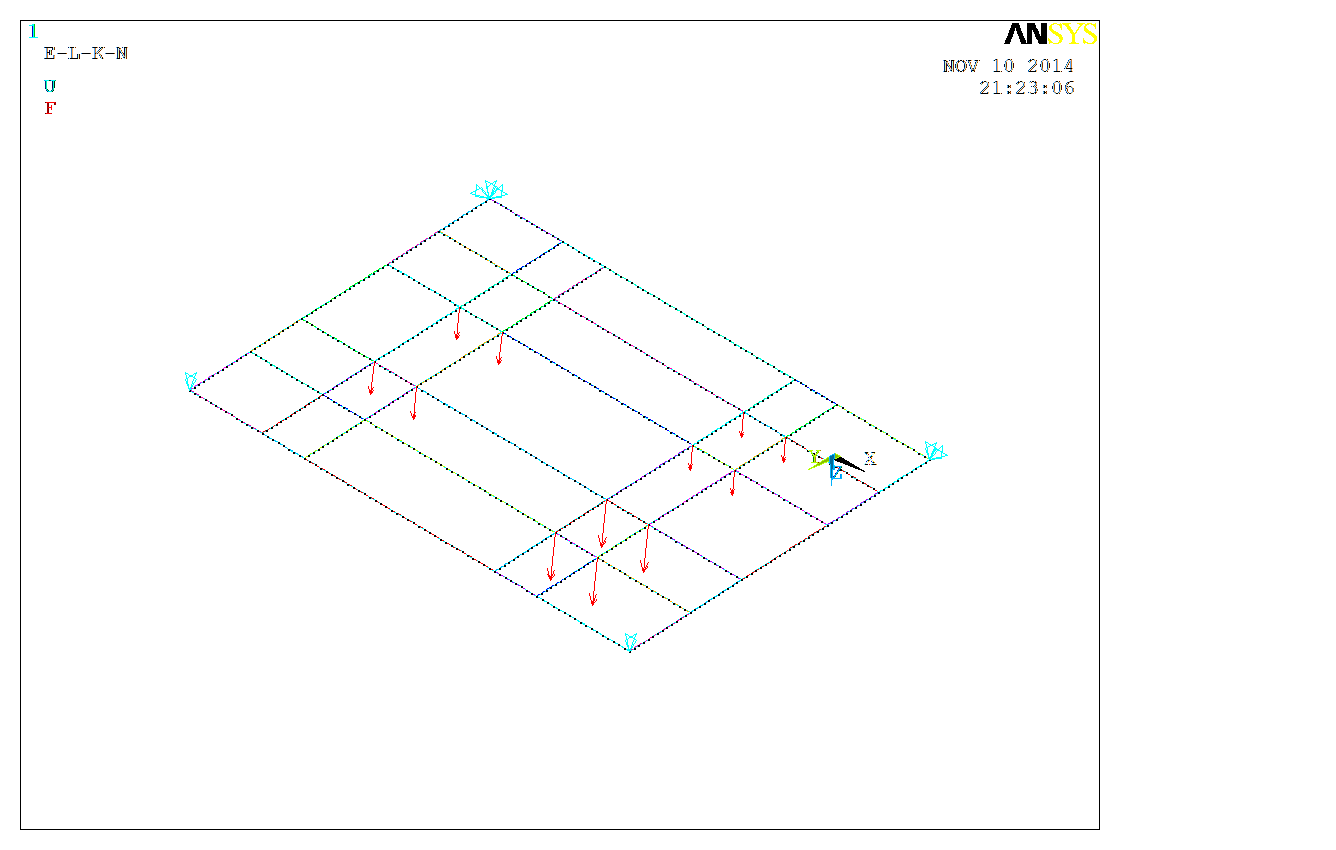
Схематичное изображение рамы показано на рисунке Рисунок 9. На рисунке показана нагрузка, приведённая к точкам рамы и внешние закрепления.

 

Рисунок 9. Геометрическая модель рамы

Вид рамы после разбивки на конечные элементы приведён на рисунке Рисунок 10.

 

Рисунок 10. Конечно-элементная модель рамы

6 Расчёт прочности и жёсткости рамы

Рама является плоско-пространственной. Поэтому существенными силовыми факторами в ней будут изгибающий, относительно оси Y (Рисунок 8) момент M_y и крутящий момент M_k. Некоторые стержни рамы являются короткими и,строго говоря, они должны рассчитываться на сдвиг под действием поперечной силы, однако для используемого профиля достаточно сложно определить коэффициенты пропорциональности Q_z и τ_xz. Поэтому в расчёте учитывается только изгибающий и крутящий моменты.

6.1 Нагружение «А»

6.1.1 Картина прогибов при нагружении «А»

Картина перемещений представлена ниже (Рисунок 11).

Рисунок 11. Прогибы балок рамы u, мм. Максимальное перемещение u_max =1,85 мм.

6.1.2 Эпюры моментов при нагружении «А»

Ниже приведены эпюры изгибающего M_Y (Рисунок 12) и крутящего M_K (Рисунок 13) моментов.

Рисунок 12. Изгибающий момент M_Y, Н·мм, максимальное значение M_Y,=985 Н·м

Рисунок 13. Крутящий момент M_K, Н·мм максимальное значение M_K =106 Нм M_K,=10 600 Н·мм

6.1.3 Эпюра эквивалентных напряжений при нагружении «А»

Для упрощения расчётов предполагается, что в пределах каждого сечения максимальное напряжение от изгиба и кручения достигаются в одной точке. Данное допущение идёт в запас. Тогда эквивалентное напряжение можно вычислить на основании критерия Хубера-Мизиса можно вычислить по формуле:

(8)

Распределение эквивалентных напряжений, вычисленных по формуле (8) представлено на рисунке Рисунок 14.

 

Рисунок 14. Эпюра эквивалентных напряжений σe, МПа максимальное значение σe=14,1 МПа

6.2 Нагружение «Б»

6.2.1 Картина прогибов при нагружении «Б»

Картина перемещений представлена ниже (Рисунок 15).

Рисунок 15. Прогибы балок рамы u, мм. Максимальное перемещение u_max =1,81 мм.

6.2.2 Эпюры моментов при нагружении «Б»

Ниже приведены эпюры изгибающего M_Y (Рисунок 16) и крутящего M_K (Рисунок 17) моментов.

Рисунок 16. Изгибающий момент M_Y, Н·мм, максимальное значение M_Y,=861 Н·м

Рисунок 17. Крутящий момент M_K, Н·мм, максимальное значение M_K =90 Н·м

6.2.3 Эпюра эквивалентных напряжений при нагружении «Б»

Распределение эквивалентных напряжений, вычисленных по формуле (8) представлено на рисунке Рисунок 18.

Рисунок 18. Эпюра эквивалентных напряжений σ_e, МПа максимальное значение σ_e,=12,2 МПа,

а) Численные результаты расчёта представлены в таблице Таблица 1.

Таблица 1. Результаты расчёта

	А	Б
Максимальное перемещение umax, мм	1,85	1,81
Максимальное эквивалентное напряжение σe, мм	14,1	12,2
Коэффициент запаса по текучести, nT

б) Рама преимущественно работает на изгиб: изгибающие момент на порядок больше крутящего. Необходимо обеспечить с помощью креплений достаточно жёсткую передачу изгибающего момента.

в) В расчёте не учтены действия локальных концентраций напряжений и действия поперечных, сдвигающих сил, массы самих стержней и нагрузки на раму от веса дополнительного оборудования и персонала. Поэтому полученные достаточно большие значения коэффициенты запаса можно считать приемлемыми.

г) Смещения кареток слабо влияет на напряжения и деформации, поскольку их вес мал по сравнению со станиной. Наиболее опасное состояние, по-видимому, когда центр масс конструкции ближе всего к центру рамы. Смещение нагрузки к краям или добавление нагрузки на краю (например, от массы персонала) не значительно будет влиять на напряжённо-деформированное состояние.

1. Онлайн ресурс компании Kanya AG, Switzerland. Режим доступа: http://www.kanya.com/global/PVS-pdf/2003_PVS_engl.pdf (посещено 04.11.2014).

2. Онлайн ресурс по алюминиевым сплавам. Режим доступа: http://aluminium-guide.ru/alyuminievyj-splav-6063/ (посещено 04.11.2014).

3. Тимошенко С.П., Гудьер Дж. Теория упругости: Пер. с англ. / Под ред. Г.С. Шапиро. - 2-у изд. - М. Наука. Главная редакция физико-математической литературы, 1979, 560 с.

4.

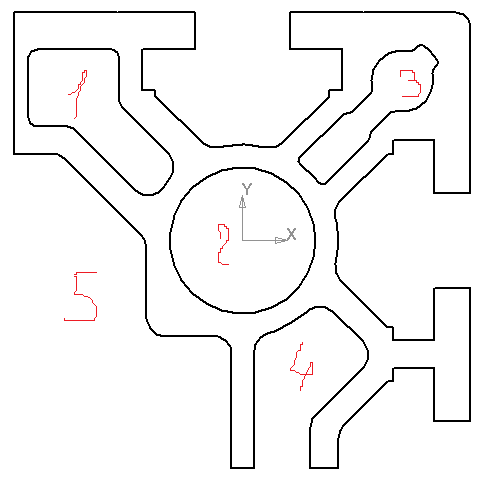
П.1 Приложение для расчёта параметров сечения

Рисунок 19. Нумерация контуров

clc

clear all

% Удельные потоки графиента fi в контура

% Расчет с f

Vq=[-96.25428 -84.23069 -83.3975 -67.25341 -84.1073]';

% Расчет с первой областью

v1=[15.82613 -2.29743 -4.89035e-6 -3.03897e-8 -5.59279]';

v2=[-2.28783 20.01418 -2.05117 -3.52686 -5.14484]';

v3=[-4.86584e-6 -2.04802 17.33637 -5.63115e-6 -3.69378e-9]';

v4=[-3.01897e-8 -3.52797 -5.65846e-6 17.13007 -5.74495]';

v5=[-5.59244 -5.14286 -3.68199e-9 -5.733 16.48284]';

% Площади внутренних контуров - Определены графически

A=[134.582925;

201.061930;

80.245194;

145.553706;

589.263411];

% M=[v1 v2 v3 v4 v5]'*q+Vq=[A]

M=[v1 v2 v3 v4 v5]';

% Значения функции напряжений на внутренних контурах

Fi_i=M^-1*[2*A-Vq]

MM=(sum(q.*A)+43217.11654)*4*2

tau=87.06949

tauM=50

Wk=MM/tau

% если исключить самую опасную точку

WkM=MM/tauM

J=MM*2

П.2 Приложение MATLAB для разноса опорных реакций

clc

clear all

close all

X=[250 -174 -366 -1236 -1428 -1760];

Z=[-212 55 325 775 1045 1362];

m=1640;

Xc=[-598 -630];

Zc=[576 553];

Zo=mean(Z([2 3 4

3 4 5]));

Xo=mean(X([2 2 4

3 3 5]));

M=[1 1 1

Xo

Zo];

v=[1 1;Xc;Zc]*m;

Fo=M^-1*v;

disp('Реакции в опорах')

str2num(num2str(Fo',4))

Дата добавления: 2017-01-14