Дифракция Фрайнгофера на одной щели. Дафракционная решетка

Дифракция в параллельных лучах или дифракция
И. Фраунгофера (1787-1826 г.) наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Рассмотрим дифракцию Фраунгофера от бесконечно длинной щели. Пусть плоская монохроматическая волна падает нормально плоскости узкой щели шириной (рис.17. 2). Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении равна: ,(17.9);где – основание перпендикуляра, опущенного из т. М на луч ND. Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна , т.е. всего на величине щели уместится зон. Плоскость щели совпадает с волновым фронтом, т.к. свет падает на щель нормально; вследствие этого все точки волнового фронта будут колебаться в одинаковой фазе. Амплитуды вторичных волн в плоскости щели будут равны. 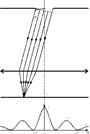Рис. 17.2. Из выражения (17.9) следует, что число зон Френеля, укладывающихся на ширине щели, зависит от угла . При интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, т.к. колебания от каждой пары соседних зон взаимно гасят друг друга. Т.е. если число зон Френеля четное, то:

,(17.10)и в т. В наблюдается дифракционный минимум (полная темнота). Если число зон Френеля нечетное,то: 17.11, и наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля. В направлении 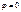щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью, т.е. в т. 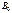наблюдается центральный дифракционный максимум. Из условий (17.10) и (17.11) можно найти направления на точки экрана, в которых амплитуда, а следовательно и интенсивность, равна нулю(17.12):

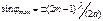.Распределение интенсивности на экране, получаемое вследствие дифракции (дифракционный спектр), приведено на рис. 17.2.Расчеты показывают, что интенсивности в центральном и последующем максимумах относятся как: 0,047:0,017:0,0083:..., т.е. основная часть световой энергии сосредоточена в центральном максимуме. Сужение щели приводит к тому, что центральный максимум расплывается, а интенсивность уменьшается.

Дифракционная решетка представляет собой систему параллельных щелейравной ширины а, лежащих в одной плоскости и разделенный равными по ширине промежутками б. наблюдаемая в дифракционной решетке картина определяется как результат взаимной интерференции идущих от всех щелей волн, что приводит к появлению кроме основных дифракционных максимумов и минимумов дополнительные минимумы. Для дифракционной решетки, имеющий N щелей, между двумя главными максимумами распологается N-1 дополнительных минимума, разделенных вторичными максимумами. Условием главных максимумов(17.13): 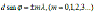, а условием дополнительн. минимумов (17.13):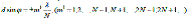

Где 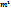может принамать значения, кроме: 0, N, 2N…

65. Поляризация света. Закон Малюса. Из теории Максвелла следует, что электромагнитные волны, включая световые, являются поперечными: век-торы напряженностей эл. и магн. полей волны взаим-но перпендикулярны и колеблются перпендикулярно век-тору скорости распространения волны. Обычно при описа-нии электромагн. волн используют вектор напряженности эл.поля.Свет представляет собой суммарное электро-магн. излучение множества атомов. Свет со всевозмож-ными равновероятными ориентациями вектора (а, сле-довательно, и ), называется естественным (рис.18. 1а). 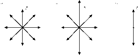Рис.18.1.С вет, в котором направления колебаний светового вектора упорядочены, называется поляризованным. Если в результате внешних воздействий появляется преимущест-венное, но не исключительное, направление колебаний , то имеют дело с частично поляризованным светом (рис.18.1б). Свет, в котором вектор колеблется только в одном направлении, перпендикулярном лучу, называется плоскополяризованным (линейно поляризованным, рис 1в). Плоскость, проходящая через направление колебаний светового вектора поляризованной волны и направление распространения этой волны, называется плоскостью поляризации. Эллиптически поляризованный свет – свет, для которого вектор 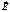(вектор ) изменяется со временем так, что его конец описывает эллипс, лежащий в плоскости, перпендикулярной лучу. Если эллипс поляризации вырождается в прямую, (при разности фаз, равной 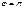или 0), то имеем дело с плоскополяризованным светом, если в окружность (при разности фаз, равной 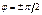и равенстве амплитуд складываемых сигналов), то имеем дело с циркулярно поляризованным (поляризованным по кругу) светом. Степенью поляризации называется величина: (18.1); и 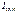, соответственно, макс. и мин. интенсивность частично поляризованного све-та, пропускаемого анализатором. Для естественного света: и 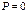. Для плоскополяризованного света: 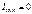и . Естественный свет можно преобразовать в плоскополяризованный, применяя поляризаторы. В качестве поляризатора могут быть использованы анизотропные среды, например, кристаллы турмалина. Пусть естественный свет падает перпендикулярно пластинке турмалина Т1, вырезанной параллельно оптической оси ОО’(рис.18.2). При вращении кристалла Т1 вокруг направления луча изменений интенсивности прошедшего через пластинку света не наблюдается. 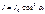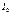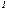Если на пути луча разместить вторую пластинку Т2, и вращать ее вокруг направления луча, то интенсивность света, прошедшего через пластинку, меняется в зависимости от угла между оптическими осями кристаллов по закону Малюса: ,(18.2); и - соответственно, интенсивности света, попадающего на второй кристалл, и вышедшего из него. 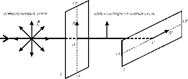Рис. 18.2. Интенсивность прошедшего через пластинку света изменяется от минимума (при ) до максимума (при 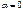) (оптические оси пластинок параллельны). Пластинка Т1, преобразующая естественный свет в плоскополяризованный, является поляризатором. Пластинка Т2, служащая для анализа степени поляризации света, называется анализатором. Обе пластинки совершенно одинаковы. Если естественный свет пропустить через 2 поляризатора, главные плоскости которых образуют угол 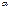, то из первого выйдет плоскополяризованный свет, интенсивность которого 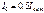, из второго, согласно выражению (18.2), выйдет свет интенсивностью 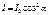. Интенсивность света, прошедшего два поляризатора, определяется: 18.3;откуда: 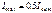(поляризаторы параллельны) и 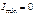(поляризаторы скрещены).

Дата добавления: 2017-01-14