Вариньон теоремасы. 2 страница

37. Қатты дененің жазық параллель қозғалысы, оның кинематикалық сипаттамалары

Егер дененің барлық нүктелері қозғалмайтын жазықтыққа параллель көшіп отырса, онда дененің қозғалысын жазық-параллель қозғалыс деп атаймыз. Жазық-параллель қозғалыста денедегі 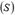қима қозғалмайтын жазықтыққа параллель қозғалып отырады. Дененің қозғалысын анықтау үшін қиманың қозғалысын білген жеткілікті. қиманың әр сәттегі өз жазықтығындағы орны оның кез келген А,В нүктелерімен немесе AB кесіндісімен анықталады. Негізгі кинематикалық сипаттамалар: V -жылдамдық, a -үдеу, -бұрыштың жылдамдық, -бұрыштық үдеу болады. Олар дене қозғалысының теңдеулерінен табылады.

38. Жылдамдықтардың лездік центрі және оның орнын анықтаудың дербес жағдайлары.

Дененің қимасының қозғалысында кез келген уақытта жылдамдығы нөлге тең бір нүкте болады. Ол нүктені айналу центрі немесе жылдамдықтардың лездік центрі деп атаймыз. Лездік жылдамдықтар центрін табудың дербес жағдайларын келтірейік:

а) Егер жазық-паралель қозғалыста бір цилиндрлік дене екінші қозғалмайтын цилиндрлік дененің бетімен сырғанамай қозғалатын болса, олардың жанасу нүктесі лездік жылдамдықтар центрі болады.

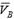б) Егер А, В нүктелерінің жылдамдықтары өзара параллель және болса, онда лездік жылдамдықтар центрі АВ сызық пен және жылдамдықтардың ұштарынан өтетін түзудің қиылысында жатады.

в) Егер болып, болмаса, онда А, В нүктерінде құрылған перпендикулярлар өзара қиылыспайды, лездік жылдамдықтар центрі мүндай жағдайда болмайды.Теорема бойынша , яғни . Демек, мұндай жағдайда қарастырылып жатқан сәтте барлық нүктелердің жылдамдықтары өзара тең болады. Онда дененің қозғалысы лездік ілгерілемелі қозғалыс болады және

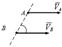
г.

39. Жылдамдықтардың лездік центрі жіне оның көмегімен жазық қима нүктелерінің жылдамдықтарын анықтау

Дененің (S) қимасының қозғалысында кез келген уақытта жылдамдығы нөлге тең бір нүкте болады. Ол нүктені айналу центрі немесе жылдамдықтардың лездік центрі деп атаймыз. Ондай нүкте кез келген уақытта бар болады және жалғыз. Оны Р деп белгілейік. Енді P нүктені полюс деп алсақ Демек, (S) қиманың кез келген нүктесінің жылдамдығы оның P нүктені айнала қозғалудағы жылдамдығына тең: Онда .

Яғни, дене нүктелерінің жылдамдықтары олардың лездік жылдамдықтар центріне дейінгі қашықтықтарына пропорционал болады. Сонымен,

1) Кез келген нүктенің жылдамдығын табу үшін бір нүктенің жылдамдығы (модулі, бағыты) және ізделінді жылдамдықтың бағыты белгілі болуы керек.

2) Лездік жылдамдықтар центрін табу үшін екі нүктенің жылдамдықтарына сол нүктелерде перпендикулярлар құру қажет. Олардың қиылысу нүктесі лездік жылдамдықтар центрін береді.

40. Нүктенің абсолют, салыстырмалы жіне тасымал жылдамдығы. Күрделі қозғалыстағы нүктенің жылдамдықтарын қосу туралы теорема.

. Егер нүкте екі немесе одан артық қарапайым қозғалыстарға қатысса, онда нүктенің қозғалысын күрделі қозғалыс деп атаймыз.

Дененің МD нүктесінің қозғалысын М нүкте үшін тасымал қозғалыс деп атаймыз. М нүктенің D денеге немесе Oxyz жүйеге қатысты өз қозғалысын оның салыстырмалы қозғалысы дейміз. М нүктенің абсолют қозғалысы - радиус вектормен, “О” полюстің абсолют қозғалысы 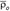- радиус вектормен, М нүктенің салыстырмалы қозғалысының 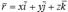радиус векторымен беріледі.

Жалпы жағдайда, МD нүкте “О” полюспен бірге ілгерілемелі және полюсқа қатысты айналма қозғалыста болады. Нүктенің абсолют қозғалысы теңдеуімен беріледі. Олай болса абсолют жылдамдық 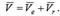Теорема. Нүктенің абсолют жылдамдығы оның тасымал және салыстырмалы қозғалыс жылдамдықтарының геометриялық қосындысына тең. Абсолют жылдамдықтың сан мәні (модулі)

41. Күрделі қозғалыстағы нүктенің үдеулерін қосу туралы теорема.

Нүктенің абсолют үдеуін табу үшін абсолют жылдамдықтан уақыт бойынша туынды аламыз. Сонда мұндағы - Кориолис немесе бұру үдеуі деп аталады, яғни нүктенің Теорема. Нүктенің абсолют үдеуі оның тасымал, салыстырмалы және Кориолис үлеулерінің геометриялық қосындысына тең. Абсолют үдеудің сан мәні (модулі) Теорема. Егер тасымал қозғалыс ілгерілемелі болса, онда абсолют үдеу тасымал және салыстырмалы үдеулердің геометриялық қосындысына тең. Бұл жағдайда абсолют үдеудің модулі

42. Кариолис үдеуінің абсолют шамасы мен бағыты.

Нүктенің Кориолис үдеуі тасымал қозғалыстың бұрыштық жылдамдығы мен салыстырмалы жылдамдықтың екі еселенген векторлық көбейтіндісіне тең. Кориолис удеуі векторының бағыты және векторлары арқылы өтетін жазықтыққа перпендикуляр. Жуковский ережесі: Кориолис удеуі векторының бағытын анықтау үшін салыстырмалы жылдамдық векторын тасымал бұрыштық жылдамдық векторына перпендикуляр жазықтыққа проекциялап, осы проекцияны дененің айналу бағытында -қа бұру қажет. Кориолис үдеуінің модулі

43. Динамиканың заңдары.

Динамика – күш әсерінен материялық

денелердің қозғалысын зерттейтін теориялық механиканың бөлімі. Динамикада тек тұрақты күштер ғана емес, сонымен бірге уақытқа, координаталарға және жылдамдыққа тәуелді айнымалы күштер де қарастырылады. Айнымалы күштер тұрақты күштердің заңдарына бағынады,яғни оларды қосуға, жіктеуге болады, олардың моменттері және т.б. болады. Ньютонның үш заңы материялық нүкте динамикасының негізгі заңдары болып табылады.Ньютонның бірінші заңы. Егер материялық нүктеге сырттан ешбір күш әсер етпесе немесе әсер ететін күштер жүйесі нөлге пара-пар болса, онда нүкте тыныштық күйде немесе бірқалыпты және түзу сызықты қозғалыста болады. Ньютонның бірінші заңы орындалатын санақ жүйелері инерциялық санақ жүйелері деп аталады.Ньютонның екінші заңы (динамиканың негізгі заңы). Материялықнүктенің үдеуі оған әсер етуші күшке тура пропорционал, бағыты күшпенбағыттас. Нүкте массасы пропорционалдық коэффициент болып табылады.Бұл заңның математикалық өрнегі:

Ньютонның үшінші заңы. Екі материялық нүкте бір-біріне модульдері

тең, бір түзудің бойымен қарама-қарсы бағытталған күштермен әсер етеді.

44. Материалық нүкте динамикасының екі негізгі мәселесі жіне олардың шешуі

Материялық нүктенің негізгі мәселелері еркін және еркін емес нүктелер үшін айтылады.Қозғалысы басқа денелермен шектелмеген нүктені еркін материялық нүкте дейміз. Осындай нүкте үшін динамиканың екі негізгі мәселесі қарастырылады: Динамиканың бірінші негізгі мәселесі: Нүктенің массасын, қозғалыс заңын және оған әсер ететін актив күштерді біле отырып, реакция күштерінанықтау.Динамиканың екінші негізгі мәселесі: Нүктенің массасын және оған әсер ететін актив күштерді біле отырып, оның қозғалыс заңын және реакция күштерін анықтау. Екі мәселе де Ньютонның екінші заңының көмегімен шешіледі.Қозғалысы басқа денелермен шектелген нүкте еркін емес материялықнүкте деп аталады.

өрнегімен еркін емес нүкте үшін де динамиканың екі негізгі мәселесі шешіледі: Бұл мәселені шешу үшін Ньютонның екінші заңын құрып, сосын оны координата өстеріне проекциялаукерек. Нүкте динамикасының екінші мәселесінің шешуі белгісіз x, y, z

функцияларына қатысты екінші дәрежелі үш дифференциалдық теңдеулержүйесінен тұратын оның қозғалысының дифференциалдық теңдеулерін интегралдауға тіреледі.Бұл теңдеулердің жалпы шешімі С1, С2, …, С6 алты интегралдық тұрақтыларға тәуелді:

45. Нүктенің кинетикалық энергиясы және оның өзгеруі туралы теорема

Нүктенің кинетикалық энергиясы деп оның массасы мен

жылдамдығының квадратының көбейтіндісінің жартысына тең mV2/2 скаляр шаманы айтады. Нүкте динамикасының негізгі теңдеуінен (Ньютонның екінші заңы):

бұл нүктенің кинетикалық энергиясының өзгеруі туралы теореманыңдифференциалдық түрі деп аталады: нүктенің кинетикалық энергиясыныңтолық дифференциалы нүктеге әсер ететін барлық күштердің элементар жұмыстарының қосындысына тең.Бұл теоремадан

екенін көреміз, яғни нүктенің кинетикалық энергиясының толық дифференциалы нүктеге әсер ететін барлық күштердің қуаттарыныңқосындысына тең.

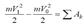нүктенің кинетикалық энергиясының өзгеруі туралы теореманың интегралдық(шекті)түрін береді: нүкте шекті орын ауыстырғандағы оныңкинетикалық энергиясының өзгеруі осы орын ауыстыруда нүктеге әсер ететін барлық күштердің жұмыстарының алгебралық қосындысына тең.

46. Нүктенің қозғалыс мөлшерінің өзгеруі туралы теорема. Нүкте үдеуінің векторы жылдамдық векторынан уақыт бойынша алынған бірінші туындыға тең 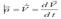екенін ескерсек,нүкте динамикасының негізгі заңын

былай жазуға болады: теңдеуі нүктенің қозғалыс мөлшерінің өзгеруі туралы теореманыңдифференциалдық түрін береді: нүктенің қозғалыс мөлшерінің уақытбойынша бірінші туындысы нүктеге әсер ететін барлық күштердің геометриялық қосындысына тең.

теңдеуі нүктенің қозғалыс мөлшерінің өзгеруі туралытеореманың интералдық (шекті) түрін береді: шекті уақыт аралығындағы нүктенің қозғалыс мөлшерінің өзгеруі осы уақыт аралығында нүктеге әсер ететін барлық күштер импульстерінің геометриялық қосындысына тең.

47. Күш жұмысы.Ауырлық, серпімділік, үйкеліс күштерінің жұмысы.

Нүкте орын ауыстырғандағы күш әсерінсипаттау үшін жұмыс ұғымы қолданылады. М нүктесіне әсер ететін Fкүшініңэлементар жұмысыдеп

(1) скаляр шамасын айтады, мұндағы F ז - Fкүшінің М ז жанамаөске проекциясы (немесе Fкүшінің Мнүктесінің Vжылдамдығы бағытынапроекциясы); ds – М нүктесінің элементар орын ауыстыру модулі.

Ауырлық күші mg әсер ететін нүкте бастапқы М0 (x0, y0, z0) орнынан М1 (x1, y1,z1)-ге орын ауыстырсын. Ауырлық күшінің жұмысын (1) өрнегімен есептейік,сонда A(mg)=+-mg, h=z0 -z1- нүктенің орын ауыстыру биіктігі. Демек, ауырлық күшінің жұмысы плюс не минус таңбасымен алынған ауырлық күші модулі мен вертикаль орын ауыстырудың көбейтіндісіне теңекен. Плюс таңбасы нүкте төмен орын ауыстырғанда, ал минус таңбасы нүкте жоғары қарай орын ауыстырғанда алынады.

Серпімділік күшінің жұмысы. Серіппенің бос ұшына бекітілген және горизонталь жазықтықта жатқан М жүгін қарастырайық.Координатаның О бас нүктесі етіп созылмаған серіппенің ұшын аламыз(l0 –деформацияланбаған серіппенің ұзындығы). Егер жүкті О тепе-теңдік орнынан серіппенің ұзындығы lболатындай етіп созсақ, серіппе -ге созылады да, жүкке Онүктесіне бағытталған серпімділік күші Fсерп әсер етеді. 25-суреттен λ=x екенін көреміз, сондықтан серпімділік күшін былай жазуға болады: 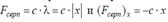мұндағы с – серіппенің серпімділік коэффициенті.

Демек, серпімділік күшінің жұмысы серіппенің серпімділік коэффициенті мен бастапқы және соңғы деформациялар квадраттары айырмасының көбейтіндісінің жартысына тең.(21) өрнегі М нүктесінің орын ауыстыруы түзу сызықты болмаса да орын алады. Бұл серпімділік күшінің жұмысы нүктетраекториясының түрінетәуелді емес екендігін көрсетеді.Үйкеліс күшінің жұмысы. Егер нүкте кедір-бұдырлы жазықтықпен қозғалса, оған әсер ететін үйкеліс күшінің модулі f N болады. Бұл жерде f –үйкеліс коэффициенті, ал N – жазықтықтың нормаль реакциясы. Үйкеліс күші қозғалысқа қарсы бағытталғандықтан Сонымен, сырғанау үйкелісі күшінің жұмысы әрқашан теріс таңбалы және нүктенің жүріп өткен жолына тәуелді екен.

48. Материялық нүкте үшін Даламбер принципі. Материялық нүкте үшін Даламбер принципі нүкте динамикасының есептерін статиканың

қарапайым әдістерімен шығаруға мүмкіндік береді. материялық нүкте үшін Даламбер принципі деп аталады:қозғалыстағы материялық нүктеге әсер ететін актив күштер, реакция күші мен инерция күші теңестірілген күштер жүйесін құрайды. Бірақ материялық нүктеге тек актив күштер мен реакция күші ғана әсер ететін ескеру керек, ал

инерция күші нүктеге әсер етпейді, сондықтан да ол жасанды күш болады.

49. Нүктенің қозғалыс мөлшері және күш импульсі

Нүкте қозғалысының негізгі динамикалық сипаттамаларының бірі – қозғалыс мөлшері.Нүктенің қозғалыс мөлшері деп оның массасы мен жылдамдық векторының көбейтіндісіне тең (mV) векторлық шаманы айтады. Қозғалыс мөлшерінің векторы әрқашан нүкте жылдамдығымен бағыттас болады. Белгілі уақыт аралығындағы күштің нүктеге әсерін күш импульсі дейді.Күштің элементар импульсі деп күш векторының элементар уақытқа көбейтіндісіне тең векторлық шаманы айтады: Бұл вектор күштің әсер ету сызығының бойымен бағытталады.

50. Нүктенің қозғалыс мөлшерінің өзгеруі туралы теорема. Нүкте үдеуінің векторы жылдамдық векторынан уақыт бойынша алынған бірінші туындыға тең екенін ескерсек,нүкте динамикасының негізгі заңын

былай жазуға болады: теңдеуі нүктенің қозғалыс мөлшерінің өзгеруі туралы теореманыңдифференциалдық түрін береді: нүктенің қозғалыс мөлшерінің уақытбойынша бірінші туындысы нүктеге әсер ететін барлық күштердің геометриялық қосындысына тең.

теңдеуі нүктенің қозғалыс мөлшерінің өзгеруі туралытеореманың интералдық (шекті) түрін береді: шекті уақыт аралығындағы нүктенің қозғалыс мөлшерінің өзгеруі осы уақыт аралығында нүктеге әсер ететін барлық күштер импульстерінің геометриялық қосындысына тең.

51.. Жылдамдықтардың лездік центрі көмегімен жазық-параллель қозғалыстағы дене нүктелерінің жылдамдықтарын анықтау

Дененің кез келген М нүктесінің жылдамдығы полюс ретінде алынған дененің басқа А нүктесінің жылдамдығы мен М нүктесінің полюсті денемен бірге айналғанда алатын жылдамдығының геометриялық қосындысына тең. Теорема: Жазық паралель қозғалыстағы қатты дененің кез келген екі нүктесінің жылдамдықтарының сол нүктелерден өтетін түзуге проекциялары өзара тең7

Дененің (S) қимасының қозғалысында кез келген уақытта жылдамдығы нөлге тең бір нүкте болады. Ол нүктені айналу центрі немесе жылдамдықтардың лездік центрі деп атаймыз.

дене нүктелерінің жылдамдықтары олардың лездік жылдамдықтар центріне дейінгі қашықтықтарына пропорционал болады. Сонымен, 1) Кез келген нүктенің жылдамдығын табу үшін бір нүктенің жылдамдығы (модулі, бағыты) және ізделінді жылдамдықтың бағыты белгілі болуы керек.

2) Лездік жылдамдықтар центрін табу үшін екі нүктенің жылдамдықтарына сол нүктелерде перпендикулярлар құру қажет. Олардың қиылысу нүктесі лездік жылдамдықтар центрін береді

52.Инерция күштері. актив күштері мен Rреакция күші әсер ететін материялық нүктені қарастырайық. Бұл нүкте үшін динамиканың негізгі заңы:

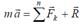түрінде жазылады. Соңғы өрнекті түрлендірейік:

Белгілеу енгізейік: векторы материялық нүктенің инерция күші деп аталады. Оның модулі нүктенің массасы мен үдеуінің көбейтіндісіне тең, ал бағыты үдеу векторына қарама-қарсы болады.

53. Қатты дененің жазық-параллель қозғалысын қарапайым қозғалыстарға жіктеу.

Біз қатты дененің жазық-параллель қозғалысын оның полюспен бірге ілгерілемелі қозғалысы мен полюс төңірегіндегі айналмалы қозғалысының қосындысы деп қарастыруғаболатынын кинематикадан білеміз. Полюс ретінде дененің массалар центрін алған ыңғайлы. Сонда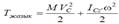

54.Күрделі қозғалыстағы нүктенің үдеулерін қосу туралы теорема

2-буынның (бұлғақтың) В нүктесі үшін үдеулерді қосу туралы теорема түрінде жазылады, мұндағы В нүктесінің А нүктесіне қатысты үдеуінің нормаль құраушысы түрінде анықталады және векторы АВ кесіндісіне параллель В нүктесінен А нүктесіне қарай бағытталған, ал жанама құраушы – АВ кесіндісіне перпендикуляр.(41-сурақ)

Дата добавления: 2017-01-14