Остойчивость на больших углах крена. Диаграмма статической остойчивости. Особенности диаграммы

При больших наклонениях моменты инерции равнообъемных ватерлиний изменяются с углом крена. Соответственно изменя­ются и радиусы кривизны траектории центра величины, которая будет отличаться от окружности, положенной в основу при выво­де метацентрической формулы остойчивости. Указанное обстоя­тельство существенно меняет зависимость восстанавливающего момента от угла крена. Установление этой зависимости и являет­ся первой задачей при изучении остойчивости при больших углах крена.

Если кренящая пара наклоняет судно на большой угол, то траектория центра величины не лежит в поперечной плоскости. Вследствие несимметрии носовой и кормовой оконечностей появ­ляется смещение центра величины в продольном направлении и пара, образуемая весом судна и силой поддержания, не будет совпадать с плоскостью кренящей пары. Разлагая образующуюся пару на составляющие в поперечной и продольной плоскостях, получим, что поперечная составляющая уравновесит кренящую пару, а продольная вызовет наклонение судна в продольном на­правлении. Момент этой продольной составляющей пары назы­вается деривационным моментом. При обычной форме обводов дифферент, вызванный деривационным моментом, оказывается малым, им пренебрегают и рассматривают не действительную пространственную траекторию центра величины, а ее проекцию на плоскость наклонения. Эта проекция траектории ЦВ называет­ся кривой центра величины (кривой С).

ДСО. Зависимость плеча восстанав­ливающего момента от угла крена изображают в прямоугольных координатах, откладывая по оси абсцисс углы крена в градусах, а по оси ординат — плечи остойчивости в метрах. Кривая, пред­ставляющая эту зависимость, называется диаграммой статичес­кой остойчивости или диаграммой Рида. Поскольку диаграмма строится для постоянного водоизмещения, она же изображает зависимость восстанавливающего момента от угла крена, для чего масштаб момента можно также нанести на оси орди­нат. Диаграмма статической остойчивости изображена на рис. 4.5.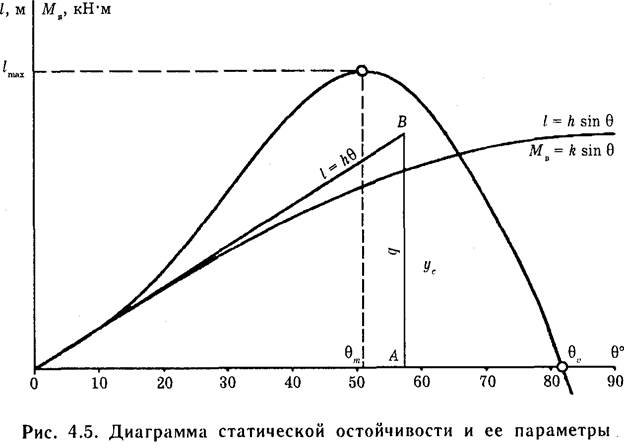

Ввиду симметрии формы судна диаграмма строится только для положительных углов крена (на правый борт). При крене на противоположный борт (ϴ<0) диаграмма продолжается как не­четная функция:

Характерными параметрами диаграммы являются: крутизна начального участка, максимальное плечо остойчивости lmах, угол максимума диаграммы ϴт, угол заката диаграммы ϴv (при котором плечо остойчивости обращается в нуль), площадь, ограниченная кривой и осью абсцисс. Эти параметры характеризуют остойчи­вость на больших углах крена.

4.Определение угла крена по диаграмме при заданном .

При решении будем пользоваться диаграммой, построенной в моментах. Если диаграмма построена в плечах, то вместо креня­щего момента M_кр следует использовать кренящее плечо l_кр, при­веденное к масштабу диаграммы делением кренящего момента на водоизмещение:

Допустим, что на судно действует внешний кренящий момент M_кр, не зависящий от угла крена. Положение равновесия найдет­ся из условия равенства кренящего и восстанавливающего мо­ментов. Для определения угла крена отложим по оси ординат диаграммы отрезок ОС, равный, в масштабе моментов, величине М и проведем горизонталь СА до пересечения с диаграммой на рис. 4.7. Тогда угол ϴ_a и будет искомым углом крена судна. Формально имеется второе решение, определяемое точкой В, однако оно не имеет практического значения, так как момент M_кр не накренит судно до угла ϴ_b. Кроме того, точке А, лежащей на восходящей ветви диаграммы, соответствует устойчивое положе­ние равновесия, а точке В, лежащей на нисходящей ветви, — неустойчивое положение равновесия. Действительно, наклоним судно из положения А на дополнительный малый угол δϴ и отпу­стим его, тогда ставший избыточным восстанавливающий момент вернет судно в начальное положение А. Если уменьшить угол крена на δϴ, то избыток кренящего момента опять вернет судно в положение A. Таким образом, судно возвращается к равно­весию при угле ϴ_a в какую бы сторону мы его не отклонили. Значит, положение А есть устойчивое положение равновесия. Наклоним дополнительно теперь судно из положения В. Тогда появится избыток кренящего момента, который будет еще боль­ше кренить судно и оно опрокинется. Если же уменьшить угол крена, то избыток восстанавливающего момента переведет судно в положение A. В обоих случаях судно уходит от положения рав­новесия, определяемого точкой В, значит это положение равнове­сия неустойчивое.

Нетрудно видеть, что при действии постоянного кренящего момента устойчивому положению равновесия соответствует вся восходящая ветвь диаграммы.

5.Определить по диаграмме при заданном угле крена.

Обратная задача — определение действующего кренящего мо­мента по углу крена судна для случая постоянного момента реша­ется обратным построением. По оси абсцисс откладываем извес­тный угол крена, проводим вертикаль до пересечения с диаграм­мой и через полученную точку — горизонталь до оси ординат, по которой прочитываем значение действующего момента. Если при отложенном угле крена диаграмма пересекается с осью абсцисс, то крен судна является следствием отрицательной начальной остойчивости, а не воздействия внешнего кренящего момента.

6.Определить статический опрокидывающий момент по диаграмме .

Третья задача — определение наибольшего выдерживаемого судном кренящего момента решается измерением в масштабе шкалы моментов наибольшей ординаты диаграммы статической остойчивости. Если диаграмма построена в плечах остойчивости, то наибольший момент найдется по формуле = Р1_max, где 1_max — наибольшая ордината диаграммы. Абсцисса максимума диаг­раммы ϴ_m определит наибольший угол крена, до которого судно может быть наклонено постоянным моментом, не опрокидывая его.

7.Свойство касательной к диаграмме при .

Свойством касательной пользуются для уточнения начального участка диаграммы. Для построения касательной на рис. 4.5 по оси абсцисс откладывают отрезок ОА, равный одному радиану (57,3°), а по перпендикуляру к оси — отрезок АВ, равный h₀. Прямая ОB и будет касательной к диаграмме в начале координат. Возможно и обратное использование свойства касательной — для определения по диаграмме начальной метацентрической высоты. Однако, ввиду погрешности при графическом проведении каса­тельной и погрешности в построении диаграммы, такой способ не может обеспечить хорошей точности определения метацентричес­кой высоты.

Уравнение касательной как прямой, исходящей из начала ко­ординат с угловым коэффициентом h₀, в осях ϴ и l имеет вид: 1 = h₀ϴ, т.е. изображает зависимость плеча остойчивости, да­ваемую линейной метацентрической формулой остойчивости. На том же рис. 4.5 изображена синусоидальная метацентрическая формула: 1 = h sinϴ. Из рисунка видно, что при малых углах крена все три зависимости близки между собой и можно пользо­ваться простейшей из них — линейной. С увеличением угла крена погрешность метацентрических формул становится существен­ной, а далее — недопустимой.

Диапазон углов применимости метацентрических формул зависит от вида диаграммы статической остойчивости и требуемой точности. Практически принято ими пользоваться до углов крена 10—12°.

Дата добавления: 2017-01-14