Пример 2. Перевод целого числа из десятичной системы в любую другую позиционную систему

Пример 1. Перевод целого числа из любой позиционной системы счисления в десятичную.

Любое число можно представить в развернутом виде:

A_m-1*P^m-1+ A_m-2*P^m-2 + …+A₁*P¹ + A₀*P⁰ + A_-1*P^-1 +…+A_-s*P^-s, где

P – основание системы счисления,

m – положительные значения индексов для целой части числа,

s – отрицательные значения индексов для дробной части числа.

Правило: Для того чтобы число из любой системы счисления перевести в десятичную систему счисления, необходимо его представить в развернутом виде и произвести вычисления.

1101₍₂₎= 1*2³ + 1*2²+0*2¹+ 1*2⁰=13₍₁₀₎;

112₍₃₎= 1*3²+ 1*3¹ +2*3⁰=14₍₁₀₎;

341,5₍₈₎=3*8²+ 4*8¹ +1*8⁰ +5*8^-1=225,625₍₁₀₎;

A1F,4₍₁₆₎= A*16² + 1*16¹ + F*16⁰ + 4*16^-1=2591,25₍₁₀₎

Правило перевода целых чисел из десятичной системы счисления в систему с основанием «P»:

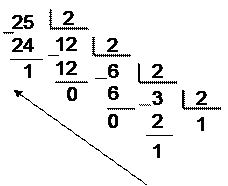• Последовательно выполнять деление исходного числа и получаемых частных на «P» до тех пор, пока не получим частное, меньшее делителя.

• Полученные при таком делении остатки – цифры числа в системе счисления «P» – записать в обратном порядке (снизу вверх).

Переведем число 25₍₁₀₎ в двоичную систему.

Ответ: 25₍₁₀₎=11001₍₂₎

Пример 3. Перевод дробного числа из десятичной системы в любую другую позиционную систему.

Правило перевода дробных чисел из десятичной системы счисления в систему с основанием «P»:

• Последовательно выполнять умножение исходного числа и получаемых дробные части на «P» до тех пор, пока дробная часть не станет равна нулю или не достигнем требуемую точность.

• Полученные при таком умножении целые части - числа в системе счисления «P» – записать в прямом порядке (сверху вниз).

Переведем число 0,5625₍₁₀₎ в двоичную систему.

0,5625*2= 1,125

0,125*2= 0,25

0,25*2= 0,5

0,5*2= 1,0

Ответ: 0,5625₍₁₀₎₎=0,1001₍₂₎

Пример 4. Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему.

Правило перевода: необходимо каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

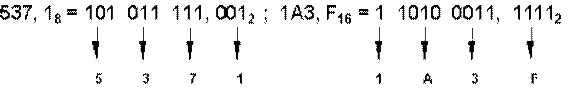
Пример 5. Перевод числа из двоичной системы в восьмеричную или шестнадцатеричную

Правило перевода: число нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

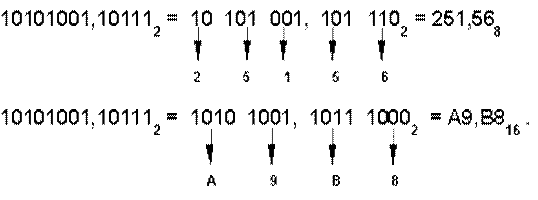
Сводная таблица переводов целых чисел

Дата добавления: 2017-01-14