Соотношение между единицами давления

Единица	Па	кгс/м^2	ат(кгс/см^2)	мм вод.ст	мм рт. ст.
1 Па		0,102	0,102 ^.10^-4	0,102	7,50 ^.10^-3
1 кгс/м^2	9,8		10^-4		73,56 ^.10^-3
1 кгс/см^2	9,8 ^.10^4	10^4		10^4	735,56
1 мм вод.ст	9,8		10^-4		73,56 ^.10^-3
1 мм рт.ст	133,32	13,59	13,59	13,59

Давление можно также измерять высотой столба жидкости (обычно ртути или воды). Техническая атмосфера соответствует 735,6 мм рт. ст. при температуре ртути 0⁰ С или 10 м вод. ст. Так называемая физическая атмосфера (атм), или стандартное атмосферное давление, сохраняет свое значение и при пользовании системой СИ и соответствует 760 мм рт. ст. при температуре ртути 0⁰С или 10332 мм вод. ст. В системе СИ давление измеряется в Па (1Па=1Н/м²).

Удельный объем вещества представляет собой объем, занимаемый единицей массы этого вещества.

υ = V/M, (5.2)

где υ – удельный объем, м³/кг; V – объем тела, м³; М – масса тела, кг.

При измерении температуры пользуются термометрами различных типов и двумя основными температурными шкалами: шкалой Цельсия и абсолютной (шкалой Кельвина). Связь между абсолютной температурой и температурой по шкале Цельсия выражается формулой:

T = t + 273, (5.3)

где Т – абсолютная температура, К; t – температура по шкале Цельсия, °С.

Для сравнения различных газов между собой по объему их приводят к так называемым нормальным физическим условиям (НФУ), характеризующимся давлением Р = 760 мм рт. ст. (101325 Па) и температуройt = 0°С (273 К).

Основные параметры газа связаны между собой функциональной зависимостью, называемой уравнением состояния:

F (P, υ, T) = 0. (5.4)

Наиболее простым уравнением состояния является уравнение Клапейрона для идеального газа:

РV = MRT, (5.5)

где Р – абсолютное давление газа, Па; V – объем газа, м³; М – масса газа,кг; R – газовая постоянная, Дж/(кг·К); Т – абсолютная температура, К.

Для 1 кг газа уравнение (1.5) имеет вид:

Pυ = RT, (5.6)

где υ – удельный объем, м³/кг.

Газовая постоянная R представляет собой физическую постоянную, которая для каждого газа принимает своё определенное значение, зависящее от природы газа и не зависящее от его состояния.

Уравнение (5.6) можно записать для 1 кмоль газа, умножая обе части уравнения на молекулярную массу µ:

pυ_μ = µRT или pVµ = µRT, (15.7)

где µ – молекулярная масса (число кг в 1 кмоль), (прил 3), кг/кмоль; Vµ – объем 1 кмоль, м³/кмоль; µR – универсальная газовая постоянная, Дж/(кмоль·К).

Универсальная газовая постоянная µR не зависит от состояния газа и одинакова для всех идеальных газов. Значение µR можно определить из уравнения (15.7), записывая его для НФУ (нормальных физических условий), при которых υ_μ любого идеального газа равен 22,4 м3/ кмоль (следствие из закона Авогадро):

µR = 8314 Дж/(кмоль·К).

Зная универсальную газовую постоянную µR, можно подсчитать газовую постоянную R, которую иногда, в отличие от универсальной,называют удельной:

, Дж/(кг·К). (5.8)

Пользуясь характеристическим уравнением для двух различных состояний, какого либо газа, можно получить выражение для определения любого параметра при переходе от одного состояния к другому, если значения остальных параметров известны:

, (5.9)

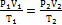. (5.10)

Уравнения (5.9) и (5.10) часто применяют для «приведения объема к нормальным условиям», т. е. для определения объема, занимаемого газом, при t = 0⁰Cиp = 760 мм рт. ст., если объем его при каких-либо значениях P и t известен. Для этого случая уравнение (5.10) обычно представляют в следующем виде:

(5.11)

В правой части уравнения все величины взяты при нормальных условиях, в левой – при произвольных значениях давления и температуры.

Уравнение (1.9) можно переписать следующим образом:

,

следовательно,

ρ₂ = ρ₁ , (5.12)

где ρ₁ и ρ₂- плотности при двух состояниях вещества,кг/м³.

Уравнение (5.12) позволяет определить плотность газа при любых условиях, если значение его для определенных условий известно.

Дата добавления: 2017-01-14