Соотношение неопределенностей Гейзенберга

В.Гейзенберг, учитывая волновые свойства микрочастиц и связанные с волновыми свойствами ограничения в их поведении, пришел в 1927 г. к выводу, что объект микромира невозможно одновременно с любой наперед заданной точностью харак­теризовать и координатой и импульсом. Согласно соотношению неопределенностей Гейзенберга, микрочастица не может иметь одновременно и определен­ную координату (х, у, z), и определенную соответствующую проекцию импульса (р _х, р_у, p_z), причем неопределенности этих величин удовлетворяют условиям: , , , 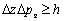(2.1)

где  x,  у,  z – неопределенности координат частицы, а , , 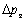- неопределенности компонент импульса. Произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h. То есть,чем точнее мы знаем координату, тем менее определена проекция импульса и наоборот. Отсюда вытекает и фактическая невозможность одновременно с любой, наперед заданной точностью измерить координату и импульс микрообъекта.

Так как электроны обладают волновыми свойствами, то при их прохождении через щель, размер которой сравним с длиной волны де Бройля  электрона, наблюдается дифракция. Дифракционная картина, наблюдаемая на экране (Э), характеризуется главным максимумом, расположенным симметрично оси Y, и побочными максимумами по обе стороны от главного (их не рассматриваем из-за незначительной интенсивности по сравнению с главным максимумом).

До прохождения через щель электроны двигались вдоль оси Y, поэтому составляющая импульса р _х=0, так что =0, а координата х частицы является совершенно неопределенной. В момент прохождения электронов через щель их положение в направление оси Х определяется с точностью до ширины щели, т.е. с точностью  х. В этот же момент вследствие дифракции электроны отклоняются от первоначального направления и будут двигаться в пределах угла 2( – угол, соответствующий первому дифракционному минимуму). Следовательно, появляется неопределенность в значении составляющей импульса вдоль оси Y, которая, как следует из рис.2.1 и формулы (1.2), равна . (2.2)

Ограничимся рассмотрением электронов, попадающих на экран в пределах главного максимума. Из теории дифракции известно, что первый минимум соответствует углу , удовлетворяющему условию

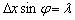, (2.3)

где  х –ширина щели, а  – длина волныде Бройля. Из формул(2.2) и (2.3) получим ,

где учтено, что для некоторой незначительной части электронов, попадающих за пределы главного максимума, . Следовательно, получаем выражение , то есть соотношение неопределенностей (2.1).

Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты, импульса) и наличия у нее волновых свойств. Оно является квантовым ограничением применимости классической механики к микрообъектам и позво­ляет оценить, например, в какой мере можно применять понятия классической меха­ники к микрочастицам, в частности, с какой степенью точности можно говорить о траекториях микрочастиц. Известно, что движение по траектории характеризуется в любой момент времени определенными значениями координат и скорости. Выразим соотношение неопределенностей (2.1) в виде

(2.4)

В квантовой теории рассматривается также соотношение неопределенностей для энергии Е и времени t, т.е. неопределенности этих величин удовлетворяют условию

(4.5)

где  Е – неопределенность энергии некоторого состояния системы,  t – промежуток времени, в течение которого оно существует. Следовательно, систе­ма, имеющая среднее время жизни  t, не может быть охарактеризована определенным значением энергии; разброс энергии  Е = h / t возрастает с уменьшением среднего времени жизни. Из выражения (4.5) следует, что частота излученного фотона также должна иметь неопределенность   = Е / h, т.е. линии спектра должны характеризо­ваться частотой, равной  ± Е / h. Опыт действительно показывает, что все спектраль­ные линии размыты; измеряя ширину спектральной линии, можно оценить порядок времени существования атома в возбужденном состоянии.

59. Волновые свойства микрочастиц. Волновая функция и её статистический смысл.

Дифракционная картина для микрочастиц является проявлением статистичес­кой (вероятностной) закономерности, согласно которой частицы попадают в те места, где интенсивность волн де Бройля наибольшая.

Можно ли волны де Бройля истолковывать как волны вероятности, т. е. считать, что вероятность обнаружить микрочастицу в различных точках пространства меняется по волновому закону? Такое толкование волн де Бройля уже неверно хотя бы потому, что тогда вероятность обнаружить частицу в некоторых точках пространства может быть отрицательна, что не имеет смысла.

Немецкий физик М. Борн (1882—1970) в 1926 г. предположил, что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначаемая Y(х, у, z, t). Эту величину называют также волновой функцией (или Y-функцией). Амплитуда вероятности может быть комплексной, и вероятность W пропорциональна квадрату ее модуля:

(1.1)

(|Y|²=YY*, Y * — функция, комплексно сопряженная с Y). Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероят­ностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент време­ни t в области с координатами х и x+dx, у и y+dy, z и z+dz.

Итак, в квантовой механике состояние микрочастиц описывается принципиально по-новому — с помощью волновой функции, которая является основным носителем информации об их корпускулярных и волновых свойствах. Вероятность нахождения частицы в элементе объемом d V равна

(1.2)

Величина

(квадрат модуля Y-функции) имеет смысл плотности вероятности, т. е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с коор­динатами х, у, z. Таким образом, физический смысл имеет не сама Y-функция, а квадрат ее модуля |Y|², которым задается интенсивность волн де Бройля.

Вероятность найти частицу в момент времени t в конечном объеме V, согласно теореме сложения вероятностей, равна

Так как |Y|²d V определяется как вероятность, то необходимо волновую функцию Y нормировать так, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Это означает, что при данном условии частица должна находиться где-то в пространстве. Следовательно, условие нормировки вероятностей

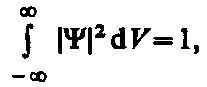(1.3)

где данный интеграл (1.3) вычисляется по всему бесконечному пространству, т. е. по координатам х, у, z от –¥ до ¥. Таким образом, условие (1.3) говорит об объективном существовании частицы в пространстве.

Чтобы волновая функция являлась объективной характеристикой состояния микро­частиц, она должна удовлетворять ряду ограничительных условий. Функция Y, харак­теризующая вероятность обнаружения действия микрочастицы в элементе объема, должна быть конечной (вероятность не может быть больше единицы), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком).

Дата добавления: 2017-01-14