Регулирование скорости вращения двигателей постоянного тока

§ 116 РЕГУЛИРОВАНИЕ СКОРОСТИ ВРАЩЕНИЯ ДВИГАТЕЛЕЙ ПОСТОЯННОГО ТОКА

Двигатели постоянного тока дают возможность плавно и эконо­мично регулировать скорость вращения в широких пределах. В результате этого весьма ценного свойства двигатели постоянного тока получили широкое распространение и часто являются неза­менимыми.

Число оборотов якоря двигателя при любой схеме возбуждения определяется следующим выражением:

где rс — сопротивление последовательной обмотки возбуждения (для двигателя параллельного возбуждения rс=0). Это выраже­ние показывает, что изменение скорости вращения двигателя мож­но осуществить изменением напряжения сети, сопротивления цепи якоря и магнитного потока.

Регулирование скорости вращения изменением напряжения сети осуществляется в случае, когда источником электрической энергий двигателя является какой-либо генератор.

Для регулирования скорости вращения двигателя изменением сопротивления цепи якоря используется регулировочный реостат, включенный последовательно с якорем. В отличие от пускового ре­гулировочный реостат должен быть рассчитан на длительное про­хождение тока. В сопротивлении регулировочного реостата происходит большая потеря энергии, вследствие чего резко уменьшается

п. д. двигателя.

Регулирование скорости вращения якоря двигателя изменением магнитного потока производится изменением тока в обмотке воз­буждения. В двигателях параллельного и смешанного возбуждения включается регулировочный реостат. В двигателях последователь­ного возбуждения изменение тока в обмотке возбуждения дости­гается шунтированием этой обмотки каким-либо регулируемым со­противлением. Этот способ регулирования скорости не создает до­полнительных потерь и экономичен.

Регулирование скорости двигателей постоянного тока, как видно из формулы (8.3), может быть достигнуто следующими способами: введением сопротивления в цепь якоря; изменением магнитного потока; изменением напряжения, подводимого к двигателю

12 Механические характеристики.
Механические характеристики двигателей принято подразделять на естественные и искусственные. Естественная характеристика соответствует номинальному напряжению питания и отсутствию добавочных сопротивлений в цепях обмоток двигателя. Если хотя бы одно из перечисленных условий не выполняется, характеристика называется искусственной.
Уравнения электромеханической ω=f(I я) и механической ω=f(M эм.) характеристик могут быть найдены из уравнения равновесия ЭДС и напряжений для якорной цепи двигателя, записанного на основании второго закона Кирхгофа:

U я=E я+I я)(R я+R д), (5.35)

где R я – активное сопротивление якоря.
Преобразуя (5.35) с учетом (5.6), получим уравнение электромеханической характеристики

ω=(U я-I я(R я+R д))/kФ. (5.36)

В соответствии с (5.10) ток якоря I я=M эм./kФ и выражение (5.36) преобразуется в уравнение механической характеристики:

ω=Uя/ kФ – (R я+ R д)/(kФ) 2)Mэм.. (5.37)

Это уравнение можно представить в виде ω= ω о.ид.- Δ ω, где

ω о.ид.=Uя/kФ (5.38)

ω о.ид - угловая скорость идеального холостого хода (при Iя=0 и, соответственно, Мэм.=0); Δ ω= Мэм.[(Rя+Rд)/(kФ)2]– уменьшение угловой скорости, обусловленное нагрузкой на валу двигателя и пропорциональное сопротивлению якорной цепи.
Семейство механических характеристик при номинальном напряжении на якоре и потоке возбуждения и различных добавочных сопротивлениях в цепи якоря изображено на рис. 5.20,а.

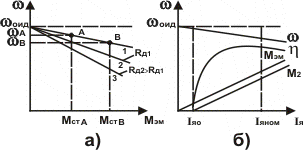
Рис.5.20

Механические характеристики двигателей принято оценивать по трем показателям: устойчивости, жесткости и линейности.
Естественная механическая характеристика, соответствующая (5.37) при Rд=0, изображена прямой линией 1. Механическая характеристика линейная; отклонение от линейного закона может быть вызвано реакцией якоря, приводящей к изменению потока Ф. Эта характеристика жесткая, так как при изменении момента нагрузки и соответственно скорости поток возбуждения не изменяется. Жесткость характеристики уменьшается при введении добавочного сопротивления в цепь якоря (прямые линии 2 и 3 – искусственные реостатные характеристики). Характеристики устойчивые, так как dω/dMэм.<0, и обеспечивают саморегулирование двигателя, т.е. он автоматически приспосабливается к изменяющейся нагрузке. Увеличение статического момента сопротивления на валу двигателя приводит к уменьшению угловой скорости и ЭДС якоря. Ток якоря, выражение для которого можно записать на основании (5.35),

Iя= (Uя-Eя)/(R я+ R д)=(Uя -kωФ;)/(R я R д), (5.39)

возрастает. Соответственно растет электромагнитный момент вплоть до нового значения момента сопротивления (переход из точки А в точку В на механической характеристике).
По аналогии на основании (5.37) может быть построено семейство искусственных характеристик при различных значениях Uя или Ф. Анализ таких характеристик будет проделан в разделе исполнительных двигателей постоянного тока (§ 5.7)

Дата добавления: 2017-01-14