Теорема Кронекера – Капеллі

Ранг матриці.

Метод Гаусса.

Матричний метод.

а₁₁ а₁₂ … а_1n x₁ b₁

а₂₁ а₂₂ … а_2n x₂ b₂

Нехай А = … … … …, Х = …, B = …

а_n1 а_n2 … а_nn x_n b_n

Матриця А називається основною. Тоді систему можна записати матричним рівнянням

А ∙Х = В

Якщо матриця А має обернену матрицю А^-1, то Х = А^-1 ∙ В.

Суть метода Гаусса полягає в тому, що послідовним виключенням змінних система рівнянь перетворюється у еквівалентну їй ступінчату або трикутну систему, яка розв’язується у зворотньому напрямі. Якщо записати розширену матрицю системи, то можна працювати тільки з коефіцієнтами матриці, зводячи її до трапецієвидного виду, причому нульові рядки, що з’являються при зведенні, відкидаються, а суперечливі рядки зупиняють процес зведення (система буде несумісною).

Методом Гаусса можна розв’язувати будь-які системи, у яких число рівнянь не співпадає з числом невідомих (основна матриця системи не квадратна). У випадку сумісної системи ми можемо знайти і єдиний і безліч розв’язків. Однорідні системи теж можна розв’язувати методом Гаусса,

якщо визначник основної матриці системи дорівнює нулю (якщо ∆ ≠ 0, то система буде мати єдиний тривіальний, тобто нульовий, розв’язок).

Рангом r (А) матриці А називається найбільший з порядків її мінорів, відмінних від нуля.

Два способи обчислення ранга матриці:

1) досліджуються мінори першого, другого,....., k – го порядку доти, поки не станеться одне з двох: або всі мінори порядку k дорівнюють нулю, або мінор порядку k не існує, тоді r(А) = k – 1.

2) цей метод базується на тому, що ранг матриці не змінюється, якщо над матрицею виконати так звані елементарні перетворення, а саме:

а) переставити місцями два рядки (стовпці);

б) помножити кожен елемент рядка (стовпця) на один і той самий відмінний від нуля множник;

в) додати до елементів рядка (стовпця) відповідні елементи другого рядка(стовпця), помножені на одне і те саме число.

Елементарні перетворення виконуються доти, поки в кожному рядку і в кожному стовпчику залишиться не більше одного ненульового елемента. Ранг матриці дорівнює числу цих ненульових елементів. Матрицю можна звести до ступінчатого (трапецієвидного) виду, використовуючи тільки елементарні перетворення з рядками, тоді число ненульових рядків і буде рангом матриці.

Для того, щоб система лінійних рівнянь була сумісною, необхідно і достатньо, щоб ранг її основної матриці дорівнював рангу розширеної матриці, тобто r(A) = r(A), де A - розширена матриця, яка утворюється з основної шляхом приписування до неї стовпчика вільних членів.

Завдання №1:

а) обчислити суму, різницю та добуток матриць А (табл. 1.1) та В (табл.1.2);

б) для матриць А та В виконати дії: (2А - 3В) · (3А + 2В);

в) перевірити рівність Δ А·Δ В = Δ (А·В), використавши різні способи обчислення

визначників (метод трикутників, метод Саррюса, теорему 1);

г) для матриць А та В знайти обернені матриці А^-1 та В^-1, зробити перевірку та обчислити

вираз (А^-1 + В^-1)²;

д) обчислити визначник та ранг матриці четвертого порядку (табл.1.4).

.

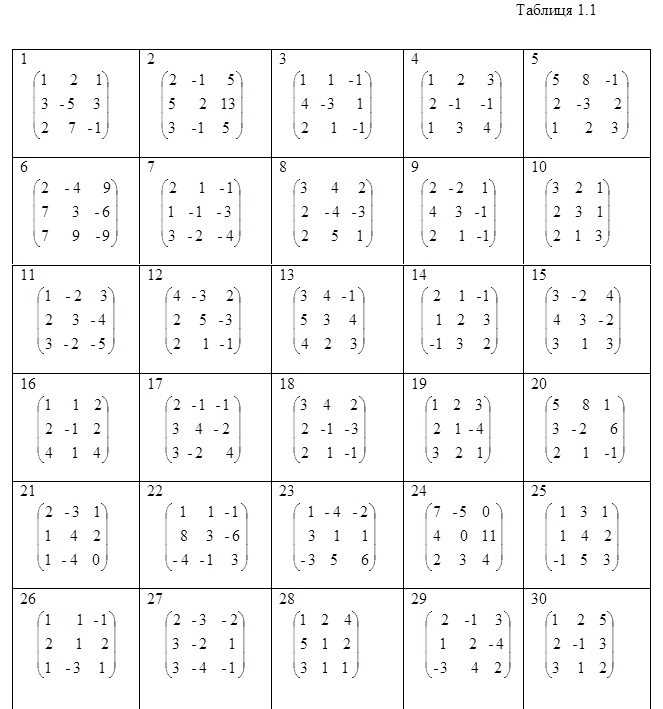Завдання № 2. Розв'язати систему лінійних рівнянь (табл.1.3) методом Крамера (методом

визначників), методом оберненої матриці та методом Гаусса, порівняти результати.

Завдання №3. Розв'язати систему лінійних рівнянь 4-го порядку методом Гаусса, виписавши

розширену матрицю системи і зводячи її до трапецієвидного (або трикутного) виду, застосувавши елементарні перетворення з рядками матриці.

Зворотнім ходом відновити систему і знайти її розв'язки.

Таблиця 1.3

1

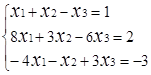
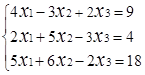
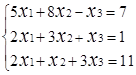
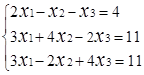
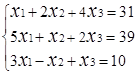
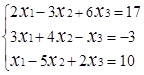
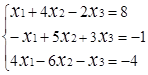
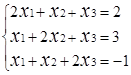
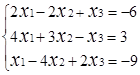
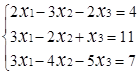
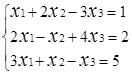
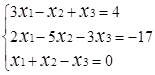
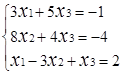
Системи 4-го порядку

1). x₁ + 3x₂ – x₃ + 5x₄ = 6

2x₁ – 2x₃ + x₄ = –6

2x₂ + x₃ – 3x₄ = –1

–x₂ +2x₄ = 4

2). 3x₁ + 2x₂ – x₃ – x₄ = –8

–x₂ + 3x₄ = 9

5x₁ – 2x₃ + x₄ = –6

3x₃ – 2x₄ = 0

3). x₁ + 3x₂ – 5x₄ = –16

2x₂ + 3x₃ + 4x₄ = 18

4x₁ – 3x₄ = –13

–3x₃ + 2x₄ = 0

4). 5x₂ + x₃ – 3x₄ = –1

x₁ – 3x₂ + x₃ = 6

5x₂ + 2x₃ – 3x₄ = 4

2x₂ + x₄ = 2

5). x₁ + 3x₃ – 2x₄ = –3

x₂ – 5x₃ + 3x₄ = 9

4x₃ + 2x₄ = 4

3x₁ – 4x₂ + 3x₄ = –3

6). 5x₁ – x₂ + 5x₃ – x₄ = 0

2x₂ + 3x₄ = 12

3x₁ – 5x₃ + x₄ = 5

4x₂ – x₃ – 3x₄ = 6

7). 4x₁ – x₄ = 2

2x₂ + 3x₃ – 4x₄ = 7

5x₁ + 5x₂ – 3x₃ + 3x₄ = –4

x₁ + 2x₂ + 3x₃ = 16

8). 3x₂ – 2x₃ + x₄ = –1

2x₁ + x₂ + x₃ + 2x₄ = 6

3x₃ + x₄ = 9

5x₁ – 2x₃ + x₄ = –6

9). 5x₁ + 2x₂ – x₃ = 11

2x₂ – 5x₃ – 2x₄ = 2

x₁ + x₂ + 3x₃ + 2x₄ = 8

x₃ – x₄ = - 2

10). 5x₁ + x₂ – 2x₃ + 2x₄ = –1

3x₂ – 3x₃ + 5x₄ = –5

2x₂ – x₄ = - 2

2x₁ – 2x₃ + 4x₄ = 0

11). 2x₁ – x₂ + 3x₃ – x₄ = –6

x₁ + x₂ + x₄ = 9

3x₁ – 2x₃ = 8

5x₂ + 3x₃ = 12

12). x₁ – 2x₂ + x₄ = 0

2x₁ + x₂ – x₃ – 3x₄ = –4

x₁ – 3x₂ – 5x₃ + x₄ = 2

2x₂ + x₃ – 4x₄ = –11

13). x₁ – 2x₂ + 3x₃ – x₄ = –11

2x₁ + 4x₃ = 0

–3x₂ + x₃ + 2x₄ = –2

3x₁ – x₂ + 2x₄ = 11

14). 4x₁ + 2x₃ – 4x₄ = –10

2x₁ + 3x₂ + 5x₃ = 8

x₁ + 2x₂ – x₃ + 3x₄ = 21

5x₂ + 4x₃ – 2x₄ = 3

15). 2x₁ – 3x₂ + x₃ + 2x₄ = 8

–x₁ + 4x₃ + 3x₄ = –3

3x₂ + x₃ – 2x₄ = –4

–2x₁ + x₂ – x₃ + 3x₄ = –12

16). 4x₁ – 3x₃ + x₄ = –1

2x₁ + 2x₂ – 4x₄ = 4

x₁ + x₂ + 3x₃ – x₄ = 3

–5x₂ + 3x₃ + 5x₄ = 8

17). 3x₁ – 2x₃ = 1

x₁ + 2x₂ – x₃ + 3x₄ = –12

–x₁ – x₂ + 4x₃ – 2x₄ = 10

3x₂ – 4x₄ = –1

18). x₁ – 2x₂ + x₃ + x₄ = –1

–x₁ + 3x₂ – 4x₄ = –9

2x₁ – x₂ + 2x₃ + x₄ = –2

5x₂ + 2x₃ = 1

22). 2x₁ + x₂ – x₃ + x₄ = 8

2x₂ + x₃ – x₄ = –3

3x₁ – x₂ + 2x₄ = 21

2x₂ + x₄ = 2

23). x₁ + 2x₂ + x₃ = 2

2x₃ – 2x₄ = 2

2x₁ + 3x₂ – 4x₃ + 5x₄ = –4

3x₂ – x₄ = –2

24). x₁ –2x₂ + x₃ + x₄ = 4

x₁ – 2x₃ + 2x₄ = 3

4x₁ + x₃ – x₄ = 3

2x₁ + 2x₂ + x₄ = 10

25). x₁ - x₄ = 0

2x₂ + x₃ – x₄ = –3

3x₁ – x₂ + 2x₄ = 21

2x₂ + x₄ = 2

19). 2x₁ – x₂ + 3x₃ – x₄ = –10 26). 2x₁ – 3x₄ = – 4

–x₁ + 2x₂ – x₃ + 2x₄ = 10 3x₁ + x₂ + 3x₃ – 3x₄ = 8

2x₂ + x₃ + x₄ = 3 x₂ + x₃ + x₄ = 6

x₁ + 2x₂ – 2x₃ – x₄ = 3 3x₂ + x₃ + x₄ = 4

20). x₁ – 2x₂ + x₃ = –4 27). 3x₂ + x₃ + x₄ = 4

–x₁ + 2x₂ – 2x₄ = 0 2x₁ – 3x₂ + x₄ = 15

3x₂ – x₃ – 2x₄ = 3 2x₂ + x₃ = 1

x₁ – 2x₃ = 4 x₁ – 2x₄ = –4

21). x₁ – x₂ + x₃ – x₄ = –2 28). x₁ – x₂ + x₃ – x₄ = –2 x₁ – 2x₃ + 2x₄ = 3 2x₁ + x₃ – x₄ = 1

4x₁ + x₃ – x₄ = 3 x₁ – x₂ + 2x₃ – x₄ = 1

5x₁ + 2x₂ + x₄ = 13 x₂ +2 x₃ – x₄ = 4

Таблиця 1.4

ПРИКЛАД 1. Обчислити визначник та ранг матриці четвертого порядку.

А= ΔА = 1· А₁₁+1· А₁₂ -1· А₁₃ +1· А₁₄

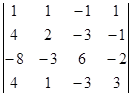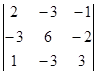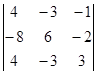А= =1· -1· 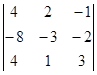-1· - 1·

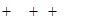
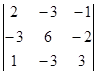
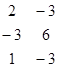=36+6-9+6-12-27=0

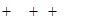
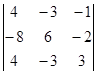
=24*3+24-24+24-24-72=0

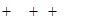
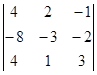
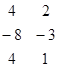=-36-16+8-12+8+48=0

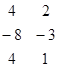=36+48-24-36-24+24-24=0

ΔА=0, тобто ранг < 4. Визначимо ранг зведенням до ступінчатого виду:

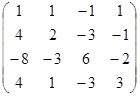
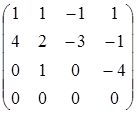
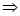
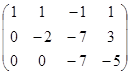. Висновок: ранг = 3.

Дата добавления: 2017-01-14