КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интернет-ресурсы 1 страница
|
|
|
|
ПРИКЛАД 2.
Розв’язати систему лінійних рівнянь методом Крамера (метод визначників), методом Гаусса та матричним, порівняти результати.

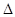 =
= 
 =32+6+6+12-8+12=60;
=32+6+6+12-8+12=60;

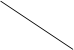




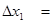

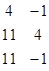 =64+22+22+44-16+44=180;
=64+22+22+44-16+44=180;






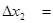

 =88-24-33+33+44-12*4=88-20-48=60;
=88-24-33+33+44-12*4=88-20-48=60;








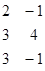 =88-33-24-16*3+44+33=88-28=60;
=88-33-24-16*3+44+33=88-28=60;
x  =
=  =
=  =3 x
=3 x  =
=  =
=  =1 x
=1 x  =
=  =
=  =1
=1
Перевірка
2·3-1-1=4 4=4
3·3+4-2=11 11=11
3·3-2+4=11 11=11
Метод Гаусса:




















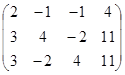

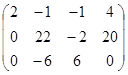
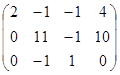
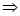





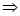
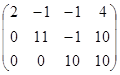 ; 10х3=10 x3=1; 11 x2 - х3=10 x2=1;
; 10х3=10 x3=1; 11 x2 - х3=10 x2=1;
2 x1- х2 -х3 =4 x1 = 3.
Метод оберненої матриці
А= 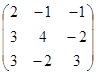 ;
; 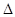 =60
=60
А 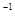 =
=  ·
· 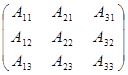
x= 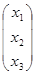 ; b=
; b= 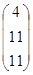 ; X= А
; X= А 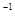 ·b
·b
А  =
=  = 16-4= 12 А
= 16-4= 12 А  = -
= -  = -(-4-2)=6
= -(-4-2)=6
А  = -
= -  = -(12 + 6)= -18 А
= -(12 + 6)= -18 А  =
=  =8+3=11
=8+3=11
А  =
= 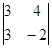 = -6 -12= -18 А
= -6 -12= -18 А  = -
= -  =1
=1
А  =
=  = 2+4= 6
= 2+4= 6
А  = -
= -  = +4-3= 1
= +4-3= 1
А  =
=  = 8+3= 11
= 8+3= 11
А 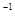 =
= 
Перевірка
А· А 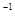 =
= 
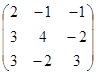 =
= 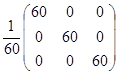 =
= 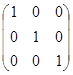 ;
;
X= А 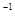 ·b=
·b=  *
* 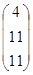 =
=  ;
;
x  =3;
=3;
x  =1;
=1;
x  =1.
=1.
2. Елементи векторної алгебри
Завдання з векторної алгебри спрямовані на засвоєння основних означень векторної алгебри, скалярного, векторного і мішаного добутків.
Вектор – величина  , повністю визначена своїм напрямом і довжиною. Проекції вектора на координатні осі називають його координатами (декартовими):
, повністю визначена своїм напрямом і довжиною. Проекції вектора на координатні осі називають його координатами (декартовими):  =(
=(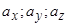 ).
).
Якщо відомі координати початку і кінця вектора 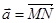 , де M(
, де M( ) та N(
) та N( ), то за формулою
), то за формулою 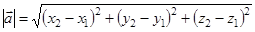 (або
(або  ) можна визначити його модуль (довжину).
) можна визначити його модуль (довжину).
Якщо  - кути, що складає вектор
- кути, що складає вектор  з осями координат, то
з осями координат, то  є напрямними косинусами вектора
є напрямними косинусами вектора  .
.
Тоді  ,
, 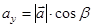 ,
,  і
і  .
.
Орт вектора  позначається
позначається  , а
, а  .
.
Скалярним добутком двох векторів  і
і  називають число, що дорівнює добутку їх модулів на косинус кута між ними:
називають число, що дорівнює добутку їх модулів на косинус кута між ними:
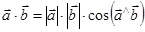 .
.
В координатній формі скалярний добуток має вигляд: 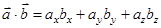 ,
,
тому косинус кута можна знайти за формулою:
 .
.
Властивості скалярного добутку:
1)  (комутативність);
(комутативність);
2)  (дистрибутивність);
(дистрибутивність);
3)  (для будь-якого l);
(для будь-якого l);
4)  .
.
Вектори перпендикулярні, якщо їх скалярний добуток дорівнює нулю. Вектори паралельні, якщо їх координати пропорційні.
Щоб знайти проекцію вектора  на вектор
на вектор  , ми користуємося формулою пр
, ми користуємося формулою пр 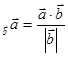 Векторним добутком векторів
Векторним добутком векторів  і
і  називають новий вектор
називають новий вектор 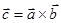 , який визначається трьома умовами:
, який визначається трьома умовами:
|
|
|
1) 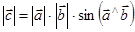 ;
;
2)  перпендикулярний як до
перпендикулярний як до  , так і до
, так і до  ;
;
3) впорядкована трійка векторів  ,
,  та
та  , відкладених від однієї точки, утворює правий базис (правило “буравчика”).
, відкладених від однієї точки, утворює правий базис (правило “буравчика”).
В координатній формі 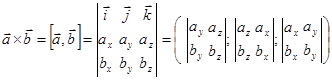 .
.
Властивості векторного добутку:
1)  ;
;
2) 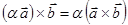 ;
;
3)  ;
;
4)  (якщо
(якщо 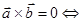 вектори
вектори  та
та  паралельні).
паралельні).
Площу паралелограма, побудованого на векторах  та
та  , обчислюємо за формулою:
, обчислюємо за формулою:
Sпарал.= 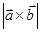 , а площу трикутника можна обчислити за формулою Sтрик.=
, а площу трикутника можна обчислити за формулою Sтрик.=  .
.
Мішаним (скалярно-векторним) добутком трьох ненульових некомпланарних векторів  ,
,  та
та  називають число, абсолютна величина якого дорівнює об’єму паралелепіпеда, побудованого на цих векторах, що виходять з однієї точки.
називають число, абсолютна величина якого дорівнює об’єму паралелепіпеда, побудованого на цих векторах, що виходять з однієї точки.
Це число додатнє, якщо трійка векторів утворює правий базис.
В координатній формі мішаний добуток знаходимо як визначник:  .
.
Властивості мішаного добутку:  ;
;
Якщо вектори  ,
,  та
та  компланарні (тобто належать одній або паралельним площинам), то їх мішаний добуток дорівнює нулю.
компланарні (тобто належать одній або паралельним площинам), то їх мішаний добуток дорівнює нулю.
Якщо вектор  можна представити у вигляді
можна представити у вигляді  , де
, де 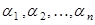 - деякі числа, що одночасно не дорівнюють нулю, то говорять, що вектор
- деякі числа, що одночасно не дорівнюють нулю, то говорять, що вектор  розкладений за векторами
розкладений за векторами  .
.
Теорема. Нехай маємо три некомпланарні вектори  ,
,  та
та  . Будь-який вектор
. Будь-який вектор  може бути єдиним образом розкладений за цими векторами, тобто існують єдині такі числа
може бути єдиним образом розкладений за цими векторами, тобто існують єдині такі числа  , що
, що  .
.
У координатній формі це рівняння перетворюється у систему лінійних рівнянь, де невідомими є числа  .
.
Завдання №1 (варіанти наведені у таблиці 3.3).
Скласти вектори  ;
;  та
та  . Знайти:
. Знайти:
1) модулі векторів  ,
,  та
та  ;
;
2) орти векторів  ,
,  та
та  ;
;
3) кут між векторами  ,
,  і
і  ;
;
4) скалярний добуток 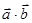 ;
;
5) векторний добуток  ;
;
6) мішаний добуток 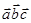 ;
;
7) обчислити вираз 
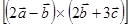 ;
;
8) побудувати на площині вектор  , якщо
, якщо 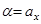 ,
, 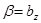 (користуючись правилом паралелограма або трикутника); вектори
(користуючись правилом паралелограма або трикутника); вектори  та
та 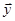 брати довільними;
брати довільними;
9) розкласти вектор 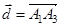 у векторному базисі
у векторному базисі  ,
,  ,
,  (перевірити спочатку, що вектори
(перевірити спочатку, що вектори  ,
,  ,
,  лінійно незалежні).
лінійно незалежні).
|
|
|
3. Аналітична геометрія
Пряма на площині. На площині, де введена прямокутна система координат XOY, розглянемо пряму АВ з заданою точкою М0(x0;y0).
Канонічне рівняння прямої на площині: 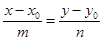 , де
, де  - напрямний вектор прямої, що паралельна прямій АВ.
- напрямний вектор прямої, що паралельна прямій АВ.
|
|
|
|
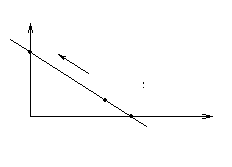 Пряму можна описати і іншими способами:
Пряму можна описати і іншими способами:
|
1) рівняння прямої з кутовим коефіцієнтом
|
 ,
,
де 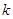 - кутовий коефіцієнт або тангенс додатнього кута, який утворює пряма з додатнім напрямком вісі Ox;
- кутовий коефіцієнт або тангенс додатнього кута, який утворює пряма з додатнім напрямком вісі Ox;
2) рівняння прямої, що проходить через задану точку з заданим кутовим коефіцієнтом
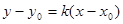 ;
;
3) рівняння прямої, що проходить через дві задані точки:  , де М1(x1;y1) та М2(x2;y2) – відомі точки прямої;
, де М1(x1;y1) та М2(x2;y2) – відомі точки прямої;
4) загальне рівняння прямої:  , де
, де  - нормальний вектор, що направлений перпендикулярно до прямої;
- нормальний вектор, що направлений перпендикулярно до прямої;
5) рівняння прямої у відрізках:  , де
, де  та
та  - відрізки, що відсікає пряма від осей координат;
- відрізки, що відсікає пряма від осей координат;
6) нормальне рівняння прямої:  , де
, де  - перпендикуляр, який опущено на пряму з початку координат, а кут
- перпендикуляр, який опущено на пряму з початку координат, а кут  - це кут між цим перпендикуляром і віссю Ox..
- це кут між цим перпендикуляром і віссю Ox..
Якщо будь-яке загальне рівняння помножити на множник  (знак береться протилежним знаку С), то отримаємо нормоване рівняння прямої.
(знак береться протилежним знаку С), то отримаємо нормоване рівняння прямої.
Відстань від точки М0(x0;y0) до заданої прямої обчислюємо за формулою
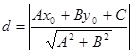 .
.
Координати точки С, яка поділяє пряму АВ на частини, які мають відношення довжин  , обчислюються за формулами
, обчислюються за формулами
 ;
; 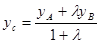 .
.
Паралельність прямих доводиться рівністю їх кутових коефіцієнтів. Перпендикулярність прямих з кутовими коефіцієнтами 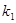 та
та  визначається співвідношенням
визначається співвідношенням  . Кут між прямими можна обчислити за формулою
. Кут між прямими можна обчислити за формулою  . Відстань між двома точками площини обчислюється за формулою
. Відстань між двома точками площини обчислюється за формулою  .
.
Площина. Будь-яка площина у просторі описується лінійним рівнянням
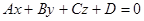 (1)
(1)
і навпаки, будь-яке рівняння (1) у просторі описує деяку площину. Щоб скласти рівняння площини у просторі, достатньо задати точку М0(x0;y0;z0), через яку вона проходить, і вектор  , перпендикулярний площині (нормальний вектор площини). Тоді будь-який вектор
, перпендикулярний площині (нормальний вектор площини). Тоді будь-який вектор 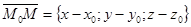 , що належить площині, буде перпендикулярним до
, що належить площині, буде перпендикулярним до  , тобто
, тобто 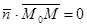 . Це і є векторне рівняння площини.
. Це і є векторне рівняння площини.
У координатній формі маємо 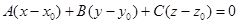 .
.
Щоб скласти рівняння площини, що проходить через три точки М0(x0;y0;z0), М1(x1;y1;z1) та М2(x2;y2;z2), треба виконати умову комплaнарності трьох векторів  ,
,  та
та  , де М(x; y; z) – довільна точка площини, тобто маємо
, де М(x; y; z) – довільна точка площини, тобто маємо  . Мішаний добуток обчислюємо як визначник, складений з координат векторів. Відстань від точки М0(x0;y0;z0) до площини
. Мішаний добуток обчислюємо як визначник, складений з координат векторів. Відстань від точки М0(x0;y0;z0) до площини 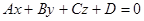 обчислюємо за формулою
обчислюємо за формулою
|
|
|
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 88; Нарушение авторских прав?; Мы поможем в написании вашей работы!