Моделирование работы подвижного состава с использованием марковских случайных процессов

То

Решение

Решение

Решение

Согласно приведенному мнемоническому правилу система диф­ференциальных уравнений Колмогорова имеет вид

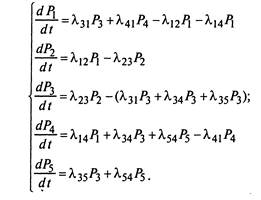
(2.9)

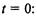
Начальные условия при

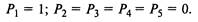
Рассмотрим, что произойдет с системой 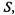описываемой диф­ференциальными уравнениями Колмогорова, при 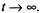Известно, что в случае сообщающихся состояний функции 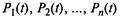стремятся к предельным (финальным) вероятностям состояний си­стемы 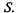Финальные вероятности не зависят от времени. Поэтому в системе дифференциальных уравнений Колмогорова все левые части уравнений (производные) принимают равными нулю. При этом система дифференциальных уравнений превратится в систему линейных алгебраических уравнений.

Для нашего примера система (2.9) будет иметь вид

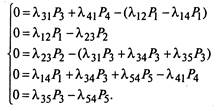
(2.10)

Решая ее с учетом условия 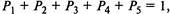получим

все предельные вероятности. Эти вероятности представляют собой не что иное, как среднее относительное время пребывания систе­мы в данном состоянии.

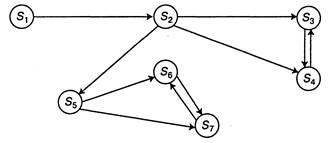
Рис. 2.5. Граф состояний системы S

Состояния S₁, S₂ и S₅ — несущественные, так как из S_{ можно уйти, например, в состояние S₂ и не вернуться, а из состояния S₂ — в состояние S₃ или S₄ и не вернуться, аналогично из состояния S₅ - в состояние S₆ и S₇. Состояния S₃, S₄, S₆ и S₇ — существенные состояния.

Теорема. При конечном числе состоянии для существова­ния финальных вероятностей необходимо и достаточно, чтобы из каждого существенного состояния можно было (за какое-то число шагов) перейти в каждое другое существенное состояние. Граф из примера рис. 2.5 этому условию не удовлетворяет, так как из существенного состояния S₄ нельзя перейти в существенное состояние S₇. Если система S имеет конечное число состояний S₁, S₂,..., S_n, то для существования финальных вероятностей достаточ­но, чтобы из любого состояния системы можно было (за какое-то число шагов) перейти в любое другое состояние.

Если число состояний S₁, S₂,..., S_n бесконечно, то это условие перестает быть достаточным, и существование финальных вероят­ностей зависит не только от графа состояний, но и от интенсивно­сти А,0.

При исследовании непрерывных марковских цепей, как было уже отмечено, часто бывает удобно представить переход системы из состояния в состояние как воздействие каких-то потоков собы­тий (поток заявок на обслуживание, поток автомобилей, поток до­кументов и т. п.). Различают следующие основные свойства, кото­рыми могут обладать случайные потоки событий:

• стационарность;

• ординарность;

• отсутствие последействия.

Свойство стационарности проявляется в том, что вероятность попадания того или иного числа событий на участок времени т за­висит только от длины участка и не зависит от расположения на оси Оt. Другими словами, стационарность означает неизменность вероятностного режима потока событий во времени. Поток, обла­дающий свойством стационарности, называют стационарным. Для стационарного потока среднее число событий, воздействующих на систему в течение единицы времени, остается постоянным. Реаль­ные потоки событий в экономике предприятия являются в дейст­вительности стационарными лишь на ограниченных участках вре­мени.

Свойство ординарности потока присутствует, если вероятность попадания на элементарный участок времени двух и более событий пренебрежимо мала по сравнению с длиной этого участка. Свойст­во ординарности означает, что за малый промежуток времени прак­тически невозможно появление более одного события. Поток, об­ладающий свойством ординарности, называют ординарным. Реаль­ные потоки событий в различных экономических системах либо являются ординарными, либо могут быть достаточно просто приве­дены к ординарным.

Отсутствие последействия — это свойство потока, которое со­стоит в том, что для любых непересекающихся участков времени количество событий, попадающих на один из них, не зависит от того, сколько событий попало на другие участки времени. Поток, обладающий свойством отсутствия последействия, называют пото­ком без последействия. Поток событий, одновременно обладающий свойствами стационарности, ординарности и отсутствия последей­ствия, называется простейшим потоком событий.

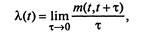
Под интенсивностью потока понимают

(2.11)

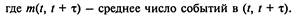
Для простейшего потока интенсивность 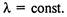Если поток

событий не имеет последействия, ординарен, но не стационарен, то его называют нестационарным пуассоновским потоком, а его ин­тенсивность зависит от времени, т. е.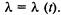

В пуассоновском потоке событий (стационарном и нестацио­нарном) число событий потока, попадающих на любой участок, распределено по закону Пуассона:

(2.12)

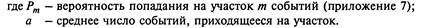
Для простейшего потока 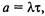а для нестационарного пуассо-

новского потока

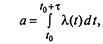
(2.13)

Отметим еще одно важное свойство простейшего потока собы­тий. Промежуток времени t между соседними событиями распреде­лен по показательному закону, а его среднее значение 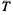и среднее квадратическое отклонение а равны, т. е.

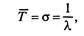
(2.14)

где 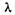— интенсивность потока.

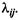
Рассмотрим еще одну типичную схему непрерывных марков­ских цепей, так называемую схему гибели и размножения, часто встречающуюся в разнообразных практических задачах.

Марковский процесс с дискретными состояниями 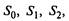..., S_n называется процессом гибели и размножения, если все состоя­ния можно вытянуть в одну цепочку, в которой каждое из средних состояний 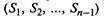может переходить только в соседние со-

стояния, которые, в свою очередь, переходят обратно, а крайние со­стояния 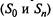переходят только в соседние состояния (рис. 2.6).

Рис. 2.6. Граф состояний для процесса гибели и размножения

Название взято из биологических задач, где состояние популя­ции 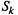означает наличие в ней 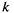единиц особей.

Переход вправо связан с размножением единиц, а влево — с их гибелью.

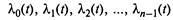— интенсивности размножения, 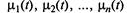— интенсивности гибели.

У X и [I индекс того состояния, из которого стрелка выходит.

С состоянием 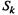связана неслучайная величина 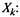если систе­ма 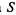в момент времени t находится в состоянии 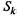, то дискретная случайная величина 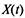, связанная с функционированием систе­мы, принимает значение к. Таким образом, получаем случайный процесс 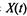, который в случайные, заранее неизвестные моменты времени скачком изменяет свое состояние.

Марковским процессом гибели и размножения с непрерывным вре­менем называется такой случайный процесс, который может при­нимать только целые неотрицательные значения. Изменения этого процесса могут происходить в любой момент времени, т. е. в лю­бой момент времени он может либо увеличиться на единицу, либо уменьшиться на единицу, либо остаться неизменным.

В практике встречаются процессы чистого размножения и чис­той гибели. Процессом чистого размножения называется такой про­цесс гибели и размножения, у которого интенсивности всех пото­ков гибели равны нулю; аналогично процессом чистой гибели называется такой процесс гибели и размножения, у которого ин­тенсивности всех потоков размножения равны нулю.

Пример 2.4. Рассмотрим эксплуатацию моделей автомобилей одной марки в крупной транспортной фирме (на предприятии). Интенсивность поступления автомобилей на предприятие равна 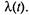Каждый поступивший на предприятие автомобиль списывает­ся через случайное время 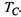Срок службы автомобиля 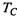распре­делен по показательному закону с параметром 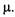Процесс эксплуа­тации автомобилей является случайным процессом. 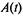— число ав­томобилей данной марки, находящихся в эксплуатации в момент t.

Найдем одномерный закон распределения случайного процесса 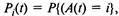если:

1) нет ограничений на число эксплуатируемых машин;

2) на предприятии может эксплуатироваться не более п автомо­билей.

Решение

1. Случайный процесс эксплуатации автомобилей есть процесс гибели и размножения, размеченный граф которого представлен на рис. 2.7.

Рис. 2.7. Граф состояний

Система уравнений Колмогорова, соответствующая этому гра­фу, имеет вид

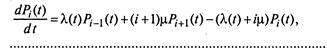
(2.15)

где / = 1, 2,...

Если в начальный момент времени 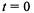на предприятии не бы-

ло ни одного автомобиля, то решать эту систему уравнений нужно при начальных условиях 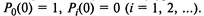Если при

на предприятии было 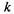автомобилей 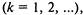то началь-

ные условия будут иметь вид

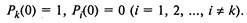
2. Если на предприятии может эксплуатироваться не более п автомобилей моделей одной марки, то имеет место процесс гибели и размножения с ограниченным числом состояний л, размеченный граф которого представлен на рис. 2.8.

Рис. 2.8. Граф состояний

Система уравнений Колмогорова для размеченного графа (рис. 2.8) имеет вид:

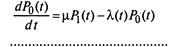
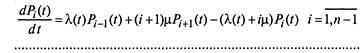
(2.16)

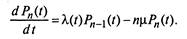
Эту систему надо решать при начальных условиях, рассмотрен­ных выше. Решения систем уравнений (2.15) и (2.16) являются од­номерными законами распределения 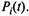Отыскание решений си­стем (2.15) и (2.16) в общем виде при произвольном виде функции

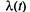представляет значительные трудности и не имеет практических приложений.

При постоянных интенсивностях потоков гибели и размноже­ния и конечном числе состояний будет существовать стационар­ный режим. Система S с конечным числом состояний (п + 1), в ко­торой протекает процесс гибели и размножения с постоянными интенсивностями потоков гибели и размножения, является про­стейшей эргодической системой. Размеченный граф состояний для такой системы представлен на рис. 2.9.

Предельные (финальные) вероятности состояний для простей­шего эргодического процесса гибели и размножения, находящегося в стационарном режиме, определяются по следующим формулам:

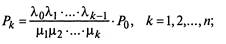
(2.17)

Рис. 2.9. Граф состояний

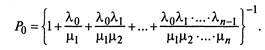
(2.18)

Правило. Вероятность к-го состояния в схеме гибели и размножения равна дроби, в числителе которой стоит произве­дение всех интенсивностей размножения, стоящих левее 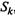, а в знаменателе — произведение всех интенсивностей гибели, сто­ящих левее , умноженной на вероятность крайнего левого со­стояния системы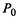

В примере 2.4 для стационарного режима если интенсивность поступления автомобилей постоянная 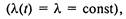то фи-

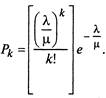
нальные вероятности состояний при условии, что нет ограничений на число автомобилей на предприятии, равны:

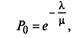
(2.19)

(2.20)

При этом математическое ожидание числа эксплуатируемых ав­томобилей равно его дисперсии:

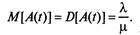
(2.21)

Если существует ограничение по числу автомобилей на пред­приятии (не более n), то финальные вероятности равны

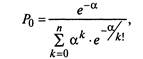
(2.22)

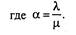
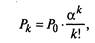
(2.23)

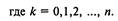
Математическое ожидание числа эксплуатируемых автомоби­лей в стационарном режиме

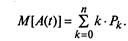
(2.24)

Пример 2.5. В состав ЭВМ входят четыре накопителя на маг­нитных дисках (НМД). Бригада в составе четырех человек обслу­живающего персонала проводит профилактический ремонт каждо­го диска. Суммарный поток моментов окончания ремонтов для всей бригады — пуассоновский с интенсивностью 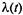. После окон­чания ремонта диск проверяется; с вероятностью Р он оказывает­ся работоспособным (время проверки мало, и им можно прене­бречь по сравнению со временем профилактики). Если диск ока­зался неработоспособным, то вновь проводится его профилактика (время на которую не зависит от того, проводилась ли она ранее) и т.д. В начальный момент все НМД нуждаются в профилактиче­ском ремонте¹.

Требуется:

1) построить граф состояний для системы 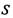(четыре НМД);

2) написать дифференциальные уравнения для вероятностей состояний;

3) найти математическое ожидание числа дисков, успешно прошедших профилактику к моменту ,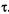

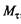
1. Граф состояний показан на рис. 2.10, в котором

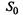— все четыре НМД нуждаются в профилактическом ремонте;

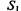— один НМД успешно прошел профилактику, а три НМД нуждаются в профилактическом ремонте;

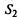— два НМД успешно прошли профилактику, а два нуждают­ся в профилактическом ремонте;

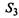— три НМД успешно прошли профилактику, один нуждает­ся в профилактическом ремонте;

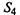— все четыре НМД успешно прошли профилактику.

Рис. 2.10. Граф состояний системы

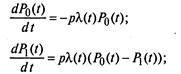
Каждый профилактический ремонт успешно заканчивается с

вероятностью р, что равносильно /^-преобразованию потока окон­чаний ремонтов, после которого он остается пуассоновским, но с интенсивностью pk(f). В этом примере мы имеем дело с процессом чистого размножения с ограниченным числом состояний.

2. Уравнения Колмогорова имеют следующий вид:

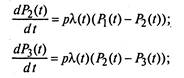
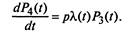(2.25)

Начальные условия 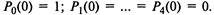При по-

стоянной интенсивности 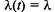и вероятности состояний опреде-

ляются по следующим формулам:

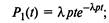
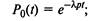
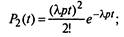
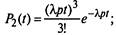
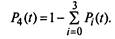
(2.26)

3. Математическое ожидание числа дисков, успешно прошед­ших профилактику к моменту 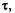равно:

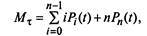
(2.27)

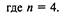
Пример 2.6. Рассмотрим производство автомобилей на заводе. Поток производимых автомобилей — нестационарный пуассонов-ский с интенсивностью 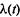. Найдем одномерный закон распределе­ния случайного процесса 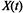— число выпущенных автомобилей к моменту времени t, если в момент 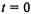начат выпуск автомобилей.

Очевидно, что здесь процесс чистого размножения без ограни­чения на число состояний, при этом 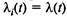, так как интенсив­ность выпуска автомобилей не зависит от того, сколько их уже вы­пущено. Граф состояний такого процесса показан на рис, 2.11.

Рис. 2.11. Граф состояний

Одномерный закон распределения случайного процесса 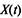для графа, изображенного на рис. 2.11, определяется следующей систе­мой уравнений Колмогорова:

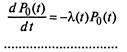
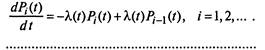
Так как число выпущенных автомобилей 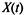на любой фикси­рованный момент / распределено по закону Пуассона с параметром

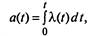
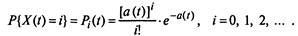
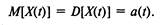
Рассмотренный в этом примере процесс 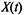называется неодно­родным процессом Пуассона. Если интенсивность 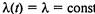:, то

получим однородный процесс Пуассона. Для такого процесса при

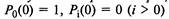
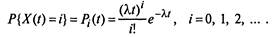
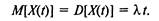
Характеристиками процесса Пуассона будут

Представим автомобиль как некоторую систему 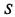с дискретны­ми состояниями 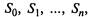которая переходит из состояния в состояние под влиянием случайных событий (отказов).

На стадии прогнозирования (планирования) работы автомоби­ля целесообразно рассматривать следующие состояния, в которых подвижной состав может находиться в процессе эксплуатации и котооые характеризуются целодневными простоями:

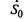— исправен, работает;

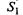— находится на капитальном ремонте (КР);

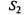— проходит ;

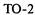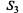— находится в текущем ремонте (ТР);

— исправен, не работает по организационным причинам (без
водителя, шин, запасных частей);

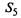— не работает, снятие агрегата для отправки на капитальный
ремонт;

— не работает, списание агрегата, замена на новый;

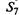— исправен, не работает (выходные и праздничные дни);

— списывается.

Надо отметить, что в настоящее время вышеперечисленные со­стояния автомобиля планируются при разработке годовой програм­мы работы автотранспортного предприятия (АТП), при этом состо­яния 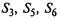объединяются в одно состояние «находится в ТР».

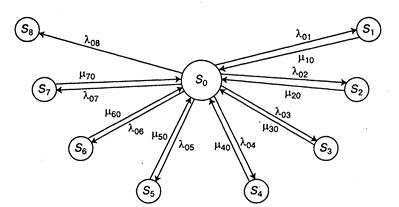
Для анализа процесса эксплуатации автомобиля как случайно­го процесса с дискретными состояниями удобно воспользоваться геометрической схемой, так называемым графом состояний (рис. 2.12). Граф состояний изображает возможные состояния авто­мобиля и его возможные переходы из состояния в состояние.

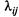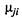На рис. 2.12 через и обозначены плотности вероятнос­тей перехода автомобиля из состояния 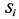в состояние 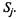Напри-

Рис. 2.12. Граф состояний автомобиля

мер, 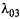— плотность вероятности перехода автомобиля из состо­яния «исправен, работает» в состояние «находится в текущем ре­монте».

Можно считать, что события, переводящие автомобиль из со­стояния в состояние, представляют собой потоки событий (напри­мер, потоки отказов). Если все потоки событий, переводящие сис­тему (автомобиль) из состояния в состояние, пуассоновские (ста­ционарные или нестационарные), то процесс, протекающий в сис­теме, будет марковским, а плотности вероятности перехода 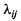в непрерывной цепи Маркова представляют собой интенсивности потока событий, переводящего систему из состояния 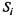в состоя­ние 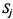. Например, — интенсивность потока отказов автомоби­ля, который переводит автомобиль из состояния «исправен, рабо­тает» в состояние «находится в ТР».

Рассматриваемые состояния автомобиля 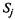характеризуются средним числом дней пребывания автомобиля в каждом состоянии 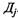. Показатели 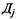находят отражение в статистической отчетно­сти автотранспортного предприятия. Отношение

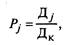
(2.28)

где 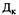— число календарных дней в году.

можно трактовать как вероятность нахождения автомобиля в 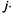-м состоянии.

Вероятности состояний автомобиля 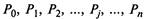как

функции пробега в случае марковского процесса с дискретными состояниями и непрерывным временем удовлетворяют определен­ного вида дифференциальным уравнениям (уравнениям Колмого­рова), записываемым в виде

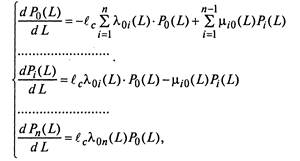
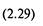
Число уравнений в системе (2.29) зависит от числа состояний автомобиля. Вероятность нахождения автомобиля в состоянии «ис-правен-работает» 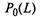представляет собой коэффициент выпуска

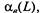а сумма вероятностей 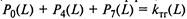- коэф-

фициент технической готовности автомобиля.

Поскольку большинство интенсивностей перехода зависят от пробега, то решение системы (2.29) производится с помощью ме­тодов численного интегрирования, например метода Рунге-Кутта.

Необходимо учесть, что для расчета производственной програм­мы АТП требуется зачастую определять показатели работы группы автомобилей определенной модели у-го возраста (коэффициент вы­пуска и годовой пробег автомобиля у-й возрастной группы).

Для описания процесса функционирования группы автомоби­лей может быть использован метод динамики средних. Этот метод вытекает из теории марковских случайных процессов. Удобство его заключается в том, что, зная возможные состояния одного (услов­ного) автомобиля, можно моделировать процесс функционирова­ния группы из любого числа автомобилей.

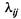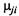Схема, изображающая процесс работы условного автомобиля определенной модели, аналогична схеме рис. 2.12, лишь с той раз­ницей, что через и обозначены средние интенсивности потоков событий, переводящих автомобиль из состояния S; в состояние Sp и наоборот. При этом каждое состояние характеризуется средней численностью автомобилей Nj(t), находящихся в нем в момент вре­мени t. Очевидно, что для любого / сумма численностей всех состо­яний равна общей численности автомобилей исследуемой группы:

Величина 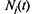для любого / представляет собой случайную ве-

личину, а при меняющемся / — случайную функцию времени.

Зная граф состояний (рис. 2.12) и соответствующие интенсив­ности перехода Х_/7 и jli_/7, определим средние численности автомоби­лей 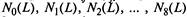как функции пробега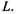

Согласно графу состояний (рис. 2.12) система дифференциаль­ных уравнений для средних численностей состояний запишется следующим образом:

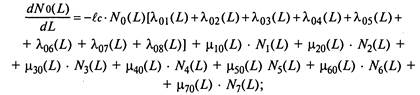
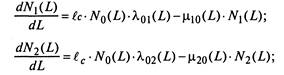
(2.30)

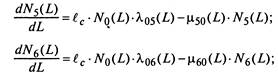
Отношение 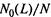равно коэффициенту выпуска автомоби-

лей определенной модели на пробеге L с начала их эксплуатации, а отношение 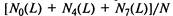— коэффициенту техниче-

ской готовности автомобилей.

Докажем, что формулы для определения коэффициентов техни­ческой готовности (к_тг), выпуска подвижного состава (ос_в) являются частным случаем, соответствующим стационарному решению систе­мы уравнений (2.30), описывающей функционирование автопарка.

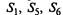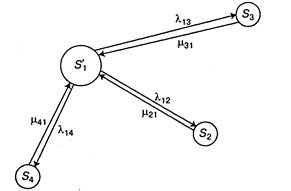
Для расчета средней численности автомобилей, находящихся в исправном состоянии, можно предварительно объединить состояния в одно состояние: «исправен» — 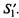Тогда граф состояний условного автомобиля примет вид, представленный на рис. 2.13.

Рис. 2.13. Граф состояний условного автомобиля

Система дифференциальных уравнений для средних численно-стей подвижного состава запишется следующим образом:

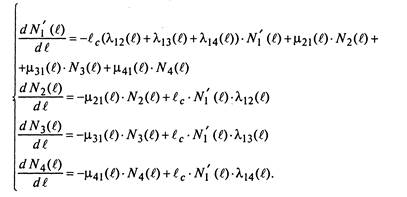
(2.31)

Положим левые части уравнений равными нулю, получим сис­тему алгебраических уравнений для средних численностей состоя­ний автопарка, работающего в стационарном режиме:

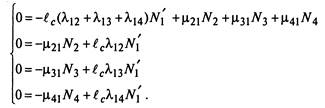
Решим систему алгебраических уравнений с учетом так называ­емого нормировочного условия:

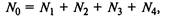
где 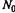, - среднесписочная численность автопарка, шт.

Для примера из системы (2.32) определим неизвестные средние численности состояний, используя N{. Так, из второго и третьего уравнений имеем

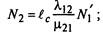
Согласно нормировочному условию

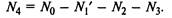
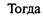
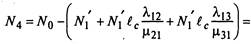
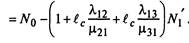
Подставляя в первое уравнение (2.32), получим:

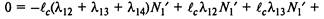
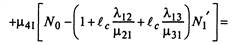
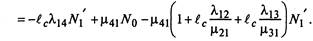
Разделим полученное уравнение на jn^:

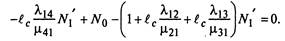
Последнее уравнение можно записать следующим образом:

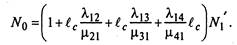
Тогда коэффициент технической готовности равен:

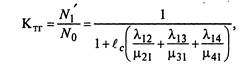
(2.37)

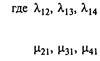
интенсивности перехода автомобиля в состояния «тех­ническое обслуживание», «текущий ремонт», «капиталь­ный ремонт» соответственно, отк/тыс. км; интенсивности восстановления, равные обратным сред­ним величинам продолжительности соответствующих ремонтных воздействий технического обслуживания (ТО-2), текущего ремонта (ТР), капитального ремонта (КР), отк/день.

Дата добавления: 2017-01-14