Решение логических задач табличным способом

Решение.

Пример 5.3

Решение

Пример 5.2

Решение

Пример 5.1

Решение логических задач на основе формул алгебры высказываний

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

ПРИМЕНЕНИЕ АЛГЕБРЫ ЛОГИКИ К РЕШЕНИЮ ЛОГИЧЕСКИХ ЗАДАЧ

Лабораторная работа № 5

ЦЕЛЬ РАБОТЫ – приобретение практических навыков по решению логических задач методами алгебры логики.

Функции алгебры логики широко применяются не только при описании работы дискретных управляющих систем и составлении релейно-контактных схем, но и при решении логических задач. Среди всех способов решения логических задач можно выделить три:

1) на основе формул алгебры высказываний;

2) на основе формул алгебры высказываний с использованием таблиц истинности;

3) табличный.

Покажем на примерах, как использовать возможности данных методов для решения элементарных логических задач.

Суть данного метода заключается в том, что, имея конкретные условия логической задачи, стараются записать их в виде формулы алгебры логики (булевой функции). В дальнейшем путем равносильных преобразований ее упрощают, и простейший вид формулы обычно приводит к ответу на все вопросы задачи. При этом придерживаются следующего порядка.

1. Изучаются условия задачи.

2. Вводится система обозначений для логических высказываний.

3. Конструируется логическая формула, описывающая логические связи между высказываниями, вытекающими из условия задачи.

4. Полученная формула упрощается, и определяются значения истинности логической формулы.

5. Из полученных значений истинности формулы определяются значения истинности введенных логических высказываний, на основании которых делается заключение о решении.

Пытаясь вспомнить победителей прошлогоднего турнира, пять бывших зрителей турнира заявили следующее:

1. Антон был вторым, а Борис – пятым.

2. Виктор был вторым, а Денис – третьим.

3. Григорий был первым, а Борис – третьим.

4. Антон был третьим, а Евгений – шестым.

5. Виктор был третьим, а Евгений – четвертым.

Впоследствии выяснилось, что каждый зритель ошибся в одном из двух своих высказываний. Каково было истинное распределение мест в турнире?

Обозначим высказывания зрителей символом – где , первая буква имени участника турнира, а – номер места, которое он занял в турнире.

Так как в паре высказываний каждого зрителя одно истинно, а второе ложно, то будут истинными дизъюнкции этих высказываний

.

Но тогда будет истинной и формула

.

Упростим формулу, раскрыв скобки и перемножив все члены дизъюнкций между собой.

При этом учтем, что если в полученных конъюнкциях содержатся члены вида , то такая конъюнкция будут ложной (равной нулю), так как одно из высказываний или (пока мы не знаем, какое) обязательно будет ложным, поскольку один человек не может занять одновременно два места, в данном случае второе и третье.

Кроме того, ложными являются и высказывания (конъюнкции) вида , так как не может быть ситуации, когда одно место (в данном случае второе) занимали бы два разных человека.

С учетом вышесказанного, последовательно раскрывая скобки, получим, что функция равна . Ну а конъюнкция истинна (равна 1) тогда и только тогда, когда истинны (равны 1) все ее члены. Отсюда мы получим следующее распределение мест.

Григорий – 1 место, Виктор – 2 место, Антон – 3 место, Евгений – 4 место и Борис – 5 место. На долю Дениса, который не попал в полученную конъюнкцию, но является одним из шести в компании возможных победителей, осталось только 6 место, которое он и занял в действительности.

Жили четыре друга: Александр, Константин, Дмитрий, Федор. И оказалось, что отчества у них были образованы от имен друг друга, таким образом, что у каждого из них имя и отчество не были одинаковы. При этом известно, что отчество Дмитрия не было образовано от Александра, а также то, что имя друга, у которого отчество образовано от имени Федор, соответствует отчеству того друга, имя которого соответствует отчеству Константина.

Определить отчество каждого из друзей.

Обозначим имя и отчество каждого друга символом вида , где - имя (первая буква имени), а 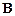- отчество друга (первая буква отчества).

Тогда по условию задачи будут ложны высказывания , так имя и отчество не должны соответствовать друг другу. Ложным, исходя из условия, будет и высказывание , поскольку по условию отчество Дмитрия не образовано от имени Александр, то есть .

Теперь составим высказывания из последнего условия «…имя друга, у которого отчество образовано от имени Федор, соответствует отчеству того друга, имя которого соответствует отчеству Константина». Разберем эту фразу по частям.

«…имя друга, у которого отчество образовано от имени Федор» (обозначим неизвестное имя данного друга через , а его известное, образованное от имени Федор отчество буквой Ф, тогда полностью его обозначение будет ).

Согласно этому же условию имя друга, обозначенного , «…соответствует отчеству того друга…». (Имя «того» друга неизвестно, поэтому обозначим его второй неизвестной переменной , а отчество его соответствует имени друга, обозначенного символом , то есть имеет обозначение , тогда обозначение второго друга будет иметь вид ).

И, наконец, последняя часть фразы, которая говорит о том, что имя друга, обозначенного символом , «…соответствует отчеству Константина». Следовательно, Константина мы должны обозначить символом .

Все полученные по рассмотренному условию высказывания являются истинными, следовательно, будет истинной и конъюнкция

.

Для нахождения отчеств друзей необходимо найти неизвестные и .

Из составленной конъюнкции вытекает, что переменная отвечает условиям . Первое неравенство следует из того, что по условию задачи не могут совпадать имена и отчества, а вторые два из того, что у друзей не может быть одинаковых имен.

Относительно переменной можно записать неравенства . Первое неравенство справедливо, потому что иначе бы одинаковые отчества были у первого и третьего друга, что не разрешено условием. Второе неравенство обусловлено тем, что по условию задачи не могут совпадать имена и отчества.

Таким образом, мы определили два символа и , и остались нерассмотренными еще два – А и Д.

С ними возможны два случая:

1) и ,

2) и .

Но первый случай невозможен, так как из обозначения , заменяя неизвестные переменные приравненными к ним буквами, получим, что , в то время как было установлено, что первое высказывание является истинным, а второе по условию задачи – ложным.

Следовательно, справедлив второй случай и, подставляя в рассмотренную выше конъюнкцию вместо и соответствующие значения, получим , которые определят имена и отчества трех друзей. Для имени четвертого друга осталась только буква , а для его отчества только буква , то есть оставшийся друг будет иметь обозначение . Отсюда друзей звали соответственно: Дмитрий Федорович, Александр Дмитриевич, Константин Александрович и Федор Константинович.

Решение логических задач на основе формул алгебры высказываний с использованием таблиц истинности

Если формула алгебры высказываний не приводит к решению задачи, то для его получения по формуле составляется таблица истинности, которая и позволяет получить искомое решение.

По подозрению в совершенном преступлении задержали Брауна, Джона и Смита. Один из них был уважаемым в городе стариком, другой – малоизвестным чиновником, третий – известным мошенником.

В процессе следствия старик всегда говорил правду, мошенник лгал, а третий задержанный в одном случае говорил правду, а в другом – ложь. При этом они утверждали следующее:

Браун: «Я совершил это. Джон не виноват».

Джон: «Браун не виноват. Преступление совершил Смит».

Смит: «Я не виноват, виновен Браун».

Определить имя старика, мошенника и чиновника. Кто из них виноват, если известно, что преступник один?

Обозначим буквами Б, Д и С соответственно высказывания: «виноват Браун», «виноват Джон», «виноват Смит». Тогда утверждения, высказанные задержанными, можно записать в виде конъюнкций

Браун - ,

Джон - ,

Смит - ,

из которых, по условию задачи, две ложны, а одна истинна.

Для решения этой задачи необходимо составить формулу, а затем по ней составить таблицу истинности.

На основании вышеприведенных конъюнкций составим формулу

,

которая будет истинна, так как одна из конъюнкций истинна.

Из таблицы истинности этой формулы видно, что формула истинна только в пяти из восьми случаев, это – 2, 4, 5, 6 и 7 строки (табл. 4.1). Их мы и рассмотрим.

Обратим внимание на исходные простые высказывания , и . По условию задачи у нас виноват только один человек, поэтому в одной строке под этими высказываниями не могут стоять две единицы, означающие, что виноваты одновременно два человека. Таким образом, необходимо сразу исключить из дальнейшего рассмотрения 4, 6 и 7 строки. Остались 2 и 5.

Таблица 4.1

Таблица истинности формулы

В пятой строке получились истинными две конъюнкции и , что также противоречит условию задачи: истинной является только одна конъюнкция, а значит, этот случай не является справедливым. Следовательно, верным остается случай в строке 2. В ней истинно только одно простое высказывание (под буквой ), и, следовательно, преступником является Смит.

Теперь осталось выяснить, кем являются Браун, Джон и Смит. С этой целью рассмотрим конъюнкции для второй строки. Видим, что истинной является конъюнкция, соответствующая высказыванию , которое принадлежит Джону. Поскольку конъюнкция является истинной только тогда, когда истинны все составляющие ее простые высказывания, то оба высказывания Джона истинны, а следовательно, он является уважаемым в городе стариком, который всегда говорит правду.

Из истинности конъюнкции следует, что , а и , а . Тогда получается, что высказывание Смита составлено из ложных высказываний, и значит, что он всегда лжет, то есть помимо того, что является преступником, он является еще и известным мошенником.

Ну, а на долю Брауна осталась роль малоизвестного и иногда лживого чиновника.

При использовании этого способа условия, которые содержит задача, и результаты рассуждений фиксируются с помощью таблиц.

Дата добавления: 2017-02-01