Лекция 13. Дискретное программирование.

Постановка задачи дискретного программирования. Многиезадачи системного анализа, такие как распределение ресурсов, задачи сетевого планирования и управления, календарного планирования, описываются математическими моделями дискретного программирования.

Рассмотрим общую задачу максимизации.

Найти

при условиях

(13.12)

где D - некоторое множество R⁽ⁿ⁾

Если множество D является конечным или счетным, то условие (13.12) - это условие дискретности, и данная задача является задачей дискретного программирования (ЗДП). Чаще всего условие дискретности разделено по отдельным переменным следующим образом:

где D - конечное (или счетное) множество.

Если вводится ограничение х_; - целые числа (j=l,2,..., n), то приходят к задачам целочисленного программирования (ЦП), которое является частным случаем дискретного программирования.

В задачах дискретного программирования область допустимых решений является невыпуклой и несвязной. Поэтому отыскание решения таких задач сопряжено со значительными трудностями. В частности, невозможно применение стандартных приемов, используемых при замене дискретной задачи ее непрерывным аналогом, состоящих в дальнейшем округлении найденного решения до ближайшего целочисленного. Например, рассмотрим следующую ЗЛП:

найти max (x₁-3x₂ +3х₃) при условиях

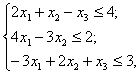
где х₁, х_2, х₃ ≥ 0, x_j - целые числа (j = 1,2, 3). Игнорируя условие целочисленности, находим оптимальный план симплекс-методом:

x_1опт=1/2, x₂⁼0,…,x_2опт= .

Проверка показывает, что никакое округление компонент этого плана не дает допустимого решения, удовлетворяющего ограничениям этой задачи. Искомое целочисленное решение задачи x _1пт =2, x _2опт = 0, x _3опт = 5.

Таким образом, для решения задачи дискретного программирования (ЗДП) необходимы специальные методы. Методы решения ЗДП по принципу подхода к проблеме делят на три группы: 1) методы отсечения или отсекающих плоскостей; 2) метод ветвей и границ; 3) методы случайного поиска и эвристические методы.

Математические модели задач дискретного программирования. По структуре математической модели задачи дискретного программирования разделяют на следующие классы:

1) задачи с неделимостями;

2) экстремальные комбинаторные задачи;

3) задачи на несвязных и на невыпуклых плоскостях;

4) задачи с разрывными целевыми функциями.

Рассмотрим существо некоторых из них.

Задачи с неделимостями. Математические модели задач с неделимостями основаны на требовании целочисленности переменных { x_i}, вытекающем из физических условий практических задач.

К таким задачам относится задача об определении оптимальной структуры производственной программы, где {х_1, х₂,..., х_п} - объемы выпуска продукции.

Эта задача заключается в отыскании

(13.13)

при

(13.14)

(13.15)

Если J =N = (1,2,..., n), то задача называется полностью целочисленной, в противном случае, если J≠N - частично целочисленной.

Задача о ранце. Одной из наиболее распространенных задач целочисленного программирования является так называемая задача о ранце.

Рассмотрим постановку данной задачи. Турист готовится к длительному переходу в горах. В рюкзаке он может нести груз, масса которого не более W. Этот груз может включать в себя п видов предметов, каждый предмет типа j, массой w_j, j = 1,2,..., n. Для каждого вида предмета турист определяет его ценность E_j вовремя перехода. Задача заключается в определении количества предметов каждого типа, которые он должен положить в рюкзак, чтобы суммарная ценность снаряжения была максимальной.

Обозначим через х_j количество предметов j-го типа в рюкзаке.

Тогда математическая модель задачи такова:

(13.16)

при ограничениях

x_j -целое, i= 1,2,..., т. (13.17)

Экстремальные комбинаторные задачи. В данных задачах необходимо найти экстремум некоторой целевой функции, заданной на конечном множестве, элементами которого служат перестановки из nсимволов (объектов).

Одной из наиболее простых задач этого класса является задача о назначениях: найти такую перестановку (р₁,р₂,..., р_n) из чисел 1,2,3,..., n,

при которой обеспечен по всем перестановкам (р₁,р₂,..., р_n). Каждая такая перестановка может быть представлена точкой в п²- мерном евклидовом пространстве или в виде матрицы Х^п

Вводим переменные:

Х_ij = 1, если i -и механизм предназначен для j-й работы; х_ij = 0 — в противном случае.

Очевидно, что должно выполняться условие

(13.18)

Данные ограничения означают, что один механизм может быть предназначен для выполнения только одной работы. Тогда задача будет состоять в определении таких чисел {х_ij}, при которых достигается минимум функционала min 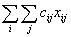при ограничениях (13.18).

Задача о коммивояжере. Имеется (n + 1) город. Задана матрица

С = ||c_ij || расстояний между городами. Выезжая из исходного города A_ij, коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в город А_ij. Требуется определить, в каком порядке следует объезжать города, чтобы суммарное пройденное расстояние было минимально.

Введем переменные:

X_ij — 1, если коммивояжер переезжает из населенного пункта А, в А_j; х_ij - 0 - в противном случае.

Математическая модель задачи имеет следующий вид: найти

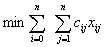(13.19)

при условиях

; (13.20)

; (13.21)

, (13.22)

где u_i, u_j - произвольные целые и неотрицательные числа.

Условие (13.20) означает, что коммивояжер выезжает из каждого города один раз, а условие (13.21)- что он въезжает один раз в каждый город.

Если ограничить задачу только условиями (13.20) и (13.21), она будет эквивалентна задаче о назначениях, план которой не обязан быть цикличным. Иначе говоря, путь коммивояжера при этом можно представить как рад несвязанных подциклов, в то время как его путь в действительности состоит из одного цикла.

Покажем, что для любого цикла, начинающегося в A_ij можно найти u_i удовлетворяющие условию (13.22). Пусть u_i =p, если коммивояжер посещает город А_i на р- мэтапе. Отсюда следует, что

u_i- и_j ≤ п - 1 для всех i и j, и, таким образом, условие (13.22) выполняется при x_ij = 0.

При х_ij = 1 условие (13.22) выполняется как строгое равенство:

u_i-u_j+nx_ij=p-(p+ 1 )+n = n- 1.

Дата добавления: 2017-02-01