
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Короткі теоретичні відомості
|
|
|
|
Методи біостатистики
Конкретні цілі заняття: інтерпретувати типи даних, етапи статистичного аналізу даних, види розподілів, етапи перевірки гіпотез;
демонструвати вміння використовувати статистичні методи обробки медико-біологічних даних.
Основні поняття теми
Параметр, статистична сукупність, випадкова величина, дискретна випадкова величина, неперервна випадкова величина, генеральна сукупність, вибірка (вибіркова сукупність), варіаційний ряд, варіанта, мода, медіана, середнє арифметичне, середнє квадратичне відхилення, помилка репрезентативності, закони розподілу випадкових величин.
1. Основні поняття, методи і формули біостатистики
| Параметр | Властивості, що піддаються оцінці в будь-якій формі (якісній або кількісній) |
| Статистична сукупність | Група, що складається з великої кількості відносно однорідних елементів (об’єктів), узятих разом у певних межах часу або простору |
| Випадкова величина | Величина, яка в результаті експерименту, що може бути повторений за незмінних умов велику кількість разів, може набути значень х1, х2,..., хn .
Види випадкових величин:
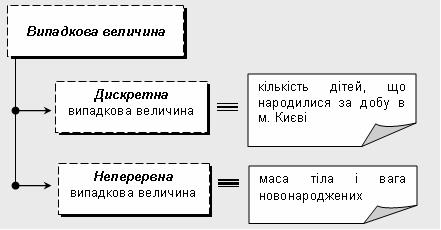
|
| Дискретна випадкова величина | Величина, яка може набувати скінченну кількість значень |
| Неперервна випадкова величина | Величина, яка може набувати будь-яких числових значень у даному інтервалі значень |
| Генеральна сукупність | Сукупність, що складається з усіх одиниць спостереження, що можуть бути до неї віднесені відповідно до мети дослідження |
| Вибірка (вибіркова сукупність) | Частина генеральної сукупності, за властивостями якої судять про генеральну сукупність.
Вимоги до вибіркової сукупності:
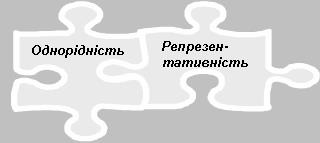
|
| Варіаційний ряд | Сукупність значень вивченого в певному експерименті або спостереженні параметра, проранжованих за величинами (зростання або спадання) |
| Варіанта | Числове значення досліджуваної ознаки; складова варіаційного ряду |
| Середня величина | Узагальнююча числова характеристика якісно однорідних величин, яка характеризує одним числом усю статистичну сукупність за однією ознакою
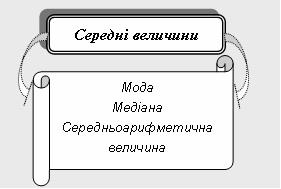
|
| Мода | Значення, найпоширеніше в серії спостережень |
| Медіана | Значення, що поділяє розподіл на дві рівні частини, центральне або середнє значення серії спостережень, упорядкованих за зростанням або спаданням |
| Середньоарифметична величина | Середня величина, яка розраховується за формулою:  (1) (1)
|
| Частота (р) | Абсолютна чисельність окремих варіант у сукупності, що вказує на поширеність цієї варіанти у варіаційному ряду.
Види варіаційного ряду відповідно до значення частоти:
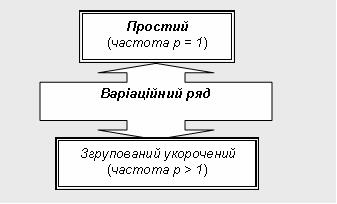
|
| Середнє квадратичне відхилення (s) | Величина, яка характеризує ступінь розсіювання варіаційного ряду навколо середньої величини: 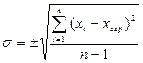 (2) (2)
|
| Коефіцієнт варіації Сv | Величина, необхідна для порівняння ступеня розмаїтості ознак, виражених у різноманітних одиницях виміру. Обраховується за формулою: 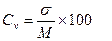 (3) (3)
|
| Помилка репрезентативності | Найважливіша статистична величина, необхідна для оцінки достовірності результатів дослідження: 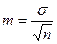 (4) (4)
|
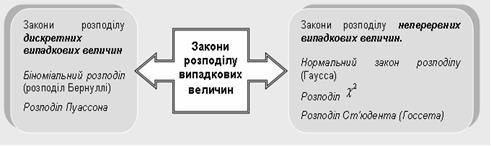
| Закон розподілу випадкових величин | Функціональна залежність між значеннями випадкових величин та ймовірностями, з якими вони набувають цих значень.
Закони розподілу випадкових величин:
|
| Біноміальний розподіл (розподіл Бернуллі) | Дискретна випадкова величина х, яка може набувати тільки цілих невід’ємних значень з імовірностями  m=0, 1,..., n, де р – імовірність появи події в кожному випробуванні, m – кількість сприятливих подій, n – загальна кількість випробувань, q=1–p, m=0, 1,..., n, де р – імовірність появи події в кожному випробуванні, m – кількість сприятливих подій, n – загальна кількість випробувань, q=1–p, 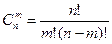 , називається розподіленою за біноміальним законом з математичним сподіванням np та дисперсією npq.
Закон Бернуллі використовують тоді, коли необхідно знайти імовірність появи випадкової події, яка реалізується рівно m з серії n випробувань.
Біноміальному закону розподілу підпорядковуються випадкові події, такі, як кількість викликів швидкої допомоги за певний проміжок часу, черги до лікаря в поліклініці, епідемії тощо , називається розподіленою за біноміальним законом з математичним сподіванням np та дисперсією npq.
Закон Бернуллі використовують тоді, коли необхідно знайти імовірність появи випадкової події, яка реалізується рівно m з серії n випробувань.
Біноміальному закону розподілу підпорядковуються випадкові події, такі, як кількість викликів швидкої допомоги за певний проміжок часу, черги до лікаря в поліклініці, епідемії тощо
|
| Розподіл Пуассона | Дискретна випадкова величина Х, яка може набувати тільки цілих невід’ємних значень з імовірностями
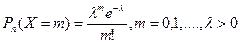 , називається розподіленою за законом Пуассона з математичним сподіванням , називається розподіленою за законом Пуассона з математичним сподіванням 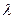 і дисперсією і дисперсією 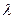 , де , де 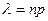 . Розподіл Пуассона як граничний біноміальний використовується при розв’язуванні задач надійності медичного обладнання та апаратури, поширення епідемії, викликів до хворого дільничних лікарів та інших задач масового обслуговування . Розподіл Пуассона як граничний біноміальний використовується при розв’язуванні задач надійності медичного обладнання та апаратури, поширення епідемії, викликів до хворого дільничних лікарів та інших задач масового обслуговування
|
| Нормальний закон розподілу (Гаусса) | У біології та медицині найчастіше розглядають випадкові величини, які мають нормальний закон розподілу: частоту дихання, частоту серцевих скорочень, динаміку росту популяції тощо. Стандартним нормальним розподілом називають розподіл з нульовим математичним сподіванням і одиничною дисперсією, щільність розподілу якого має наступний вигляд:
 
|
Розподіл 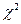
| Нехай незалежні випадкові величини х1, х2,..., хn розподілені за нормальним законом з m c=0 та 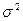 =1. Закон розподілу випадкової величини =1. Закон розподілу випадкової величини  називається «хі-квадрат» розподілом з n ступенями вільності (кількість незалежних координат). Зі збільшенням ступенів вільності розподіл називається «хі-квадрат» розподілом з n ступенями вільності (кількість незалежних координат). Зі збільшенням ступенів вільності розподіл 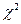 наближається до нормального наближається до нормального
|
| Розподіл Ст’юдента (Госсета) | Нехай х, у – незалежні випадкові величини, причому х розподілено за нормальним законом з параметрами (0;1), у – за законом 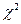 з n ступенями вільності. Тоді розподіл випадкової величини з n ступенями вільності. Тоді розподіл випадкової величини 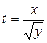 називається законом Ст’юдента з n ступенями вільності або t-розподілом.
При збільшенні ступенів вільності розподіл Ст’юдента наближається до нормального називається законом Ст’юдента з n ступенями вільності або t-розподілом.
При збільшенні ступенів вільності розподіл Ст’юдента наближається до нормального
|
|
|
|
|
|
|
2. Комп’ютерна технологія аналізу результатів
2.1. Оцінка вірогідності результатів прямих вимірювань
Суть цього методу полягає в тому, що за знайденими значеннями Хсер і σ деякої вибірки встановлюють інтервал, у якому з певною імовірністю міститься значення деякого параметра всієї генеральної сукупності.
|
|
|
Імовірність Р, визнана достатньою для певного висновку про досліджуваний параметр генеральної сукупності на основі вибіркових показників, називається надійною.
Вибір того чи іншого значення надійної імовірності здійснюють на основі практичних міркувань і тієї відповідальності, з якою роблять висновки про параметри генеральної сукупності. У медицині при особливо відповідальних експериментах вибирають Рнад=99,9%, у решті випадків – Рнад=95%.
Алгоритм оцінки вірогідності результатів прямих вимірювань.
1. Знаходження за формулою [1] середного арифметичного результатів вимірювання досліджуваної вибірки.
2. Знаходження за формулою [2] середнього квадратичного відхилення окремого результату вимірювання.
3. Знаходження за формулою [4] стандартної похибки.
4. Обчислення точності безпосереднього вимірювання Δm за формулою:
Δm = mtP,ν,
де tP,ν – коефіцієнт нормованих відхилень (коефіцієнт Ст’юдента), залежний від кількості степенів свободи ν=n-1, і вибраної надійної ймовірності (Рнад=99,9%, Рнад=99%, Рнад=95%).
Коефіцієнт Ст’юдента знаходимо за таблицею 1.
| ν | Р | ν | Р | ||||
| 0,95 | 0,99 | 0,999 | 0,95 | 0,99 | 0,999 | ||
| 12,706 | 63,657 | 636,619 | 2,103 | 2,878 | 3,922 | ||
| 4,303 | 9,925 | 31,598 | 2,093 | 2,861 | 3,883 | ||
| 3,182 | 5,841 | 12,941 | 2,086 | 2,845 | 3,850 | ||
| 2,776 | 4,604 | 8,610 | 2,080 | 2,831 | 3,819 | ||
| 2,571 | 4,032 | 6,859 | 2,074 | 2,819 | 3,792 | ||
| 2,447 | 3,707 | 5,959 | 2,069 | 2,807 | 3,767 | ||
| 2,365 | 3,499 | 5,405 | 2,064 | 2,797 | 3,745 | ||
| 2,306 | 3,355 | 5,041 | 2,060 | 2,787 | 3,725 | ||
| 2,262 | 3,250 | 4,781 | 2,056 | 2,779 | 3,707 | ||
| 2,228 | 3,169 | 4,587 | 2,052 | 2,771 | 3,690 | ||
| 2,201 | 3,106 | 4,487 | 2,048 | 2,763 | 3,674 | ||
| 2,179 | 3,055 | 4,318 | 2,045 | 2,756 | 3,659 | ||
| 2,160 | 3,012 | 4,221 | 2,042 | 2,750 | 3,646 | ||
| 2,145 | 2,977 | 4,140 | 2,021 | 2,704 | 3,551 | ||
| 2,131 | 2,947 | 4,073 | 2,000 | 2,660 | 3,460 | ||
| 2,120 | 2,921 | 4,015 | 1,980 | 2,617 | 3,373 | ||
| 2,110 | 2,898 | 3,965 |
5. Знаходження точного значення вимірюваної величини:
Х = Х сер ± Δm.
Цей вираз означає, що шукане значення досліджуваного параметра генеральної сукупності з вибраною надійною імовірністю не виходить за межі інтервалу: Хсер – Δm < Х <Хсер + Δm.
|
|
|
В MS Excel для оцінки вірогідності результатів прямих вимірювань існує вбудована функція ДОВЕРИТ.
2.2. Оцінка вірогідності відмінностей дослідження двох незалежних вибірок
Маємо дві групи вимірювань: дослідну х1, х2,..., хn та контрольну у1, у2,..., уn, де n1 – кількість вимірювань 1-ї групи, n2 – кількість вимірювань 2-ї групи. Використовуючи цей метод, можна встановити, чи спричинені відмінності двох незалежних вибірок випадковим фактором, чи якою-небудь зовнішньою дією (зокрема лікувальною).
Алгоритм оцінки вірогідності відмінностей дослідження двох незалежних вибірок
1. Знаходження середнього арифметичного значення контрольної та дослідної груп.
2. Знаходження середнього квадратичного відхилення окремих вимірювань у групах.
3. Визначення помилок репрезентативності цих груп.
4. Знаходження абсолютного значення середніх арифметичних дослідної та контрольної груп:
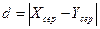 .
.
5. Обчислення середньої похибки різниці.
 .
.
6. Визначення критерію вірогідності різниці:
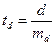 .
.
7. Знаходження кількості ступенів свободи:
ν =n1+n2 - 2.
8. Знаходження за таблицею кількості ступенів свободи ν (див. нижче) значення трьох стандартних критеріїв Ст’юдента (tst), відповідних трьом програмам вірогідності (95%, 99%, 99,9%).
| Кількість ступенів свободи | 95% | 99% | 99,9% | Кількість ступенів свободи | 95% | 99% | 99,9% |
| 12,7 | 63,7 | 637,0 | 2,2 | 3,0 | 4,2 | ||
| 4,3 | 9,9 | 31,6 | 14-15 | 2,1 | 3,0 | 4,1 | |
| 3,2 | 5,8 | 12,9 | 16-17 | 2,1 | 2,9 | 4,0 | |
| 2,8 | 4,6 | 8,6 | 18-20 | 2,1 | 2,8 | 3,9 | |
| 2,6 | 4,0 | 6,9 | 21-24 | 2,1 | 2,8 | 3,8 | |
| 2,4 | 3,7 | 6,0 | 25-28 | 2,1 | 2,8 | 3,7 | |
| 2,3 | 3,5 | 5,4 | 29-30 | 2,1 | 2,7 | 3,7 | |
| 2,3 | 3,4 | 5,0 | 31-34 | 2,0 | 2,7 | 3,7 | |
| 2,3 | 3,3 | 4,8 | 35-42 | 2,0 | 2,7 | 3,6 | |
| 2,2 | 3,2 | 4,6 | 43-62 | 2,0 | 2,7 | 3,5 | |
| 2,2 | 3,1 | 4,4 | 63-175 | 2,0 | 2,6 | 3,4 | |
| 2,2 | 3,1 | 4,3 | 2,2 | 2,6 | 3,3 |
9. Порівняння критерію вірогідності td знайденими значеннями (tst95%, tst99%, tst99,9%).
Якщо td < tst95%, то вибіркова різниця ненадійна, тобто відмінності у вибірках випадкові.
Якщо tst95% ≤ td ≤ tst99%, то вибіркова різниця надійна з імовірністю 95%.
Якщо td ≤ tst99,9%, то вибіркова різниця надійна з імовірністю 99,9%.
Цей алгоритм реалізовано в Пакеті аналізу MS Excel (Сервис/Анализ данных/Двухвыборочный t-тест с одинаковыми дисперсиями – для вибірок з однаковими дисперсіями, та Сервис/Анализ данных/Двухвыборочный t-тест с разными дисперсиями – для вибірок з різними дисперсіями).
2.3. Кореляційний аналіз двох випадкових ознак
Цей метод застосовують для встановлення зв’язку між двома ознаками та з метою визначити його вірогідність. При цьому ми маємо виміри двох ознак:
1-а ознака – х1, х2,..., хn;
2-а ознака – у1, у2,..., уn,.
Треба встановити, чи існує зв’язок між змінними ознак х і у, і якщо існує, то яка його вірогідність.
Алгоритм кореляційного аналізу двох випадкових ознак
1. Знаходження середнього арифметичного значення ознак.
2. Обчислення відхилення кожного значення х від хсер:
 ,
, 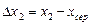 ,...,
,...,  .
.
3. Обчислення відхилення кожного значення у від усер:
 ,
,  ,...,
,..., 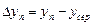 .
.
4. Обчислення суми добутку відхилень:
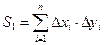 .
.
5. Обчислення максимальної суми:

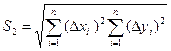 .
.
6. Знаходження коефіцієнта кореляції r:
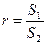 .
.
7. Визначення глибини кореляційного зв’язку за критеріями, навединими нижче:
| êr ê<0,6 | Лінійний взаємозв’язок виявити не вдалося |
| 0,6<êr ê<0,8 | Існує лінійний взаємозв’язок |
| 0,8< êr ê<0,95 | Висока ступінь лінійного взаємозв’язку |
| êr ê>0,95 | Існує практично лінійний зв’язок |
8. Обчислення середньої похибки коефіцієнта кореляції:
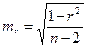 .
.
9. Обчислення критерію вірогідності коефіцієнта кореляції:
 .
.
10. Визначення стандартних значень критеріїв Ст’юдента відповідно трьом програмам вірогідності (95%, 99%, 99,9%) за допомогою таблиці для кількості ступенів свободи (див. вище) ν=2n-2.
11. Порівняння коефіцієнтів вірогідності коефіцієнта кореляції стандартними значеннями критеріїв Ст’юдента. Висновок про вірогідність коефіцієнта кореляції.
В MS Excel для обчислення цього параметру існує вбудована функція КОРРЕЛ.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 149; Нарушение авторских прав?; Мы поможем в написании вашей работы!