
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Марковская модель управления затратами на рекламу
|
|
|
|
Автор: Вилисов Валерий Яковлевич, профессор кафедры Математики Технологического университета (г. Королев, Моск. обл.)
Обратная задача.
Прямая задача.
Игровая модель управления конкурентоспособностью продукции.
Конкурентная среда представлена двумя сторонами:
· 1-й игрок (И1) - это оперирующая сторона, т.е. предприятие, выбирающее оптимальные решения для обеспечения конкурентоспособности продукции (КСП).
· 2-й игрок (И2) – среда, окружающая 1-го игрока, т.е. другие предприятия - конкуренты.
Схема задачи представлена на рисунке.
 |
Здесь 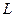 - реакция рынка;
- реакция рынка;  - данные учета по продукту;
- данные учета по продукту;  - объем средств, направляемых на управление конкурентоспособностью продукта;
- объем средств, направляемых на управление конкурентоспособностью продукта;  - решения, принятые для обеспечения конкурентоспособности.
- решения, принятые для обеспечения конкурентоспособности.
КСП характеризуется вектором показателей  . Его состав достаточно стабилен и может быть определен каким-либо из методов практического маркетинга.
. Его состав достаточно стабилен и может быть определен каким-либо из методов практического маркетинга.
Так для теплообменников в  входят технические, экономические и дополнительные показатели (в порядке убывания их значимости):
входят технические, экономические и дополнительные показатели (в порядке убывания их значимости):
· цена;
· надежность (время наработки на отказ);
· срок службы;
· срок поставки;
· гарантийный срок;
· затраты на эксплуатацию;
· затраты на ремонт;
· другие.
Пусть И1 выделяет бюджет  для управления конкурентоспособностью продукта. Пусть рынок находится в равновесии (в установившемся режиме).
для управления конкурентоспособностью продукта. Пусть рынок находится в равновесии (в установившемся режиме).
Необходимо на каждом шаге управления так распределить бюджет  , чтобы обеспечить стабильный спрос.
, чтобы обеспечить стабильный спрос.
Поскольку конкуренты делят общий «пирог» - емкость рынка, то структурно будем рассматривать эту задачу как антагонистическую матричную игру (АМИ) с нулевой суммой. Такая игра однозначно представима своей матрицей платежей 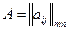 , где
, где 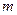 и
и 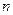 количество чистых стратегий соответственно И1 и И2..
количество чистых стратегий соответственно И1 и И2..
|
|
|
Пусть модель рынка – олигополия.
Чистыми стратегиями АМИ игроков И1 и И2 будем считать элементы расширенного вектора  , в который кроме значимых параметров включен и нулевой элемент, означающий, что из бюджета
, в который кроме значимых параметров включен и нулевой элемент, означающий, что из бюджета  ничего не выделяется на цели управления. Другие элементы вектора
ничего не выделяется на цели управления. Другие элементы вектора  имеют следующий смысл:
имеют следующий смысл:
- элемент «срок поставки», означает, что весь бюджет
 расходуется на снижение срока поставки;
расходуется на снижение срока поставки; - элемент «надежность» означает, что весь бюджет расходуется на повышение надежности работы продукта
· и т.п.
Смешанная стратегия игрока И1 означает распределение бюджета долями для обеспечения соответствующих показателей.
Примем также следующие допущения:
· Множества чистых стратегий игроков И1 и И2 одинаковы, т.к. наборы показателей идентичны у разных участников рынка данного продукта.
· Стороны не знают стратегии, выбираемые на каждом шаге игры, т.е. действуют независимо.
· Поведение игроков разумно.
Поскольку игроки И1 и И2 действуют в условиях неопределенности и антагонизма, то их оптимальными стратегиями будут соответственно максиминная и минимаксная смешанные стратегии 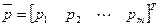 и
и 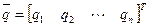 , где
, где 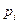 и
и 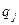 - вероятности применения игроками своих
- вероятности применения игроками своих  - й и
- й и 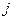 -й стратегий в составе смешанных. Для вероятностей должно выполняться условие нормировки:
-й стратегий в составе смешанных. Для вероятностей должно выполняться условие нормировки:  Кроме того решение АМИ даст и значение цены игры
Кроме того решение АМИ даст и значение цены игры
 (1).
(1).
Если в такой игровой модели все элементы матрицы 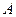 известны, то АМИ можно решить одним из методов (например, сведением АМИ к задаче линейного программирования) и распределить бюджет
известны, то АМИ можно решить одним из методов (например, сведением АМИ к задаче линейного программирования) и распределить бюджет  в соответствии со значениями
в соответствии со значениями 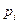 оптимального вектора
оптимального вектора  . Однако обычно матрица
. Однако обычно матрица 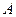 априори не известна. Кроме того прибыль не единственная мера выигрыша, а значит выигрыш носит векторный характер (и должен быть описан набором платежных матриц).
априори не известна. Кроме того прибыль не единственная мера выигрыша, а значит выигрыш носит векторный характер (и должен быть описан набором платежных матриц).
Таким образом, при моделировании рыночной ситуации с помощью АМИ существуют:
|
|
|
- априорная неопределенность – элементы матрицы
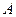 заранее неизвестны;
заранее неизвестны; - текущая неопределенность – в процессе функционирования рынка параметры матрицы
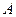 могут изменяться.
могут изменяться.
Для преодоления этих неопределённостей воспользуемся решением обратной задачи – оцениванием элементов матрицы 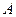 по наблюдениям за решениями, принятыми ЛПР и зарекомендовавшими себя эффективными («хорошими»). Тогда по полученным оценкам матрицы
по наблюдениям за решениями, принятыми ЛПР и зарекомендовавшими себя эффективными («хорошими»). Тогда по полученным оценкам матрицы 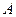 , отражающим обобщенные векторные платежи, можно в новых ситуациях решать и исходную (прямую) АМИ.
, отражающим обобщенные векторные платежи, можно в новых ситуациях решать и исходную (прямую) АМИ.
Пусть в дискретные моменты 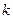 измерены смешанные стратегии игроков
измерены смешанные стратегии игроков  ,
,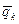 и выигрыш И1
и выигрыш И1  .
.
Построим алгоритм оценивания элементов матрицы 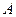 в рекуррентной форме.
в рекуррентной форме.
Уравнение измерений для произвольного (k -го) наблюдения, с учетом (1), примет вид:
 , (2)
, (2)
откуда невязка
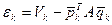 , (3)
, (3)
где  - случайная составляющая (невязка), обусловленная как неточностью измерений, так и степенью соответствия модели игры (матрицы А) реальной ситуации на рынке.
- случайная составляющая (невязка), обусловленная как неточностью измерений, так и степенью соответствия модели игры (матрицы А) реальной ситуации на рынке.
Для оценки элементов матрицы А воспользуемся методом наименьших квадратов (МНК). Согласно МНК критерий оптимальности оценок можно представить в следующем виде:
 , (4)
, (4)
где N – число наблюдений в выборке.
Приведем уравнение (2) к матричной форме. Для этого представим скаляр 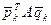 , или, что то же самое,
, или, что то же самое, 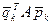 в несколько ином виде - переформируем матрицу А в вектор
в несколько ином виде - переформируем матрицу А в вектор 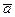 , для чего обозначим:
, для чего обозначим:
 , (5)
, (5)
где вектор 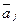 - это
- это 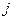 -й столбец матрицы
-й столбец матрицы 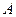 , тогда для всех
, тогда для всех 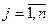 :
:
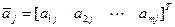 . (6)
. (6)
С учетом этих обозначений выразим 1-е слагаемое в (2):
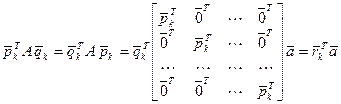 . (7)
. (7)
Здесь
 , (8)
, (8)
где  - i- й компонент вектора
- i- й компонент вектора 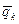 ,
, 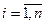 ,
,
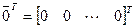 .
.
С учетом этих обозначений выигрыш на k -ом шаге (уравнение измерений (2)) примет вид:
 . (9)
. (9)
Для N шагов эти уравнения можно представить в векторной форме следующим образом:
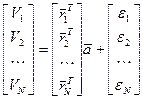 , (10)
, (10)
или, иначе:
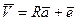 . (11)
. (11)
Отсюда сумму квадратов отклонений (невязок) можно представить в таком виде:
 . (12)
. (12)
Тогда критерий оптимальности оценок, аналогичный (4), но построенный для новой формы ЦФ (12), можно представить в следующем виде:
 , (13)
, (13)
Далее в соответствии с алгоритмом построения МНК-оценок по совокупности N измерений вектор платежей примет вид:
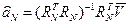 , (14)
, (14)
где нижний индекс отражает количество измерений, по которым выполняется оценивание, а «крышка» над  означает, что вычислена оценка вектора платежей, а не истинные их значения.
означает, что вычислена оценка вектора платежей, а не истинные их значения.
|
|
|
Обозначим:
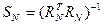 . (15)
. (15)
Представим алгоритм оценивания (14), (15) в рекуррентной форме:
 , (16)
, (16)
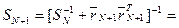
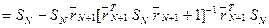 . (17)
. (17)
Алгоритм (16), (17) позволяет ЛПР накапливать положительный опыт принятия решений путем подстройки (уточнения) элементов платежной матрицы по мере появления новых наблюдений. А полученные на основе этой матрицы решения (стратегия  ) путем решения прямой АМИбудут основаны на этом опыте и обеспечат достижения желаемой конкурентоспособности выпускаемой продукции.
) путем решения прямой АМИбудут основаны на этом опыте и обеспечат достижения желаемой конкурентоспособности выпускаемой продукции.
Пример. Рассмотрим случай, когда АМИ размерности m x n = 2х2:

Для нахождения решения прямой АМИ, т.е.  ,
,  и цены игры
и цены игры 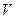 можно свести АМИ к паре задач линейного программирования (ЗЛП) – прямой и двойственной. Тогда прямая задача примет вид:
можно свести АМИ к паре задач линейного программирования (ЗЛП) – прямой и двойственной. Тогда прямая задача примет вид:


Решив эту задачу, получим и решение для И1:

Двойственная задача примет вид:


Решив эту задачу, получим и решение для И2:

Для упрощения расчетов при решении обратной задачи элементы формул (16) и (17) для АМИ 2х2 (индексы номера шага опустим):

Введем обозначения:
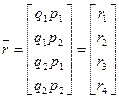 ;
; 
С учетом этого после преобразований формулы (16) по компонентам векторов можно представить в таком виде:
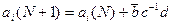
где номер итерации показан в скобках, i - номер компонента вектора;
 , где
, где 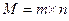


Формулу (17) можно представить в таком виде:
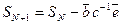
где компоненты вектора  можно представить в таком виде:
можно представить в таком виде:
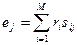 .
.
Приведенные соотношения позволяют вычислить все компоненты векторов и матриц для обратной задачи по текущим измерениям и затем прямой задачи по полученным оценкам матрицы АМИ не только 2х2, но и произвольной размерности.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 508; Нарушение авторских прав?; Мы поможем в написании вашей работы!