Рівняння лінії на площині

Нехай у просторі задано деяку лінію (l) і прямокутну декартову систему координат О xy.

Означення. Рівняння вигляду

F (x,y) = 0 (3.1)

називається рівнянням лінії (l) у заданій системі координат Оху, якщо це рівняння задовольняють координати х і у будь-якої точки, яка належить до лінії (l) і не задовольняють координати жодної точки, яка не належить до цієї лінії.

Таким чином лінія (l) є множиною всіх тих і тільки тих точок площини, чиї координати задовольняють рівняння (3.1). Тому кажуть, що рівняння (3.1) задає (або визначає) лінію (l).

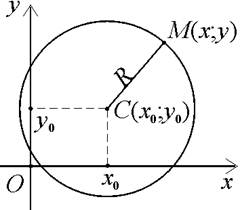
Рис. 3. 1

Якщо лінію задано її геометричними властивостями, то формулюючи аналітично ці властивості, ми одержимо рівняння лінії у вигляді (3.1).

Розглянемо, наприклад, виведення рівняння кола, центр С якого має координати (х ₀; у ₀), а радіус дорівнює R (рис. 3.1). Нехай М (х;у) – будь-яка (як кажуть, поточна) точка кола. Тоді визначальну властивість кола можна записати як . За формулою для відстані між двома точками маємо . Отже, аналітичне формулювання визначальної властивості кола має вигляд

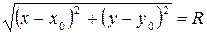, або, підносячи до квадрата,

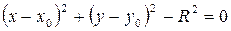. (3.2)

Співвідношення (3.2) задовольняють координати тих і лише тих точок М (х;у),які належать до кола, тобто воно і є рівнянням даного кола. Тут х ₀, у _0, R – сталі числа, які визначають положення і розмір кола, х і у – змінні поточні координати точки кола.

Якщо задано дві лінії з рівняннями відповідно F ₁(x,y) = 0 і F ₂(x,y) = 0, то може постати задача про відшукання точок перетину цих ліній. Точка перетину належить до обох ліній, отже її координати повинні задовольняти рівняння обох ліній. Таким чином геометрична задача відшукання точки перетину двох ліній зводиться до алгебраїчної задачі розв’язання системи рівнянь:

(3.3)

Число розв’язків системи дає число точок перетину ліній.

Приклад. Знайти точки перетину ліній х ² – 2 у – 4 = 0 (парабола 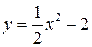) і 2 х – у – b = 0 (пряма). З’ясувати, як залежить число точок перетину від значення параметра b.

Розв’язання: Згідно з попереднім для цього потрібно розв’язати систему рівнянь (3.3) у вигляді:

З другого рівняння у = 2 х + b; якщо підставити це у перше рівняння, одержимо квадратне рівняння відносно х:

х ² – 4 х – 2 b – 4= 0.

Корені цього рівняння і відповідні значення у є координатами точок перетину:

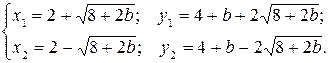(3.4)

Обидві точки перетину суміщаються, якщо підкореневий вираз дорівнює нулю, тобто при b = – 4. При цьому значенні b пряма у = 2 х + b має одну спільну точку з параболою, тобто дотикається до параболи. При 8 + 2 b > 0, тобто b > – 4, точок перетину дві: (х ₁; у ₁) і (х ₂; у ₂). Якщо ж b < – 4, то 8 + 2 b < 0, отже підкореневий вираз у (3.4) від’ємний, і точок перетину не існує.

Означення. Якщо рівняння лінії (l) у деякій системі декартових координат Оху має вигляд

F (x,y) = 0,

де F (x,y) – многочлен степеня n, то кажуть, що (l) – алгебраїчна лінія n-го порядку.

Неалгебраїчні лінії називають трансцендентними.

Дата добавления: 2014-01-04