
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Різні форми рівняння площини
|
|
|
|
Площина як алгебраїчна поверхня першого порядку.
Найбільш загальне рівняння алгебраїчної поверхні першого порядку має вигляд
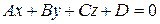 , (3.12)
, (3.12)
де А, В, С, D – числа, при чому хоча б одне з чисел А, В, С, не дорівнює нулю.
|
 Покажемо, що алгебраїчні поверхні першого порядку є площини і тільки площини.
Покажемо, що алгебраїчні поверхні першого порядку є площини і тільки площини.
|
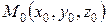 на площині (Р) і який-небудь ненульовий вектор
на площині (Р) і який-небудь ненульовий вектор  , перпендикулярний до площини. Такий вектор називається нормальним вектором площини (Р). Будь-яка точка
, перпендикулярний до площини. Такий вектор називається нормальним вектором площини (Р). Будь-яка точка  лежить на площині (Р) тоді і тільки тоді, коли вектор
лежить на площині (Р) тоді і тільки тоді, коли вектор 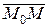 і
і  ортогональні, тобто
ортогональні, тобто 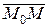 ·
·  = 0. Виражаючи скалярний добуток через координати векторів
= 0. Виражаючи скалярний добуток через координати векторів  і
і 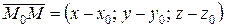 , одержимо рівняння площини (Р) у вигляді
, одержимо рівняння площини (Р) у вигляді
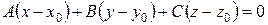 . (3.13)
. (3.13)
Це рівняння називають рівнянням площини за точкою і нормальним вектором.
Розкриємо дужки:

і позначимо 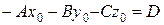 . Одержимо рівняння вигляду (3.12):
. Одержимо рівняння вигляду (3.12):
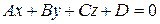 .
.
Таким чином, будь-яка площина є алгебраїчною поверхнею першого порядку, а коефіцієнти А, В, С у рівнянні (3.12) є координатами нормального вектора площини.
В свою чергу легко показати, що будь-яке рівняння (3.12) є рівнянням площини. Нехай 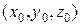 – яка-небудь трійка чисел, що задовольняє рівняння (3.12), тобто
– яка-небудь трійка чисел, що задовольняє рівняння (3.12), тобто  – вірна рівність. Віднімемо почленно цю рівність від (3.12) і одержимо рівняння, еквівалентне (3.13)
– вірна рівність. Віднімемо почленно цю рівність від (3.12) і одержимо рівняння, еквівалентне (3.13)
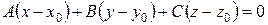 ,
,
тобто рівняння площини, яка проходить через точку  і має нормальний вектор
і має нормальний вектор  . Тому рівняння (3.12) називають загальним рівнянням площини.
. Тому рівняння (3.12) називають загальним рівнянням площини.
 В деяких задачах виникає потреба знайти рівняння площини, яка проходить через три задані точки. Нехай точки
В деяких задачах виникає потреба знайти рівняння площини, яка проходить через три задані точки. Нехай точки  ,
,  і
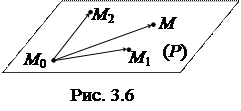
і 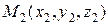 не лежать на одній прямій (рис.3.6). Тоді вектори
не лежать на одній прямій (рис.3.6). Тоді вектори 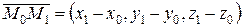 і
і 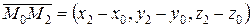 лежать у площині (Р) = (М 0 М 1 М 2) і не колінеарні. Будь-яка точка простору
лежать у площині (Р) = (М 0 М 1 М 2) і не колінеарні. Будь-яка точка простору  належить до площини (Р) тоді і тільки тоді, коли вектори
належить до площини (Р) тоді і тільки тоді, коли вектори  ,
,  ,
,  компланарні. А для компланарності трьох векторів необхідно і достатньо (п.2.8, формула (2.25)), щоб їх мішаний добуток дорівнював нулю:
компланарні. А для компланарності трьох векторів необхідно і достатньо (п.2.8, формула (2.25)), щоб їх мішаний добуток дорівнював нулю:
|
|
|
( ;
; ;
;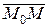 ) = 0.
) = 0.
Визначивши мішаний добуток через координати векторів, одержимо рівняння площини за трьома точками:
 . (3.14)
. (3.14)
Розкриваючи цей визначник за елементами першого рядка, одержимо рівняння площини у формі (3.13).
Приклад 1. Точка  є проекцією точки
є проекцією точки 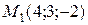 на площину (Р). Написати рівняння цієї площини.
на площину (Р). Написати рівняння цієї площини.
Розв’язання. За умовою задачі точка  лежить на площині (Р), а вектор
лежить на площині (Р), а вектор  перпендикулярний до цієї площини, тобто є нормальним вектором площини (Р):
перпендикулярний до цієї площини, тобто є нормальним вектором площини (Р): 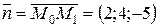 . Значить рівняння площини (Р) можна написати як рівняння площини за точкою і нормальним вектором (3.13):
. Значить рівняння площини (Р) можна написати як рівняння площини за точкою і нормальним вектором (3.13):
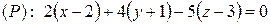 .
.
Розкриваючи дужки, отримуємо:
 .
.
Приклад 2. Знайти площину, яка проходить через точку  і паралельна площині (Р):
і паралельна площині (Р): 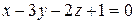 .
.
Розв’язання. Шукана площина (Р 1) проходить через точку  і паралельна до площини (Р 1), значить її нормальний вектор
і паралельна до площини (Р 1), значить її нормальний вектор  колінеарний нормальному вектору
колінеарний нормальному вектору  площини (Р). Можемо взяти
площини (Р). Можемо взяти
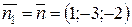 .
.
Тоді рівняння шуканої площини (Р 1) запишеться як рівняння площини за точкою і нормальним вектором (3.13):
 , або
, або
 .
.
Приклад 3. Написати рівняння площини (Р), яка проходить через точку 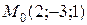 і перпендикулярна до площин
і перпендикулярна до площин

і

Розв’язання. Шукана площина (Р) перпендикулярна до площин (Р 1) і (Р 2), значить її нормальний вектор  повинен бути ортогональним до кожного з нормальних векторів цих площин:
повинен бути ортогональним до кожного з нормальних векторів цих площин: 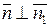 і
і  , де
, де 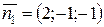 ,
, 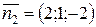 .
.
Цій умові відповідає векторний добуток 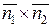 , отже можемо взяти
, отже можемо взяти
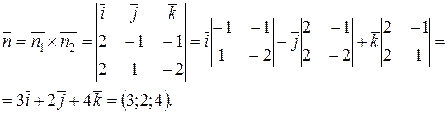
Тоді за формулою (3.13):
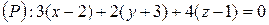 , або
, або
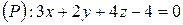 .
.
Приклад 4. Написати рівняння площини (Р), яка проходить через точки  ,
,  ,
, 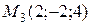 .
.
Розв’язання. Знайдемо рівняння площини (Р) як рівняння площини за трьома точками (3.14):
 .
.
Розкриваємо визначник за елементами першого рядка:

 , або
, або
 .
.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 686; Нарушение авторских прав?; Мы поможем в написании вашей работы!