Індуктивність контура. Явище самоіндукції. Енергія магнітного поля

Нехай по замкненому контуру протікає струм силою І. Індукція магнітного поля, створеного цим струмом, пропорційна до сили струму (, див.§4.2). Величина ж магнітного потоку пропорційна до індукції магнітного поля (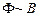, див. §4.6). Отже, магнітний потік через площину контура пропорційний до сили струму в контурі: 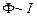або

, (4.41)

де L – коефіцієнт пропорційності між силою струму в контурі і магнітним потоком, що перетинає цей контур, який називається індуктивністю контура. Одиницею вимірювання індуктивності в СІ є генрі:

.

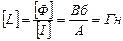Індуктивність контура залежить від його розмірів і форми, а також від магнітної проникливості навколишнього середовища. Як приклад, знайдемо вираз для індуктивності довгого соленоїда – котушки довжиною 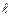і площею поперечного перерізу S, що складається з N витків дроту. При проходженні через соленоїд струму в ньому виникає магнітне поле з індукцією 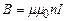, напрямлене вздовж осі соленоїда (див. 4.21). Тоді кожен виток соленоїда перетинає магнітний потік , а повний магнітний потік через соленоїд 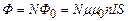. Оскільки 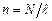– число витків на одиниці довжини соленоїда, то

. (4.42)

Прирівнюючи (4.41) і (4.42), отримаємо для індуктивності соленоїда

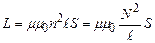, (4.43)

де 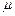– магнітна проникність матеріалу осердя.

Якщо сила струму в контурі змінюється, то змінюється і магнітний потік через контур. Згідно з законом Фарадея (4.40) зміна магнітного потоку викликає появу е.р.с. індукції, яка в даному випадку називається е.р.с. самоіндукції.

Отже, явище самоіндукції полягає у виникненні е.р.с. самоіндукції в контурі, по якому тече змінний електричний струм. Вираз для е.р.с. самоіндукції одержимо, підставивши (4.41) в (4.40):

. (4.44)

Якщо в контурі немає феромагнітних матеріалів, для яких 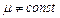, то 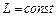і (4.44) спрощується:

, (4.45)

тобто е.р.с. самоіндукції пропорційна до швидкості зміни сили струму в контурі.

Таким чином, в контурі, по якому тече змінний струм, діють дві електрорушійні сили: е.р.с. джерела струму та е.р.с. самоіндукції. Якщо струм в контурі збільшується , то 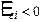. Це означає, що е.р.с. самоіндукції виконує від’ємну роботу, гальмує рух зарядів і тим самим зменшує силу струму в контурі. В даному випадку струм самоіндукції напрямлений проти основного струму. Якщо ж струм в контурі зменшується 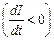, то 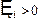робота цієї е.р.с. буде додатньою, а збуджений нею індукційний струм матиме той же напрямок, що і основний струм. Таким чином, і при збільшенні, і при зменшенні сили основного струму е.р.с. самоіндукції протидіє його зміні, тобто тій причині, яка її викликає. В цьому полягає фізичний зміст правила Ленца для явища самоіндукції.

Індукційні струми можуть збуджуватись не тільки в тонких провідниках, які звичайно застосовують в електротехніці, а і в масивних провідниках великих розмірів: барабанах і дисках приладів, осердях котушок тощо. Струми всередині таких суцільних тіл являють собою вихровий рух вільних електронів, тому індукційні струми в масивних тілах (струми Фуко) іноді називають вихровими.

Провідник зі струмом завжди оточений магнітним полем, яке з’являється та зникає разом зі струмом. Очевидно, що енергія магнітного поля дорівнює роботі, виконаній джерелом при створенні цього струму. Розглянемо контур індуктивністю L, по якому тече струм силою І. Його перетинає власний магнітний потік 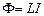. При зміні сили струму на dI магнітний потік змінюється на 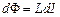. При цьому, згідно з (4.37), джерело струму виконує роботу 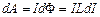. Інтегруючи останній вираз, одержимо 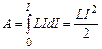. Отже, енергія магнітного поля, створеного струмом контура,

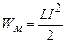. (4.46)

Знайдемо тепер енергію магнітного поля всередині довгого соленоїда. Підставивши (4.43) у (4.46), отримаємо

.

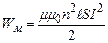Враховуючи, що об’єм магнітного поля практично співпадає з об’ємом соленоїда 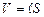, а напруженість магнітного поля в соленоїді 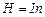, останній вираз запишемо у вигляді

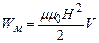. (4.47)

Введемо тепер поняття густини енергії магнітного поля як енергії одиниці об’єму поля

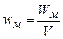. (4.48)

Підставивши (4.47) у (4.48), одержимо вираз для густини енергії магнітного поля

. (4.49)

Цей вираз для густини енергії магнітного поля лишається справедливим для полів, створених провідниками будь-якої форми, а також для полів постійних магнітів.

Дата добавления: 2014-01-04