
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
П Л А Н. 1. Невласні інтеграли з нескінченними межами інтегрування (першого роду)
|
|
|
|
ПЛАН
Завдання додому
Конспект; [1] с. 401-408, 385-393;
[2] с. 299-312.
Питання для самоконтролю
1. Невласні інтеграли з нескінченними межами інтегрування (першого роду).
2. Невласні інтеграли від необмежених функцій (другого роду).
Л Е К Ц І Я 26
Тема: Застосування визначеного інтегралу в економіці.
Мета: розглянути застосування визначеного інтегралу в економіці.
Література: [1, с. 412-420]; [6, с. 408-415].
1. Витрати, доход та прибуток.
2. Коефіцієнт нерівномірного розподілу прибуткового податку.
3. Максимізація прибутку за часом.
4. Дослідження стратегії розвитку.
1. Витрати, доход та прибуток.
Нехай V(x) буде функцією загальних витрат на виробництво x одиниць продукції, V’(x) – функція маргінальних витрат. Тоді визначений інтеграл
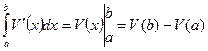 (20)
(20)
дорівнює зміні загальних витрат при зростанні виробленої продукції від a до b одиниць.
Звідси випливає важливий наслідок:
Зміна виробничих витрат при зростанні виробленої продукції від a до b одиниць дорівнює площі криволінійної трапеції, обмеженої графіком функції маргінальних витрат y=V’(x), відрізком [a, b] та прямими x=a та x=b.
Аналогічно, якщо D’(x) та P’(x)- функції маргінального доходу та прибутку, відповідно, то зміни доходу та прибутку при зростанні реалізації виробленої продукції від a до b одиниць обчислюється за формулами
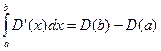 (21)
(21)
 (22)
(22)
Приклад: функція маргінальних витрат фірми має вигляд
V’(x)=23,5-0,01 x
Знайти зростання загальних витрат, коли виробництво зростає з 1000 до 1500 одиниць.
Розв’язування. За формулою (20) зростання загальних витрат буде
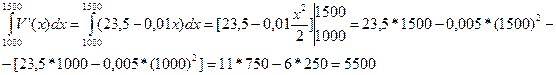
Отже, витрати зростуть на 5500 гривень.
2. Коефіцієнт нерівномірного розподілу прибуткового податку.
Нехай у є частина загального прибуткового податку пропорційна частині x усього населення держави.
|
|
|
Наприклад, якщо x=1/2, а у=1/4, то це означає, що 50% населення сплачує 25% загального прибуткового податку.
Якщо у=0,7, коли x=0,9, то це означає, що 90% населення сплачує 70% прибуткового податку.
У загальному випадку x та у – дробові частини цілого 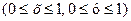 і у є функцією x, тобто у=f(x).
і у є функцією x, тобто у=f(x).
Будемо вважати, що немає осіб, які не сплачують прибуткового податку, тобто f(0)=0 і весь прибутковий податок сплачує 100% населення, тобто f(1)=1.
Графік функції у=f(x), яка описує дійсний розподіл прибуткового податку, називають кривою Лоренцa.
Припустимо, що крива Лоренцa задана рівнянням

Коли x= 0,2, маємо

Це означає, що 20%населення сплачує 5% загального податку.
Коли x= 0,5, маємо

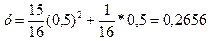
Це означає, що 50% населення сплачує тільки 26,56% податку.
Коефіцієнтом нерівності розподілу податку кривої Лоренцa називають відношення площі фігури, обмеженої кривою Лоренцa та прямою у=х до площі фігури, що лежить нижче прямої у=х.
Коефіцієнт нерівного розподілу податку, що здійснюється за законом Лоренца, позначають L.
Площа трикутника 
Площу заштрихованої фігури одержимо з використанням визначеного інтеграла за формулою
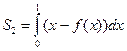
Тому, згідно з означенням, коефіцієнт Лоренца обчислюють за формулою

У випадку кривої Лоренца вигляду

коефіцієнт нерівності розподілу податку буде
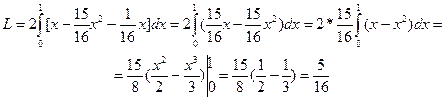
Відмітимо, що коефіцієнт нерівності розподілу податку завжди задовольняє співвідношення 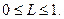
Коли L=0, прибутковий податок розподілено рівномірно, коли L=1, нерівномірність розподілу податків найбільша.
3. Максимізація прибутку за часом.
Нехай V(t), D(t) та P(t)- загальні витрати, доход та прибуток, що змінюються з часом, тобто залежать від часу t. Тоді
P(t)= D(t)- V(t) або
P’(t)= D’(t)- V’(t)
Максимум загального прибутку буде тоді, коли
P’(t)=0 або D’(t)= V’(t)
Іншими словами, існує такий час t1, коли D’(t)= V’(t), тобто швидкості зміни дохода та витрат рівні. Загальний прибуток за час t1 можна знайти за формулою:
|
|
|
 (24)
(24)
Максимум прибутку дорівнює площі між кривими D’(t) та V’(t) на проміжку 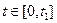 .
.
Приклад. Швидкості зміни витрат та доходу підприємства після початку його діяльності визначилися формулами
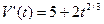 та
та 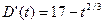
де V та D вимірювались мільйонами гривень, а t вимірювали роками. Визначити, як довго підприємство було прибутковим та знайти загальний прибуток, який було одержано за цей час.
Розв’язування. Оптимальний час t1 для прибутку підприємства одержимо з умови D’(t)= V’(t):
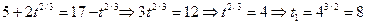
Отже, підприємство було прибутковим 8 років. За цей час було одержано прибутку
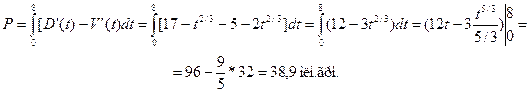
4. Дослідження стратегії розвитку.
Приклад.
Компанія повинна обрати одну із двох можливих стратегій розвитку:
1) вкласти 10 млн. гривень у нове обладнання і одержувати 3 млн. гривень прибутку кожного року на протязі 10 років;
2) закупити на 15 млн. гривень більш досконале обладнання, яке дозволить одержати 5 млн. гривень прибутку щорічно на протязі 7 років.
Яку стратегію треба обрати компанії, якщо номінальна облікова щорічна ставка 10%.
Розв’язування. Якщо f(t) є прибуток за час t i r=R/100 є номінальна облікова щорічна ставка, то дійсне значення загального прибутку за час між t=0 та t=Т дорівнює

При R=10 маємо r=0,1. Тому для першої стратегії дійсне значення прибутку за 10 років буде
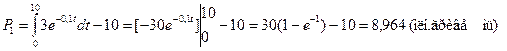
Для другої стратегії одержимо:

Отже, друга стратегія краще першої і тому її доцільно обрати для подальшого розвитку компанії.
Питання для самоконтролю
1. Витрати, доход та прибуток.
2. Коефіцієнт нерівномірного розподілу прибуткового податку.
3. Максимізація прибутку за часом.
4. Дослідження стратегії розвитку.
Л Е К Ц І Я 27
Тема: Диференціальні рівняння. Основні поняття.
Мета: сформувати поняття диференціального рівняння першого порядку; ознайомити з задачею Коші.
Література: [1, с. 421-430]; [6, с. 436-443].
1.Основні означення.
2. Задача Коші.
3. Неповні диференціальні рівняння.
1. Диференціальним рівнянням першого порядку називається рівняння, яке містить незалежну змінну х, невідому функцію у = у (х) та її похідну у’:
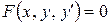 або
або 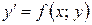
Враховуючи, що 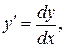 диференціальне рівняння можна записати в диференціалах:
диференціальне рівняння можна записати в диференціалах:
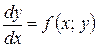
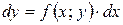
Порядок диференціального рівняння визначається по порядку старшої похідної цього рівняння:
|
|
|
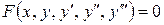 - ІІІ порядку.
- ІІІ порядку.
Розв’язком диференціального рівняння 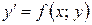 на деякому інтервалі (а; b) називається диференційована на цьому інтервалі функція
на деякому інтервалі (а; b) називається диференційована на цьому інтервалі функція 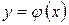 , яка при підстановці в диференціальне рівняння обертає його в тотожність.
, яка при підстановці в диференціальне рівняння обертає його в тотожність.
Графік розв’язку диференціального рівняння називається інтегральною кривою цього рівняння.
2. Теорема Коші (про існування і єдиність розв’язку)
Дано диференціальне рівняння 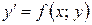 . Нехай функція
. Нехай функція 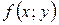 і її частинна похідна
і її частинна похідна  визначені і неперервні в деякій області D і нехай точка
визначені і неперервні в деякій області D і нехай точка 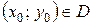 . Тоді існує єдиний розв’язок
. Тоді існує єдиний розв’язок 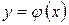 рівняння
рівняння 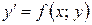 , який задовольняє умову
, який задовольняє умову 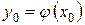 при
при  .
.
Геометрично теорема Коші стверджує, що через кожну точку області D проходить єдина інтегральна крива.
Умову  при
при 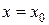 або
або 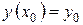 або
або 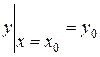 називають початковою умовою розв’язку.
називають початковою умовою розв’язку.
Умови існування і неперервності 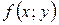 і
і  в області D називають умовами теореми Коші.
в області D називають умовами теореми Коші.
Зауваження: Точки області D, в яких не виконуються умови теореми Коші називаються особливими. Через кожну з таких точок проходить кілька інтегральних кривих або не проходить жодної.
Задача знаходження розв’язку диференціального рівняння 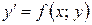 при початкових умовах
при початкових умовах 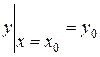 називається задачею Коші.
називається задачею Коші.
Загальним розв’язком рівняння 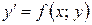 називається функція
називається функція 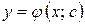 , яка залежить від змінної
, яка залежить від змінної 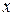 і довільної сталої С.
і довільної сталої С.
Геометрично загальний розв’язок визначає сім’ю інтегральних кривих.

 у
у
 с1
с1

 с2
с2
с=с0
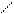
 с1
с1
 |

 0 х
0 х
Частинним розв’язком рівняння 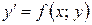 називається функція
називається функція 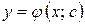 , яка знаходиться із загального розв’язку пр певному значенні сталої с=с0.
, яка знаходиться із загального розв’язку пр певному значенні сталої с=с0.
С0 знаходиться, використовуючи початкові умови.
Геометрично частинний розв’язок визначає одну криву із сім’ї інтегральних кривих, яка проходить через точку 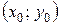 і для якої с=с0.
і для якої с=с0.
Загальний розв’язок називають загальним інтегралом диференціального рівняння.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 344; Нарушение авторских прав?; Мы поможем в написании вашей работы!