
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Площа трикутника
|
|
|
|
План
Тема 3. Вектори
1. Вектори, лінійні операції над векторами.
2. Скалярний, векторний і мішаний добуток векторів.
3. Найпростіші задачі аналітичної геометрії.
1. Вектори, лінійні операції над векторами
Означення. Вектором називається напрямлений відрізок. Позначати вектори будемо 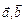 ,.... Якщо, скажімо, точка А — початок вектора, а точка В — його кінець, то маємо
,.... Якщо, скажімо, точка А — початок вектора, а точка В — його кінець, то маємо  .
.
Вектор, в якого початок і кінець збігаються, називається нульовим вектором.
Вектор вважається заданим, коли відома його довжина  ,
,  і напрям щодо деякої осі.
і напрям щодо деякої осі.
Два вектори 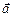 і
і 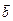 називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих.
називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих.
Вектори 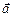 і
і 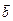 вважаються рівними, коли вони: 1) колінеарні; 2) однаково напрямлені; 3) їхні довжини рівні.
вважаються рівними, коли вони: 1) колінеарні; 2) однаково напрямлені; 3) їхні довжини рівні.
З останнього випливає, що при паралельному перенесенні вектора дістаємо новий вектор, що дорівнює попередньому, тому вектори в аналітичній геометрії називають вільними.
Нехай у просторі задано деяку вісь l і вектор . Проведемо через точки А і В площини, перпендикулярно до осі l (рис. 2.7). Позначимо точки перетину цих площин з віссю l відповідно
. Проведемо через точки А і В площини, перпендикулярно до осі l (рис. 2.7). Позначимо точки перетину цих площин з віссю l відповідно  і
і 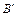 .
.
 Рис. 3.1
Рис. 3.1
|
Означення. Проекцією вектора  на вісь l називається довжина
на вісь l називається довжина 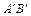 напрямленого відрізка
напрямленого відрізка 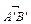 на осі l. Слід зазначити, що
на осі l. Слід зазначити, що  , якщо напрям
, якщо напрям 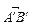 збігається з напрямом l і
збігається з напрямом l і  , якщо напрям
, якщо напрям 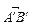 протилежний напряму l.
протилежний напряму l.
Позначається проекція вектора  на вісь l — прl
на вісь l — прl  . З рис. 2.7 випливає формула знаходження проекції вектора на вісь:
. З рис. 2.7 випливає формула знаходження проекції вектора на вісь:
прl  =
=  ,
,
де 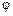 — кут між вектором і віссю.
— кут між вектором і віссю.
Якщо розглянути прямокутну декартову систему координат і точки початку А (х 1, у 1, z 1) і кінця В (х 2, у 2, z 2) вектора  , то проекції вектора
, то проекції вектора  на кожну з осей мають вигляд:
на кожну з осей мають вигляд:
Ох: ах = х 2 – х 1, Оу: ау = у 2 – у 1, Оz: а z = z 2 – z 1.
|
|
|
Довжина вектора подається формулою:
 (3.1)
(3.1)
Якщо позначити a, b, g — кути між вектором  і відповідними осями системи координат, то їх косинуси можна знайти за формулами:
і відповідними осями системи координат, то їх косинуси можна знайти за формулами:
 . (3.2)
. (3.2)
У подальшому називатимемо їх напрямними косинусами вектора 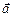 . Піднісши кожну з формул (2.5) до квадрата і скориставшись (2.4), дістанемо:
. Піднісши кожну з формул (2.5) до квадрата і скориставшись (2.4), дістанемо:
cos2a + cos2b + cos2g = 1.
Дії з векторами виконуються за правилами:
1. Додавання:
 = (ах + bх, ау + bу, аz + bz).
= (ах + bх, ау + bу, аz + bz).
2. Множення вектора на число a Î R:
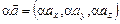 .
.
Для лінійних операцій з векторами виконуються властивості:
1.  .
.
2. 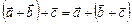 .
.
3. 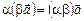 .
.
4. 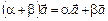 .
.
5.  .
.
Теорема. Проекція суми двох векторів на вісь дорівнює сумі їхніх проекцій на цю вісь:

Теорема. При множенні вектора на число його проекція на цю вісь також множиться на це число:
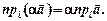
Нехай вектори  такі, що за напрямом збігаються відпо-
такі, що за напрямом збігаються відпо-
відно з осями Ох, Оу, Оz і  . Такі вектори надалі називатимемо одиничними векторами осей системи координат. Тоді
. Такі вектори надалі називатимемо одиничними векторами осей системи координат. Тоді
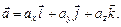 (3.3)
(3.3)
2. Скалярний, векторний і змішаний добуток векторів
Означення. Скалярним добутком двох ненульових векторів  і
і  називається число (скаляр), яке дорівнює добутку модулів цих векторів на косинус кута між ними. Якщо хоча б один із векторів дорівнює нулю, то кут між векторами не визначений і за означенням скалярний добуток дорівнює нулю.
називається число (скаляр), яке дорівнює добутку модулів цих векторів на косинус кута між ними. Якщо хоча б один із векторів дорівнює нулю, то кут між векторами не визначений і за означенням скалярний добуток дорівнює нулю.
Отже:
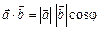 ,
,
де j — кут між векторами. Використовуючи формулу проекції вектора, можна також записати:
 .
.
Властивості скалярного добутку:
1. 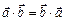 . 4.
. 4.  .
.
2.  . 5.
. 5.  якщо
якщо  і навпаки,
і навпаки,
3. 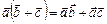 .
.  якщо
якщо 
 .
.
Нехай вектори  і
і  задано за допомогою (2.6), тоді, використовуючи властивості скалярного добутку, умови
задано за допомогою (2.6), тоді, використовуючи властивості скалярного добутку, умови 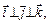 маємо:
маємо:
 (3.4)
(3.4)
Отже, 
З рівності (2.7) випливає, що:
1. Необхідною і достатньою умовою перпендикулярності векторів  і
і  є ах bх + ау bу + аz b z = 0.
є ах bх + ау bу + аz b z = 0.
2. Кут між двома векторами 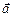 і
і 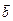 можна знайти за формулою:
можна знайти за формулою:
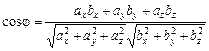 .
.
Означення. Векторним добутком вектора 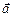 на вектор
на вектор 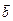 називається вектор
називається вектор 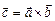 , якщо:
, якщо:
1) довжина вектора  , де j — кут між двома векторами;
, де j — кут між двома векторами;
2) вектор  перпендикулярний до кожного з векторів
перпендикулярний до кожного з векторів 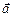 і
і 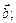
|
|
|
 Рис. 3.2
Рис. 3.2
|
3) вектор  спрямований так, що коли дивитися з його кінця на площину, в якій лежать вектори
спрямований так, що коли дивитися з його кінця на площину, в якій лежать вектори  і
і  , то поворот вектора
, то поворот вектора  до вектора
до вектора  відбувається на найменший кут проти годинникової стрілки.
відбувається на найменший кут проти годинникової стрілки.
Модуль векторного добутку двох неколінеарних векторів дорівнює площі паралелограма, побудованого на векторах як на сторонах.
Властивості векторного добутку:
1.  , якщо
, якщо  і
і  — колінеарні вектори.
— колінеарні вектори.
2.  .
.
3.  .
.
4. 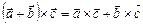 .
.
Знайдемо векторні добутки одиничних векторів  . З колінеарності векторів випливає:
. З колінеарності векторів випливає: 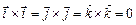 . З того, що одиничні вектори збігаються з напрямом осей прямокутної системи координат, маємо:
. З того, що одиничні вектори збігаються з напрямом осей прямокутної системи координат, маємо:

Знайдемо координати вектора 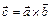 , якщо
, якщо  ,
,  .
.
 (3.5)
(3.5)
або
 .
.
Означення. Мішаним добутком векторів 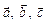 називається число, яке дорівнює скалярному добутку вектора
називається число, яке дорівнює скалярному добутку вектора 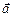 на векторний добуток векторів
на векторний добуток векторів 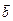 і
і  , тобто
, тобто 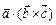 .
.
 Рис. 3.3
Рис. 3.3
|
Розглянемо геометричний зміст змішаного добутку. Для цього побудуємо на векторах  , вважаючи, що вони не лежать в одній площині, тобто не компланарні, паралелепіпед (рис. 2.9).
, вважаючи, що вони не лежать в одній площині, тобто не компланарні, паралелепіпед (рис. 2.9).
Знайдемо об’єм паралелепіпеда, побудованого на векторах 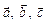 (рис. 2.9). Площа основи його дорівнює модулю векторного добутку векторів
(рис. 2.9). Площа основи його дорівнює модулю векторного добутку векторів 
 . Висота дорівнює
. Висота дорівнює  . Отже, остаточно маємо:
. Отже, остаточно маємо:
 . (3.6)
. (3.6)
З останнього випливає, що модуль мішаного добутку чисельно дорівнює об’єму паралелепіпеда, побудованого на векторах 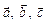 . З рівності (2.9) маємо умову компланарності трьох векторів
. З рівності (2.9) маємо умову компланарності трьох векторів  .
.
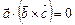 .
.
Ураховуючи формули (2.7) і (2.8) знаходження скалярного і векторного добутків, маємо:

або
 .
.
Властивості мішаного добутку:
1.  .
.
2. 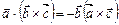 .
.
3. Найпростіші задачі аналітичної геометрії
1. Відстань між двома точками.
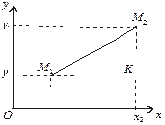 Рис. 3.4
Рис. 3.4
|
Нехай задано дві точки М 1 (х 1, у 1) і
М 2 (х 2, у 2) (рис. 2.10).
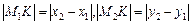 .
.
Трикутник М 1 М 2 K — прямокутний, тому за теоремою Піфагора маємо:
 (3.7)
(3.7)
2. Поділ відрізка у заданому відношенні.
 Рис. 3.5
Рис. 3.5
|
Число l — називається відношенням, в якому точка М ділить відрізок М 1 М 2 (рис. 2.11), якщо
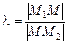 .
.
Нехай задано l і координати точок 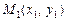 і
і 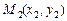 , треба знайти координати точки М (х, у).
, треба знайти координати точки М (х, у).
З рис. 2.11 і теореми про пропорційні відрізки, що відтинають паралельні прямі на сторонах кута, випливають співвідношення:
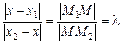 .
.
Оскільки числа х – х 1 і х 2 – х одного й того самого знака (при х 1 < х 2 вони додатні, а при х 1 > х 2 — від’ємні), то  . Отже,
. Отже,  .
.
Звідси:
 . (3.5)
. (3.5)
|
|
|
Аналогічно до попереднього дістанемо формулу для знаходження координати у
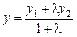 . (3.6)
. (3.6)
Наслідок. Якщо точка М (х, у) — середина відрізка М 1 М 2, то
l = 1 і формули (2.11), (2.12) набирають вигляду:
 .
.
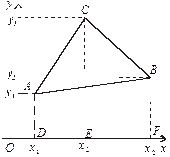 Рис. 2.12
Рис. 2.12
|
Нехай задано координати вершин деякого трикутника А (х 1, у 1), В (х 2, у 2), С (х 3, у 3) (рис. 2.12).
Знайдемо площу цього трикутника.
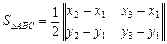
Тема 4. Пряма на площині і в просторі
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 953; Нарушение авторских прав?; Мы поможем в написании вашей работы!