I.Эллиптический параболоид

Параболоиды

Определение 47.4. Эллиптическим параболоидом называется поверхность, координаты всех точек которой в некоторой системе координат удовлетворяют уравнению:

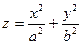(47.24)

Рис 47.10 Рис.47.11 Рис.47.12

Общий вид эллиптического параболоида изображён на рис.47.10, при этом начало координат (для уравнения (47. 24)) будет вершиной параболоида, а ось аппликат OZ (являющаяся его осью симметрии, что легко проверить, ибо если точка 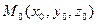лежит на эллиптическом параболоиде, т.е. её координаты 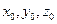удовлетворяют уравнению (47.24), то и координаты симметричной ей относительно оси аппликат точки 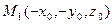также удовлетворяют уравнению (47.24), т.е. эта симметричная точка также находится на эллиптическом параболоиде) является осью эллиптического параболоида.

Эллиптический (точнее - круговой) параболоид вращения получится, если мы параболу будем вращать вокруг её оси симметрии (см.рис. 47.11)

В сечении эллиптического параболоида плоскостями могут получиться:

-парабола (если секущая плоскость параллельна оси параболоида или проходит через неё; исходя из рис.47.12 читателю предлагаем самостоятельно доказать, что в сечении эллиптического параболоида такой плоскостью будет некоторая неограниченная непрерывная кривая второго порядка, т.е. парабола);

-эллипс (когда секущая плоскость не параллельна его оси, пересекает, но не касается эллиптического параболоида; читателю предлагает показать самостоятельно, исходя из рис. 47.12, что в этом случае в сечении возникает некоторая ограниченная кривая второго порядка, т.е. эллипс);

- одна точка (если плоскость касается эллиптического параболоида);

- пустое множество (когда плоскость не пересекает эллиптический параболоид).

Остальные линии в сечении эллиптического параболоида плоскостями получить нельзя.

Дата добавления: 2014-01-04