Частные производные высших порядков. Экстемум функции двух переменных

Лекция 17.

ПЛАН

8. Введение.

9. Частные производные высших порядков.

10. Экстремумы функции двух переменных.

11. Наибольшее и наименьшее значение функции в замкнутой области.

12. Подбор параметров для эмпирических формул простейшего вида по методу наименьших квадратов

13. Заключение.

17.1. Введение

При изучении функции одной переменной кроме производной первого порядка, характеризующей скорость изменения какого-либо процесса, мы ввели понятие второй производной, которая отвечала за ускорение. У функции двух переменных существует две частные производные, которые в общем случае также являются функциями тех же переменных, и, следовательно, их снова можно дифференцировать и по х, и по у. Покажем, как это делается.

17.2. Частные производные высших порядков

Пусть функция z = f (x,y) непрерывна вместе со своими частными производными и в некоторой области D плоскости ХОY.

Определение 17.1. Частными производными второго порядка (или вторыми частными производными) называются производные от производных 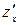и .

Вторые частные производные обозначаются так:

,

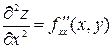здесь функция последовательно дифференцируется по х дважды;

,

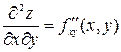здесь f дифференцируется сначала по х, а потом результат по у;

,

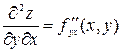здесь f дифференцируется сначала по у, а потом результат по х;

,

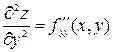здесь f дифференцируется дважды по у.

Первая и последняя производные называются иногда чистыми, а вторая и третья – смешанными производными второго порядка.

Можно доказать (см. учебник Кремера)), что

,

при условии непрерывности этих производных в заданных точках, т. е. вторая смешанная производная не зависит от порядка дифференцирования и поэтому четыре частных производных сводятся к трем.

Производные второго порядка можно вновь дифференцировать как по х, так и по у. Получим производные третьего порядка, две из которых чистые, а остальные шесть – смешанные:

, , , .

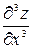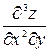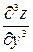Здесь мы учли, что

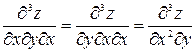и ,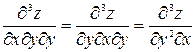

и поэтому восемь частных производных сводятся к четырем.

Этот процесс можно продолжить и получить производные любого порядка, при условии, что все они непрерывны в заданной точке.

Пример 17.1. Вычислить производные второго порядка от функции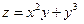

Решение. Найдем производные первого порядка, учитывая, что частная производная по х вычисляется в предположении, что у – постоянная и наоборот:

, .

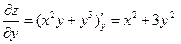Найдем производные второго порядка:

, , , .

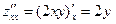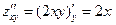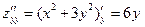Пример 17.2. Дана функция 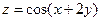. Показать, что .

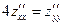Решение. Найдем последовательно значения всех производных и проверим данное равенство.

, , , .

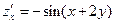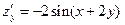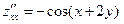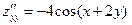Подставим найденные значения в исходное равенство:

.

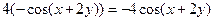Мы видим, что равенство 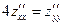для заданной функции выполняется.

Пример 17.3. Дана функция . Показать, что .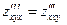

Решение.

, ,

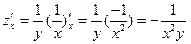– это левая часть равенства.

Для вычисления правой учтем, что 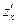уже известно, и найдем

, .

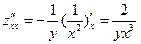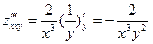Т.о. исходное равенство для заданной функции.

Как видно из приведенных примеров, следует соблюдать бдительность и отделять по возможности те переменные, которые в данном случае играют роль постоянной.

17.3. Экстремумы функции двух переменных

Мы достаточно подробно обсуждали экстремумы функции одной переменной. Перенесем эти знания на функции двух переменных.

Определение 17.2. Точка называется точкой максимума функции 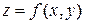, если

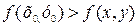
для всех точек (х, у), достаточно близких к точке 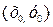и отличных от нее (рис. 17.1).

Определение 17.2. Точка называется точкой минимума функции 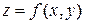, если

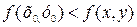
для всех точек (х,у), достаточно близких к точке 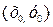и отличных от нее. (рис. 17.2).

Точки, в которых частные производные равны нулю или не существуют, называются критическими.

Иногда точку экстремума и ее характер можно определить из соображений здравого смысла.

Например, функция 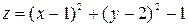имеет минимум пр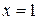и и 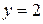, т.е. в точке М (1,2). Действительно, для любых 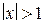первое слагаемое будет расти, и для – тоже, поэтому в точке М (1,2) функция имеет минимум, причем (рис. 17.1).

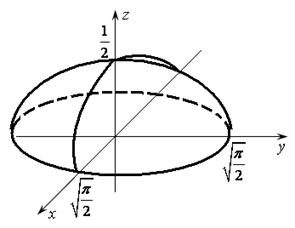
Рис. 17.1 Рис. 17.2

Функция 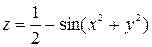имеет максимум в точке (0,0), причем 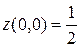(рис. 17.2).

Кроме того, существуют такие точки, где функция по одной переменной имеет минимум, а по другой переменной – максимум. Их называют точками минимакса (рис. 17.3), или седловыми, точками. Они особенно интересны экономистам, если в качестве определяющих переменных служат затраты Х (ден.ед) и прибыль Y (ден.ед.). Ясно, что нужно искать такие точки, в которых затраты были бы минимальными, а прибыль – максимальной.

Рис. 17.3

Но чаще всего определить экстремальную точку бывает затруднительно, поэтому, как и для функции одной переменной введем необходимый и достаточный признаки, позволяющие определять координаты и характер экстремума, не производя лишних вычислений.

Теорема 17.1 (необходимое условие экстремума). Если функция 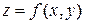достигает экстремума при 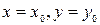, то каждая частная производная первого порядка в этой точке либо равна нулю, либо не существует.

Для достаточного признака существования экстремума введем дополнительные обозначения:

, , ,

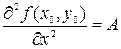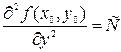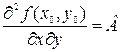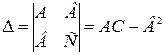. (17.1)

Теорема 17.2. Пусть функция 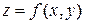имеет непрерывные частные производные до второго порядка включительно, и точка 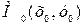является критической, т.е. 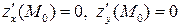. Тогда в этой точке:

1. 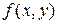имеет максимум, есл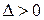и и ;

2. 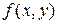имеет минимум, есл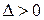и и ;

3. 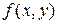не имеет ни максимума ни минимума, если . Возможен минимакс;

4. если , то нужны дополнительные исследования.

Доказательство этих теорем выходит за рамки нашего курса. Его можно найти в рекомендуемой литературе.

Оба признака регламентируют порядок действия для отыскания экстремальных точек.

1. Находим частные производные первого порядка и из системы уравнений:

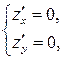
находим координаты критических точек.

2. Находим частные производные второго порядка и их значения в критических точках.

3. Составляем определитель 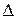по формуле 17.1 и делаем вывод о характере экстремума.

4. Находим аппликату экстремальной точки.

Пример 17.4. Исследовать на максимум и минимум функцию

.

Решение. Следуем по плану.

1. Находим частные производные и приравниваем их к нулю:

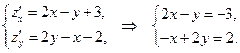
Решая систему уравнений, находим , .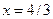

2. Находим частные производные второго порядка:

, , .

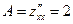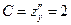3. Составляем определитель

.

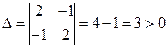Следовательно, функция в точке (4/3,1/3) имеет минимум, т.к. .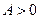

4. .

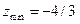Таким образом, точка минимума имеет координаты (4/3, 1/3, –4/3).

Пример 17.5. Исследовать на максимум и минимум функцию

.

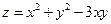Дата добавления: 2014-01-04