
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сжатие данных с помощью сингулярного разложения матрицы
|
|
|
|
Задача наименьших квадратов. Решение линейной задачи наименьших квадратов с помощью сингулярного разложения матрицы
Вырожденные задачи наименьших квадратов
Сжатие данных с помощью сингулярного разложения матрицы
Задача наименьших квадратов. Решение линейной задачи наименьших квадратов с помощью сингулярного разложения матрицы
План
Лекция 30.Использование сингулярного разложения матрицы для решения различных задач
Питання
1. Який ряд називається рядом з додатними членами?
2. Критерій збіжності рядів з додатними членами.
3. Перша ознака порівняння збіжності рядів в формі нерівностей.
4. Перша ознака порівняння в граничній формі.
5. Друга ознака збіжності рядів з додатними членами.
6. Ознаки Коші та Даламбера збіжності рядів з додатними членами в формі нерівностей і в граничній формі.
7. Визначення невластивого інтеграла І роду.
8. Інтегральна ознака Коші-Маклорена збіжності рядів з додатними членами.
Пусть даны 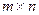 -матрица
-матрица  и
и  -вектор
-вектор 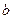 . Линейная задача наименьших квадратов заключается в отыскании
. Линейная задача наименьших квадратов заключается в отыскании 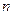 -вектора
-вектора 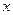 , минимизирующего величину
, минимизирующего величину 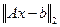 (евклидова норма вектора
(евклидова норма вектора  ). Если
). Если 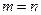 и матрица
и матрица  невырожденная, то решением задачи является вектор
невырожденная, то решением задачи является вектор  (т.е. решение СЛАУ
(т.е. решение СЛАУ 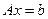 ). Если
). Если  , т.е. число уравнений больше числа неизвестных, то задача называется переопределенной; в этом случае, ввобще говоря, не существует вектора
, т.е. число уравнений больше числа неизвестных, то задача называется переопределенной; в этом случае, ввобще говоря, не существует вектора 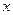 , точно удовлетворяющего системе
, точно удовлетворяющего системе 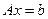 . Иногда встречаются и недоопределенные задачи, где
. Иногда встречаются и недоопределенные задачи, где  .
.
Пример. Аппроксимация данных является традиционным приложением метода наименьших квадратов. Пусть даны  пар чисел
пар чисел  . Предположим, что мы хотим найти кубический полином, который бы «наилучшим образом» представлял числа
. Предположим, что мы хотим найти кубический полином, который бы «наилучшим образом» представлял числа 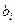 как функцию от
как функцию от 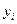 . Это означает, что коэффициенты многочлена третьей степени
. Это означает, что коэффициенты многочлена третьей степени  , нужно определить так, чтобы многочлен
, нужно определить так, чтобы многочлен
|
|
|

минимизировал невязку 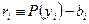 для
для 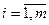 , т.е. перед нами стоит задача минимизации вектора
, т.е. перед нами стоит задача минимизации вектора
 ,
,
где  и
и 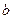 - векторы длины
- векторы длины  ,
,  - матрица размера
- матрица размера  , а
, а  - вектор длины 4. Для минимизации
- вектор длины 4. Для минимизации  можно выбрать любую норму, например,
можно выбрать любую норму, например,  ,
,  или
или  . В последнем случае получаем задачу наименьших квадратов, она соответствует минимизации сумм квадратов невязок:
. В последнем случае получаем задачу наименьших квадратов, она соответствует минимизации сумм квадратов невязок: 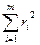 .
.
Пример. В статистическом моделировании часто приходится оценивать некоторые параметры  , основываясь на наблюдениях, «загрязненных» шумом. Предположим, например, что в рамках компании по приему в университет желательно предсказать средний бал
, основываясь на наблюдениях, «загрязненных» шумом. Предположим, например, что в рамках компании по приему в университет желательно предсказать средний бал 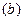 будущего обучения в нем, исходя из среднего бала
будущего обучения в нем, исходя из среднего бала  , который абитуриент имел в старших классах школы, и результатов двух экзаменов (тестов): устного
, который абитуриент имел в старших классах школы, и результатов двух экзаменов (тестов): устного  и письменного
и письменного  . Основываясь на прошлых данных для ранее принятых студентов, можно построить линейную модель вида
. Основываясь на прошлых данных для ранее принятых студентов, можно построить линейную модель вида
 .
.
Наблюдениями являются четверки чисел  ,
,  ,
, 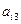 и
и 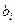 , по одной для каждого из
, по одной для каждого из  студентов в базе данных. Итак, желательно минимизировать величину
студентов в базе данных. Итак, желательно минимизировать величину
 ,
,
что можно рассматривать как задачу наименьших квадратов.
Рассмотрим решение задачи наименьших квадратов при помощи сингулярного разложения матрицы.
Напомним, что спектральная матричная норма матрицы  опрелеляется следующим образом:
опрелеляется следующим образом:
 ,
,
где символ 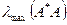 обозначает максимольное собственное значение матрицы
обозначает максимольное собственное значение матрицы  . Если матрица
. Если матрица  - вещественная симметричная, то
- вещественная симметричная, то  , и тогда
, и тогда
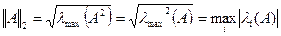 .
.
Утверждение 1. Для спектральной матричной нормы верно равенство
 , (1)
, (1)
где 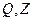 - любые ортогональные матрицы.
- любые ортогональные матрицы.
Можно показать, что если  - невырожденная
- невырожденная  матрица с сингулярным разложением
матрица с сингулярным разложением  , то решением задачи минимизации
, то решением задачи минимизации 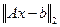 является вектор
является вектор
 .
.
Действительно:
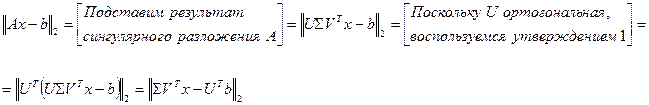
Обозначим в последнем выражении:  , тогда получим:
, тогда получим:
|
|
|
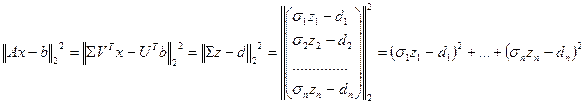 .
.
Минимальное значение  , а значит и
, а значит и  достигает тогда, когда все неотрицательные слагаемые в правой части последнего равенства равны 0:
достигает тогда, когда все неотрицательные слагаемые в правой части последнего равенства равны 0:
 (2)
(2)
Поскольку  - невырожденная матрица, у нее нет нулевых сингулярных чисел, это значит, что мы можем однозначно определить из (2)
- невырожденная матрица, у нее нет нулевых сингулярных чисел, это значит, что мы можем однозначно определить из (2)  :
:
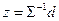 . (3)
. (3)
Подставим в (3) выражения  , получим:
, получим:
 ,
,
откуда  , что и требовалось доказать.
, что и требовалось доказать.
Пусть для матрицы  имеется сингулярное разложение
имеется сингулярное разложение  .
.
Теорема. Если  , где
, где  , - столбцы матрицы
, - столбцы матрицы 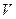 , а
, а  , где
, где 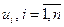 , - столбцы матрицы
, - столбцы матрицы 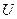 , сингулярное разложение матрицы
, сингулярное разложение матрицы  можно представить в форме внешних произведений:
можно представить в форме внешних произведений:
 ,
,
т.е. в виде суммы матриц  , ранга 1. Тогда ближайшая к
, ранга 1. Тогда ближайшая к  (в смысле спектральной матричной нормы
(в смысле спектральной матричной нормы  ) матрицей ранга
) матрицей ранга 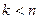 является матрица
является матрица
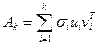 ,
,
называемая малоранговой аппроксимацией матрицы  (или аппроксимацией матрицы
(или аппроксимацией матрицы  ранга
ранга  ), причем
), причем
 .
.
Для матрицы  справедливо также представление
справедливо также представление
 ,
,
где  .
.
Приведенная теорема используется для сжатия изображений. Изображение размера  - это попросту
- это попросту  матрица, элемент
матрица, элемент  которой интерпретируется как яркость точки (пикселя)
которой интерпретируется как яркость точки (пикселя)  . Другими словами, элементы матрицы, изменяющиеся от 0 до 255, интерпретируются как точки с окраской от черной (что соответствует 0) до белой (что соответствует 255) с различными промежуточными степенями серого цвета (возможны и цветные изображения, тогда там будут фигурировать 3 матрицы). Вместо того, чтобы хранить или передавать все
. Другими словами, элементы матрицы, изменяющиеся от 0 до 255, интерпретируются как точки с окраской от черной (что соответствует 0) до белой (что соответствует 255) с различными промежуточными степенями серого цвета (возможны и цветные изображения, тогда там будут фигурировать 3 матрицы). Вместо того, чтобы хранить или передавать все  элементов матрицы, представляющей изображение, часто бывает предпочтительным сжатие этого изображения, т.е. хранение гораздо меньшего массива чисел, с помощью которых исходный образ все же может быть приближенно восстановлен. Проиллюстрируем это на примере изображения размером
элементов матрицы, представляющей изображение, часто бывает предпочтительным сжатие этого изображения, т.е. хранение гораздо меньшего массива чисел, с помощью которых исходный образ все же может быть приближенно восстановлен. Проиллюстрируем это на примере изображения размером  (рис.1), матрицу которого обозначим
(рис.1), матрицу которого обозначим  . При построении сингулярного разложения матрицы
. При построении сингулярного разложения матрицы  этого изображения будет вычислено 480 СНЧ. Согласно предыдущей теоремы матрица
этого изображения будет вычислено 480 СНЧ. Согласно предыдущей теоремы матрица 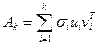 есть наилучшее приближение ранга
есть наилучшее приближение ранга  матрицы
матрицы  в том смысле, что она реализует минимум
в том смысле, что она реализует минимум  величины
величины  . Заметим, что для восстановления матрицы
. Заметим, что для восстановления матрицы  требуется лишь
требуется лишь 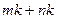 слов памяти, в которых хранятся
слов памяти, в которых хранятся  векторов
векторов 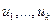 длины
длины  и
и  векторов
векторов 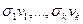 длины
длины 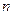 . В то же время дляхранения
. В то же время дляхранения  (или той же матрицы
(или той же матрицы  , но в явном виде) нужны
, но в явном виде) нужны  слов, т.е. гораздо большая память при малом
слов, т.е. гораздо большая память при малом  . Будем рассматривать
. Будем рассматривать  как сжатое изображение, хранимое с помощью
как сжатое изображение, хранимое с помощью  слов памяти. Эти приближенные изображения для различных значений
слов памяти. Эти приближенные изображения для различных значений  приведены на рис.2,3. Выигрыш в памяти здесь составит
приведены на рис.2,3. Выигрыш в памяти здесь составит  . Результаты эксперимента приведены в табл.1.
. Результаты эксперимента приведены в табл.1.
|
|
|
Таблица 1 -
Коэффициент  малоранговой аппроксимации малоранговой аппроксимации
| Выигрыш в памяти  при использовании малоранговой аппроксимации при использовании малоранговой аппроксимации
|

| 
|

| 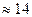
|

| 
|

| 
|
| 
|

Рис.1. Исходное изображение

Рис. 2. Сжатое изображение. Ранг аппроксимации равен 20

Рис. 3. Сжатое изображение. Ранг аппроксимации равен 160
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1112; Нарушение авторских прав?; Мы поможем в написании вашей работы!