Розділ 4. Прямі і площини

4.1. Прямі лінії на площині.

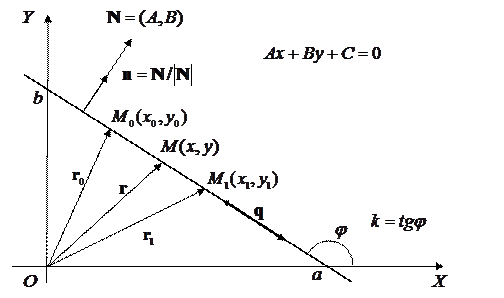
Рис. 11.1. Параметри прямої лінії на площині

Таблиця 4.1. Рівняння прямої лінії на площині

N	Назва	Рівняння
	Загальне рівняння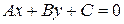
	Нормальне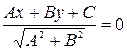
	У відрізках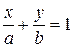
	З кутовим коефіцієнтом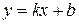
	Канонічне
	Через дві точки
	Параметричне в координатах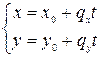
	Параметричне через дві точки
	Векторне параметричне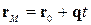
	Векторне параметричне через дві точки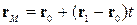
	Векторне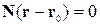

Нормаль до прямої .

Можливий вираз для напрямного вектора: , 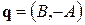і т. п.

Відрізки, що відтинаються на осях: , .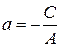

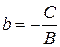Кутовий коефіцієнт: .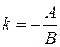

Абсолютне значення величини

визначає відстань від точки до прямій, а її знак – їхнє взаємне розташування.

4.2. Рівняння площини й прямої у просторі

Таблиця 4.2. Рівняння площини

N	Назва рівняння	Рівняння
	Загальне рівняння
	Нормальне
	У відрізках
	Векторне параметричне, задане а)одною точкою і двома напрямними векторами; б) трьома точками; в) двома точками й одним напрямним вектором.	;   ;   .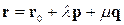
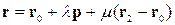	Параметричне, задане а) точкою і двома напрямними векторами;     б) трьома точками;     в) двома точками й одним напрямним вектором.	;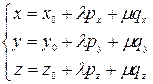
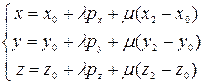
	Векторне, задане нормаллю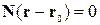
	Векторне, задане а) напрямними векторами; б) двома точками й одним напрямним вектором; в) трьома точками.	, , .
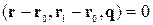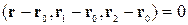	Векторне рівняння площини в координатному записі, задане а) напрямними векторами;     б) двома точками й одним напрямним вектором;   в) трьома точками.	, ,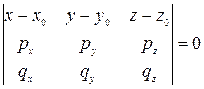

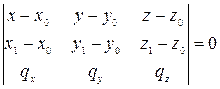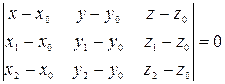
Нормаль до площини

.

Вираз нормального вектора через напрямні

.

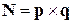Відрізки, що відтинаються на осях:

, , .

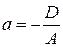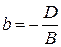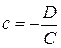Абсолютне значення величини

визначає відстань від точки до прямої, а її знак – їхнє взаємне розташування.

Таблиця 4.3. Рівняння прямої лінії в просторі.

N	Назва рівняння	Рівняння
	Векторне параметричне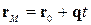
	Векторне параметричне, задане двома точками.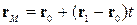
	Параметричне в координатах
	Параметричне, задане двома точками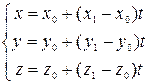
	Канонічне
	Через дві точки
	Загальне рівняння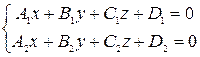
	Векторне
	Векторне, задане двома точками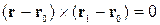

Якщо пряма задана, як перетинання двох площин, то її напрямний вектор визначають нормальними до цих площин векторами:

.

4.3. Задачі на взаємне розташування точок, прямих і площин.

У цьому розділі підручника наведено лише декілька, пов'язаних із прямими і площинами задач, що або викликають труднощі підчас розв’язання, або допускають красиві розв’язки, тобто є найбільш повчальними.

Задача 4.1. Визначить проекцію точки на пряму на площини, відстань від цієї точки до прямої. Одержіть рівняння перпендикуляра, опущеного з цієї точки на пряму.

1. Радіус-вектор точки 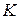– проекції заданої точки 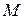на пряму представимо як різницю

.

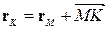Але вектор 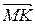– це проекція вектора 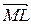на вектор нормалі, де точка 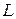‑ довільна точка на прямій:

.

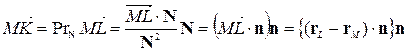Припустімо, що пряма задана своїм векторним параметричним рівнянням 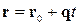. Тоді, з огляду на те, що нормальний вектор і напрямляючий ортогональні (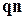= 0), для 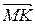одержуємо такий вираз:

Тоді для 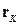одержуємо:

. (4.1.1)

Це співвідношення вирішує поставлену задачу, якщо задано нормаль і точку, через яку проходить пряма, тобто якщо задано векторне рівняння прямої.

2. Відстань від точки 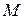до прямої дорівнює довжині вектора :

.

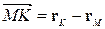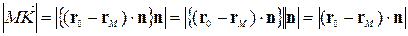Цей вираз можна легко звести до нормованого рівняння прямої.

Аналогічна задача в просторі дозволяє одержати більш красиві розв’язки, тому що в просторі ми можемо скористатися поняттям векторного добутку

Задача 4.2. Визначить проекцію точки на пряму на площини, відстань від цієї точки 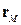до прямої 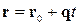. Одержіть рівняння перпендикуляра, опущеного з цієї точки на пряму.

1. Нехай точка 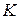є проекцією заданої точки 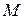на пряму:

, причому .

Тоді вектор 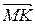є компонентом вектора 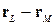перпендикулярним :

,

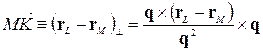де 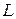‑ будь-яка точка заданої прямої.

Оскільки точка 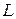належить прямій, то її радіус-вектор можна записати у вигляді , де 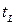– значення параметра, що відповідає точці .

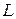Тоді для 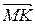одержуємо:

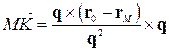. (4.2.1)

Довжина цього вектора визначає відстань 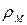від точки 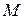до прямої:

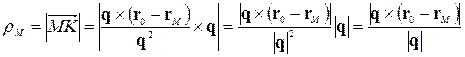. (4.2.2)

2. Можна знайти відстань від точки до прямої суто геометричним методом. З'єднаймо точку 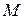з будь-якою точкою на прямій, наприклад, з точкою . Виберімо на прямій іншу точку, що не збігається з 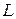, наприклад 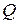(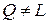), і відкладімо від точки 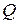відрізок 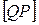, паралельний відрізкові 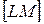, так, щоб точки 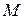і 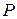виявилися в одній напівплощині.

Площа отриманого паралелограма буде дорівнює величині векторного добутку 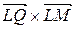, висота, проведена з точки 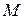до основи 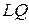, є шуканою відстанню від точки 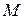до прямої. Висоту паралелограма можна знайти, розділивши його площу на довжину основи, до якого проведена ця висота:

.

У цю рівність підставимо вирази для радіусів-векторів точок 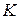і 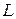, що належать прямій:

.

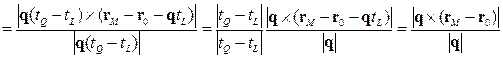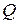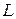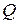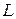Особливістю такого розв’язку є те, що як точки і можна вибирати які завгодно незбіжні точки прямої. Наприклад, можна було вибрати такі точки і , щоб 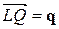, і відразу одержати шуканий результат, що збігається з (13.2.2).

3. Однак повний розв’язок цієї задачі вимагає, щоб ми знайшли ще і місце розташування точки 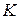– проекції точки 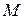на задану пряму. Цю задачу вирішимо дещо по-іншому.

Нехай точка 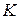на прямій задана своїм параметром:

.

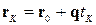Щоб знайти значення 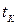, будимо вважати, що вектор 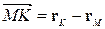ортогональний прямій, тобто 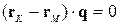. Тоді маємо

.

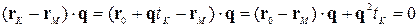Звідси одержуємо, що

.

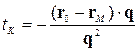Отже, радіус-вектор точки 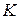дорівнює

.

Знаючи 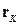можна задати рівняння перпендикуляра, наприклад, як рівняння прямої, що проходить через дві точки

Крім того, можна перевірити погодженість різних рішень. Так, для різниці, 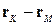ми тепер одержуємо вираз

,

з якого випливає (13.2.2).

Рис. 4.1. Відстань від точки до прямої і між перехресними прямими.

Задача 4.3. Знадіть відстань між перехресними прямими. Побудуйте рівняння загальної нормалі.

Цю задачу теж можна вирішити в три етапи. Спочатку знайдемо відстань між перехресними прямими. Потім дамо геометричне пояснення отриманої відповіді, а далі одержимо рівняння прямої – загальної нормалі до даних прямих.

1. Нехай обидві прямі задані векторними параметричними рівняннями:

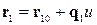і 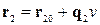, де задані радіуси-вектори точок і , через які проходять прямі, їхні напрямні вектори і 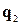. Величини 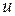і є параметрами для першої і другої прямої відповідно.

У цьому випадку відразу можна указати вектор 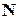, перпендикулярний обом прямим:

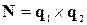
Цей вектор є напрямним вектором для загального перпендикуляра.

Тепер з’єднаймо напрямленим відрізком будь-яку точку на другій прямій 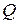з будь-якою точкою на першій прямій :

.

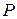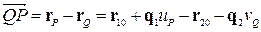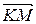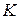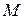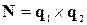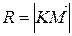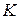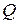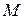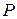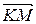Припустимо, що вектор , який з'єднує точку на другій прямій з точкою на першій, перпендикулярний обом прямим. Тоді цей вектор рівнобіжний векторові , а довжина його дорівнює шуканій відстані між прямими . У той же час точка є ортогональною проекцією точки на пряму , а точка – ортогональною проекцією точки на пряму . Отже, відрізок є не що інше, як ортогональна проекція відрізка 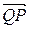на відрізок 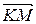або на вектор :

.

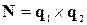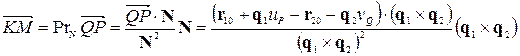Звідси для 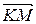одержуємо

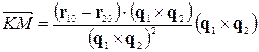. (4.3.1)

Довжина цього вектора дорівнює відстані між перехресними прямими:

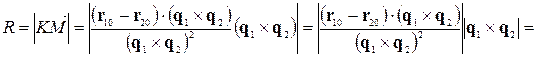
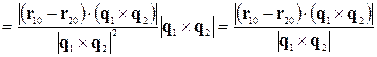. (4.3.2)

2. Геометричний зміст отриманого результату.

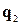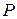Давайте одержимо вираз (4.3.2) методом, що аналогічний до приведеного в другій дії задачі 4.2. Від довільної точки другої прямої відкладімо вектори , і напрямлений відрізок , де точка – довільна точка першої прямої. Тепер побудуймо на цих трьох векторах паралелепіпед. Висота цього паралелепіпеда і буде визначати відстань між даними перехресними прямими.

Об’єм цього паралелепіпеда дорівнює модулю змішаного добутку цих трьох векторів:

,

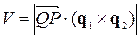а площа основи визначається величиною векторного добутку векторів , :

.

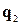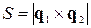Отже, висота дорівнює

.

Це співвідношення збігається з результатом (4.3.2) і пояснює його геометричний зміст.

3. Для повного розв’язку задачі нам треба визначити місце розташування точок 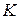і 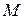, що були введені в першій дії. Ці точки є кінцями загального перпендикуляра до заданих перехресних прямих. Отже, напрямлений відрізок

перпендикулярний нормалі 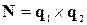, спільній для заданих прямих. Тут 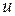– значення параметра, що відповідає точці 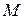, а – точці 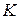. Умову перпендикулярності виразимо у вигляді рівності нулю відповідних скалярних добутків:

,

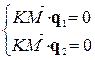
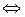
де для зручності введений вектор 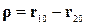. Після найпростіших перетворень одержуємо таку систему рівнянь для невідомих і :

.

Розв’язок цієї системи можна записати у вигляді

.

Тут величина 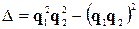можна записати у вигляді

,

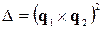отриманому в задачі 8.5. Вираз же для чисельника можна поки не спрощувати.

Для другого параметра аналогічно одержуємо:

.

Ми одержали значення параметрів, що відповідають точкам 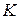і 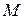, а отже, знаємо тепер радіуси-вектори цих точок і, отже,можемо побудувати рівняння загального перпендикуляра як пряму, що проходить через ці точки.

З другого боку, ми одержали ще один вираз для вектора , що повинен збігатися з раніше отриманим (13.3.1).

.

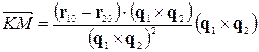Тобто ми повинні переконатися в справедливості рівності

,

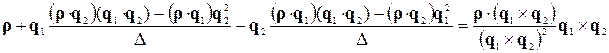яке після множення на 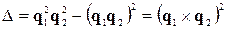набуває вигляду

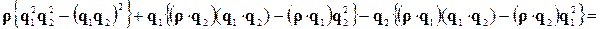
. (4.3.3)

Переконатися в тому, що ліву частину цієї рівності можна представити у вигляді правої частини можна таким способом. Представимо ліву частину цієї рівності у вигляді невідомого вектора :

.

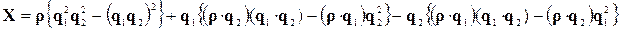Спочатку знайдений скалярний добуток множимо по черзі на вектори і на 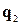і переконуємося в тому, що ці добутки дорівнюють нулю. Виходить, вектор перпендикулярний векторам на 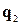, а отже, він рівнобіжний векторові і його можна представити у вигляді

.

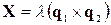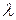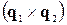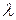Щоб знайти коефіцієнт , множимо на векторний добуток і для одержимо таке співвідношення:

.

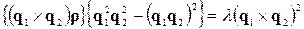Звідси знаходимо, що

.

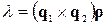Отже, вектор дорівнює

,

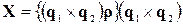що і треба було довести.

Як додаткову вправу можна довести рівність (13.3.3) шляхом послідовних прямих перетворень лівої частини в праву. Дамо лише невелику підказку. Якщо перенести перший доданок у лівій частині праворуч, то в правій частині виявиться подвійний векторний добуток деяких векторів.

Задача 4.4. Взаємне розташування прямих на площині й площин у просторі. Алгебра і геометрія.

У нашому курсі ми неодноразово говорили, що аналітична геометрія надає чудову можливість представити більшість алгебраїчних теорем і задач наочно. Розгляньмо приклад розв’язку системи двох рівнянь із двома невідомими:

.

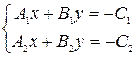Спочатку припустімо, що в правій частині цих рівнянь не стоять одні нулі, тобто хоча б один з коефіцієнтів 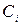не дорівнює нулю. Таку систему рівнянь називають неоднорідною системою й алгебраїчне розв’язок цієї системи добре відомий:

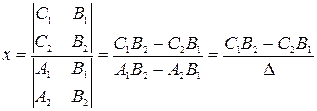
та

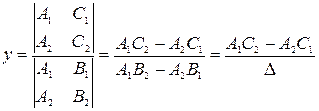
Цей розв’язок є єдиним, коли знаменники в цих виразах не дорівнюють нулю. Нагадаємо, що в знаменнику цих виразів стоїть так званий визначник системи рівнянь:

.

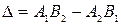Якщо знаменники дорівнюють нулеві, а чисельники не дорівнюють нулеві, то розв’язку немає. Можливий випадок, коли і чисельники, і знаменники, дорівнюють нулю, тобто виконується співвідношення

.

Тоді рівняння системи є по суті одним і тим! самим рівнянням, і система має безліч рішень, у яких невідомі виявляються залежними одна від одної. Зв'язок між змінними визначається кожним з рівнянь системи 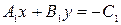, 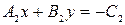або будь-яким рівнянням, отриманим з них підчас множення на ненульове число.

Усі ці висновки можна представити і геометричною мовою. Для цього досить помітити, що рівняння системи є рівняннями прямих ліній, а спільний розв’язок цих рівнянь є ні що інше, як пошук спільних точок у цих прямих.

Рівняння в системі є рівняннями прямих, записаними в загальному вигляді. Виходить, нам задані нормалі до цих ліній:

та.

Рівність нулю визначника системи виявляється еквівалентним паралельності цих векторів:

.

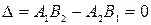
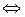
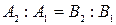
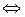
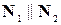Отже, якщо визначник системи не дорівнює нулю, то нормалі, а разом з ними і самі прямі не рівнобіжні одне одному, а отже, вони мають єдину точку перетинання.

Якщо визначник виявляється рівним нулю, то це рівносильно тому, що прямі виявляються рівнобіжними. Відстань 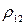між ними можна визначити з нормованого рівняння:

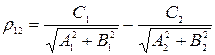
Ми бачимо, що якщо для коефіцієнтів 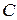справедливе таке ж відношення, що і для коефіцієнтів 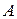і 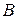, тобто

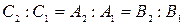
то відстань між рівнобіжними прямими дорівнює нулю. Виходить, у цьому випадку прямі збігаються і кожна з них є розв’язком системи. Якщо це співвідношення для коефіцієнтів 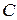не виконується, то відстань між рівнобіжними прямими не дорівнює нулю, і, отже, прямі не мають спільних точок, а система рівнянь не має розв’язку.

Рис. 4.2. Розв’язок системи рівнянь і взаємне розташування двох прямих на площині

Ми бачимо, що між алгебраїчним і геометричним підходами можлива повна еквівалентність. Через це міркування мовою площин і прямих часто використовують підчас розв’язуючи задачі в алгебрі, зокрема, системи рівнянь великого числа мінних.

Розгляньмо випадок, коли праві частини обох рівнянь дорівнюють нулю – так званий однорідний випадок. У цьому виразі ситуація дещо зворотна. Якщо визначник системи не дорівнює нулю, то можливим є тільки тривіальний розв’язок. 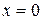та. 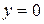Ситуація змінюється, коли визначник системи стає рівним нулю 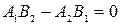. Тоді рівняння системи через пропорції знову виявляється тим самим рівнянням, що визначає всю множину розв’язків системи.

Особливо важливі такі розв’язки у фізиці, коли вирішують задачу про так звані, власні рухи якоїсь системи. Так називаються рухи системи за відсутності зовнішніх сил, що відіграють роль неоднорідностей. Тому для розв’язку таких задач потрібно дорівняти нулю визначник системи рівнянь руху цієї фізичної системи.

Задача 4.5. «Відбиття» променя від трикутника.

Ця традиційна задача про так зване трасування променями світла, що виникає підчас побудови графічних зображень у комп'ютерній графіці, де поверхні фігур задаються трикутниками.

У цій задачі потрібно визначити, чи має заданий промінь спільну точку з заданим у просторі трикутником, і знайти напрямок відбитого від цієї точки променями.

Отже, припустімо, що нам у просторі задано промінь, що виходить з точки 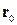з напрямним вектором . Тоді рівняння цього променя можна записати в параметричному вигляді:

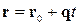, причому . (4.5.1)

Трикутник 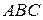у просторі задамо радіусами-векторами його вершин: ,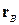і 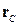. Вирішимо задачу за кілька дій.

1. Трикутник 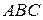визначає площину, в якій він належить. Рівняння цієї площини запишемо у векторному параметричному вигляді, вибравши як напрямляючи вектори будь-яку пару напрямлених відрізків , або :

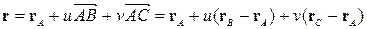. (4.5.2)

Точку перетинання променями (13.5.1) і площини (13.5.2) знайдемо, прирівнявши відповідні компоненти в цих векторних рівняннях.

. (4.5.3)

Ми одержали систему з трьох рівнянь для трьох невідомих , 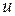і .

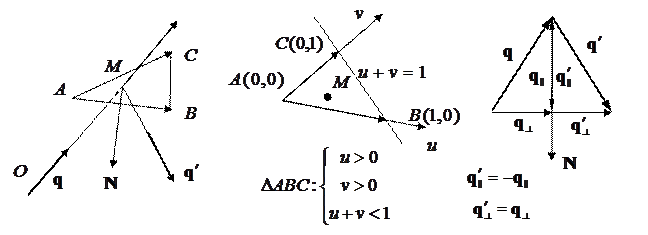
Рис. 4.3. Відбиття променя від трикутника. Афінна система в площині трикутника. Закони відбиття

Припустімо, що система має єдиний розв’язок , 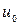і , що описують деяку точку 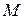перетинання променя з трикутником.

Оскільки заданий промінь відповідає позитивним значенням параметра , то величина повинна бути позитивною:

. (4.5.4)

Залишилося перевірити, чи належить ця точка трикутникові 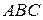. Для цього розгляньмо величини 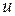і як координати на площині 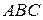у системі відліку з центром у точці 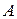й осями координат і . Вектори і є при цьому базисними векторами. Тоді координати точок трикутника 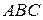у цій системі відліку задовольняють такий системі нерівностей:

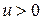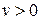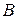, і . В останній нерівності ми використовували рівняння прямої , що з'єднує точки і 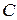. Отже, величини 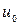і повинні задовольняти цим нерівностям:

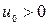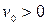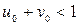, , . (4.5.5)

Припустімо, що точка 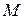виявилася всередині трикутника, і перейдімо до наступної дії.

2. Щоб знайти напрямний вектор відбитого променя, скористаємося законами відбиття. Для цього уведемо вектор нормалі 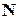до площини трикутника, виразивши його через напрямні вектори і 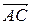цієї площини:

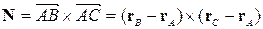. (4.5.6)

Відповідно до законів відображення проекції напрямних векторів падаючого і відбитого променів на нормаль відрізняються знаком, але збігаються за величиною, тобто:

. (4.5.7)

Поперечні ж до вектора 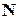компоненти напрямних векторів однакові:

. (4.5.8)

Виходить, вектор можна записати в такому вигляді:

. (4.5.9)

Це співвідношення, поряд з виразами (13.5.4)–(13.5.6) і системою (13.5.3), є розв’язком поставленої задачі.

Самостійно слід розібратися з випадком, у якому система (13.5.3) не має розв’язку.

Дата добавления: 2014-01-04