Основные понятия

Основные понятия. Высказывания и операции над ними. Пропозициональные переменные. Классификации формул алгебры высказываний.

Тема 1. ЛОГИКА ВЫСКАЗЫВАНИЙ

Цели и задачи изучения темы: Формирования представлений о таких понятиях как выказывание, булева функция, дизъюнктивные и конъюнктивные формы. Обучение составлению таблиц истинности.

Знать определения следующих понятий: логическая равносильность, нормальная форма (КНФ, СНФ, СКНФ, СДНФ)

С древнейших времен человечеству известна логика, или искусство правильно рассуждать. Имея какие-то утверждения (посылки), истинность которых проверена, скажем, на опыте, логик путем умозрительных построений приходит к другому утвержде­нию (заключению), которое также оказывается истинным (в некоторых случаях). Опыт древних (чисто наблюдательный) был систематизирован Аристотелем. Он рассмотрел конкретные виды рассуждений, которые назвал силлогизмами. А именно, Аристотель рассмотрел так называемые категорические утверждения четырех видов:

все А обладают свойством В (все А суть В);

некоторые А обладают свойством В (некоторые А суть В);

все А не обладают свойством В (все А суть не В)

некоторые А не обладают свойством В (некоторые А суть не В)

и зафиксировал все случаи, когда из посылок такого вида выводятся заключения одного из этих же видов.

Пример:

Все люди смертны. Сократ — человек. Следовательно, Сократ смертен. Это рассуждение правильно, потому что подходит под один из образцов силлогизмов Аристотеля.

Все дикари раскрашивают свои лица. Некоторые современные женщины раскрашивают свои лица. Следовательно, некоторые современные женщины -дикари. Это рассуждение неправильно, хотя, видимо, все входящие в него утверждения истинны.

Логика Аристотеля - это классическая логика.

Математическая логика с внешней стороны отличается от «обычной» тем, что она широко пользуется языком математических и логических знаков, исходя из того, что в принципе они могут совсем заменить слова обычного языка и принятые в обычных живых языках способы объединения слов в предложения. Довольно рано возникла идея о том, что, записав все исходные допущения на языке специальных знаков, похожих на математические, можно заменять рассуждение вычислением. Точно же сформулированные правила таких логических вычислений можно перевести на язык вычислительной машины, которая тогда будет способна автоматически выдавать интересующие нас следствия из введенных в нее исходных допущений.

Более определенный и близкий к реально существующему универсальному логическому исчислению развивал Лейбниц (1646-1716). Лейбниц надеялся даже, что в будущем философы вместо того, чтобы бесплодно спорить, будут брать бумагу и вычислять, кто из них прав.

Начало созданию того аппарата математической логики, который теперь называется логикой высказываний, положил Джордж Буль (1815—1864).

Логико-математические языки и теория их смысла были затем значительно развиты в работах Фреге (1848-1925). Широко задуманное изложение больших разделов математики на языке математической логики было предпринято в работах Пеано (1858—1932) и особенно в фундаментальной трехтомной монографии Рассела и Уайтхеда, изданной в 1910-1913 гг. В двадцатых годах XX века с программой обоснования математики на базе математической логики выступил знаменитый математик Гильберт (1862-1943).

С этого времени и начинается современный этап развития математической логики.

Подъем широкого интереса к математической логике не только среди математиков, но и среди техников произошел тогда, когда обнаружилось, что в рамках математической логики уже создан аппарат для расчета действия самых различных вычислительных и управляющих дискретных устройств.

В математической логике предметом исследования часто оказываются математические теории, такие как математический анализ, алгебра, элементарная геометрия, арифметика и др. В логике математические теории изучаются в целом - и это одна из особенностей математической логики по сравнению с другими математическими дисциплинами.

Логика высказываний лежит в основе всех других разделов математической логики и необходима для их понимания. Логика высказываний строится так же, как и многочисленные математические теории. В качестве основных понятий берется некоторый класс объектов, а также некоторые свойства, отношения и операции над этими объектами. Эти основные понятия рассматриваются как исходные, не требующие внутри самой теории какого-либо определения. С другой стороны, они выбираются не произвольным образом, а так, чтобы соответствовать тому внематематическому содержанию, которое должна описывать математическая теория.

Элементами логических рассуждений являются утверждения, которые либо истинны, либо ложны, но не то и другое вместе. Такие утверждения называются (простыми) высказываниями. Простые высказывания обозначаются пропозициональными переменными, принимающими истинностные значения «И» и «Л». Из простых высказываний с помощью логических связок могут быть построены составные высказывания. Обычно рассматривают следующие логические связки:

Название Прочтение Обозначение

Отрицание не −,­

Конъюнкция и &,^

Дизъюнкция или V

Импликация если... то

Эквивалентность тогда и только, когда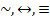

Правильно построенные составные высказывания называются (пропозициональными) формулами.

Договоримся обозначать конкретные высказывания начальными заглавными буквами латинского алфавита А, В, С, Д... или теми же буквами с индексами внизу.

Приведем примеры высказываний:

А₁ «Москва — столица России»;

А₂: «Саратов находится на берегу Невы»;

А₃: «Все люди смертны»;

А₄: «Сократ — человек»;

А₅: «7 < 4»;

Из простых высказываний путем некоторого числа логических операций можно строить сложные высказывания.

Например, из простых высказываний:

A) «Радиостанция работает,

B) «Наш радиоприемник включен»,

C) «Наш радиоприемник настроен на волну радиостанции»,

D) «Мы находимся у радиоприемника»,

E) «Мы слушаем радиопередачу»

можно построить сложное высказывание:

F) «(Радиостанция работает) и {наш радиоприемник включен) и {наш приемник настроен на волну радиостанции) и {мы находимся у радиоприемника) и {мы слушаем радиопередачу)».

Действие операции отрицания представим в виде следующей таблицы истинности для отрицания:

А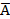
И	Л
Л	И

Именно эту таблицу мы и примем в качестве определения операции отрицания. Подобными таблицами мы будем пользоваться и при определении других логических операций. Они называются таблицами (или матрицами) истинности.

Логика высказываний обычно отвлекается от содержания простых высказываний и рассматривает только их значения истинности. Тем самым логические операции обычно не выражают связи между содержанием высказываний. Логическая операция, образующая из двух высказываний А и B сложное.высказывание, определяет, таким образом, только отношение между значениями истинности высказываний А и B и значением истинности составленного из них сложного высказывания.

Одной из важнейших операций логики высказываний является импликация. В качестве знака для этой операции мы будем употреблять символ.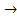

Импликация определяется следующим образом:

Если A и B два высказывания, то A B Читается А имплицирует B - сложное высказывание, которое истинно всегда, кроме того случая, когда A истинно, а B ложно.

В импликации первый член A называется антецедентом, второй B — консеквентом.

Истинное значение формулы определяется через истинностные значения ее состовляющих в соответствии со следующей таблицей:

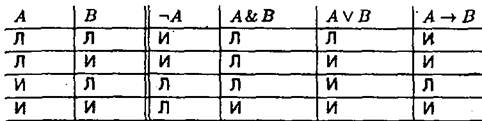
Дата добавления: 2014-01-04