Предикаты и формулы

Тема 2. О ЛОГИКЕ ПРЕДИКАТОВ

Цели и задачи изучения темы: В данной теме рассматриваются основы логики предикатов. Логика предикатов – это расширение возможностей логики высказываний, позволяющее строить высказывания с учетом свойств изучаемых объектов или отношений между ними.

Одноместный предикат Р(x) — это утверждение об объекте x, где x рассматривается как переменная. Иначе говоря, если в Р(х) вместо х подставить конкретный изучаемый объект а, то получаем высказывание, принадлежащее алгебре высказываний. В таком случае Р(а) = 1 или Р(а) = 0.

Предикаты будем обозначать заглавными латинскими буквами, переменные — строчными буквами из конца латинского алфавита (x, у, z,...), константы — строчными буквами из начала латинского алфавита (а, b, с,...).

Многоместный предикат Р(х ₁,...,x_n)—это утверждение об объектах х₁,..., х_п, где х₁,..., х_п рассматриваются как переменные. Следовательно, при подстановке конкретных значений a₁,..., а_п получим высказывание Р(а₁,..., а_п), являющееся истинным или ложным.

Для получения высказываний из предикатов помимо подстановки вместо переменных конкретных объектов применяются также кванторы: квантор всеобщности «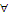» и квантор существования « ».

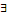Символ ««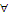x» интерпретируется как фраза «для всех x»

При добавлении к предикату Р( x) квантора всеобщности мы получим высказывание 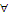xР(x). Оно примет истинное значение, если предикат Р(x) выполняется для всех объектов а₁, а₂,..., а_i,..., которые можно подставить вместо х. Это можно записать как

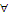х Р(х) = Р(а₁) & Р(а₂) &... & Р(а_i) &...

Символ «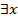» представляет фразу «существует х»

При добавлении данного квантора к предикату получаем также высказывание 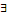х Р(х). Данное высказывание будет истинным, если предикат Р(х) выполняется хотя бы для одного из объектов a₁, a_2,.., a_i,..., которые можно подставить вместо х. Это можно записать как

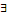х Р(х) = P(a₁) V P(a₂) V... V Р( a_i ) V...

Переменная x, входящая в формулу, называется связанной, если она находится под действием квантора 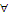x или 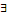х. В противном случае, переменная х в формуле является свободной. Например, в формулах 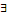х(х = у) и 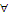хВ(х,у) переменная х связанная, а пере­менная у свободная. Очевидно, что формула без свободных переменных является высказыванием.

Пример 2.1. D(xl,x2) = «Натуральное число xl делится (без остатка) на натуральное число х2» - двуместный предикат, определенный на множестве пар натуральных чисел M=NxN. Очевидно, D(4,2) = И, D(3,5) = 0.

Пример 2.2, Q(x) ==«х2<-1, x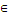R» — одноместный предикат, определенный на множестве действительных чисел M=R. Ясно, что Q(- 1) = Л, Q(5) = Л, и вообще предикат Q(x) — тождественно ложен, т. е. Q(x) = Л для всех x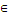R.

Пример 2.3. B(x,y,z) =«x2+y2<z; x,y,z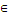R.» — трехместный предикат, определенный на R3. B(1,1,-2)=Л, В(1,1,2)=И.

Предикат Р, определенный на М, называется тождественно истинным, если он принимает значение И при любых значениях предметных переменных; Предикат Р называется тождественно ложным, если он принимает значение Л при любых значениях предметных переменных. Предикат Q из примера 2.2. является тождественно ложным.

Поскольку предикаты — это функции со значениями во множестве высказываний, где введены логические операции, то эти операции естественно определяются и для предикатов. Пусть Р и Q — предикаты, определенные на М. Тогда

1. ┐Р(х,х₂,...,х_n) = Р(х₁,х₂,...,х_n)

2. (P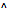Q)(x₁,x₂,...,x_n) = P(x₁,x₂,...,x_n)^Q(x₁,x₂,...,x_n)

3. (PVQ)(x₁,x₂,...,x_n) = P(x₁,x₂,...,x_n)VQ(x„x₂,...,x_n)

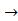4. (Р Q)(x₁x₂,...,x_n) = P(x₁,x₂,...,x_n) Q(x₁,x₂,...,x_n)

Предикаты P и Q, определенные на M, называются равносильными (пишут P=Q), если P(x₁,x₂,...,x_n):=Q(x₁,X₂,...,x_n) для любого набора (х₁,х₂,...,х_n) предметных переменных из М.

Теорема 2.1 Множество n-местных предикатов, определенных на М, образует булеву алгебру предикатов. Т.о., для них справедливы основные эквивалентности.

Дата добавления: 2014-01-04