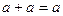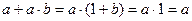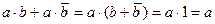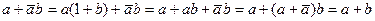Представление ФРС в виде дизъюнктивной нормальной формы. КПУФ и МСО

В результате применения методов, описанных в пунктах 4.3.2, 4.3.3 и 4.3.4 мы получаем ФРС в виде функции алгебры логики . Эта функция может иметь разный вид, в частности содержать вынесенные множители, скобки и т.п. Для дальнейшего получения на основе ФРС функции готовности, а также для анализа структуры системы удобно перевести ФРС в вид дизъюнктивной нормальной формы:

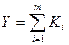- логическая сумма (дизъюнкция) , где - это логическое произведение (конъюнкция) переменных 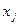и .

Например, в результате анализа мостиковой схемы была получена ФРС в виде:

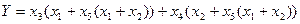
Чтобы привести ФРС к виду ДНФ просто раскроем все скобки:

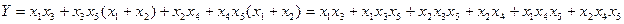В полученной ДНФ содержится 6 конъюнкций.

Рангом конъюнкции называет количество множителей в конъюнкции. Например, . Рангом ДНФ называется сумма рангов отдельных конъюнкций 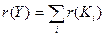. Для нашего примера .

Одна и та же логическая функция может быть представлена в виде ДНФ различными способами. Среди них можно выделить следующие частые случаи:

• минимальная дизъюнктивная нормальная форма (МДНФ) – такая ДНФ, ранг которой минимален среди других возможных ДНФ;
• ортогональная дизъюнктивная нормальная форма (ОДНФ) – такая ДНФ, у которой все входящие в неё конъюнкции взамно ортогональны: ;
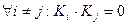• совершенная дизъюнктивная нормальная форма (СДНФ) – такая ДНФ, все конъюнкции которой имеет ранг, равный количесту агрументов функции:

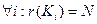
Привести произвольную ДНФ к виду МДНФ можно следуя правилам алгебры логики:

• 

• 
• 
• 

Для рассматриваемого примера получаем МДНФ ранга 10:

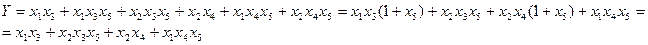
Если ФРС представлена в виде МДНФ, то каждая конъюнкция будет соответствовать одному из кратчайших путей успешного функционирования (КПУФ).

Действительно, конъюнция МДНФ содержит в себе наименьший возможный набор множителей, каждый из которых является переменной состояния того элемента, который должен быть исправен. Для рассматриваемого примера существуют 4 КПУФ: (1,3), (2,3,5), (2,4) и (1,4,5).

Функций неработоспособности системы (ФНС) называется функция алгебры логики от переменных состояния элементов 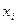, которая равна единице, если при заданных состояниях элементов система неработоспособна, и нулю в противном случае.

Фактически, ФНС является дополнением (логическим отрицанием) ФРС: . Получим ФНС для нашего примера:

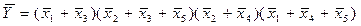и приведем её к виду МДНФ, раскрывая скобки и сокращая размер выражения, пользуясь правилами алгебры логики:

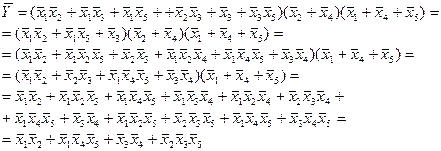
Если ФНС представлена в виде МДНФ, то каждая конъюнкция будет соответствовать одному из минимальных сечений отказов (МСО).

Следуя той же логике, что и в случае КПУФ, рассуждаем: конъюнция ФНС в МДНФ содержит в себе наименьший возможный набор множителей, каждый из которых является отрицанием переменной состояния того элемента, который должен быть неисправен. Для рассматриваемого примера существуют 4 МСО: (1,2), (1,4,5), (3,4) и (2,3,5).

Представление ФРС и ФНС в виде МДНФ удобно, т.к.:

• выражения имеют наименьшую длину;
• конъюнкции в выражениях соответствуют КПУФ и МСО системы.

Дата добавления: 2014-01-03