
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Момент сили відносно точки
|
|
|
|
Контрольні запитання
1. Що називається в’язью?
2. В чому полягає принцип звільнення від в’язів?
3. Перерахуйте основні типи в’язів, для яких напрями дії реакцій відомі?
4. Вкажіть в’язі, які мають одну реакцію? Дві реакції? Три реакції?
Моментом сили  відносно точки
відносно точки  називається фізична величина, яка характеризує здатність сили викликати обертальній рух тіла відносно даної точки і визначається векторним добутком векторів
називається фізична величина, яка характеризує здатність сили викликати обертальній рух тіла відносно даної точки і визначається векторним добутком векторів 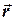 та
та 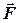
 (3.1)
(3.1)
 де
де 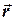 – вектор, проведений з даної точки
– вектор, проведений з даної точки  у точку
у точку 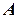 прикладання сили. Згідно з властивостями векторного добутку вектор
прикладання сили. Згідно з властивостями векторного добутку вектор 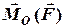 перпендикулярний площині, в якій лежать вектори
перпендикулярний площині, в якій лежать вектори 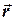 та
та  (рис. 3.1) та його модуль
(рис. 3.1) та його модуль
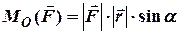 . (3.2)
. (3.2)
Модуль моменту сили залежить від орієнтації векторів 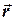 та
та  , має макси-мальне значення
, має макси-мальне значення 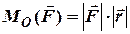 , коли вектори перпендикулярні і дорівнює нулю коли вони паралельні, тобто лінія дії сили проходить через точку
, коли вектори перпендикулярні і дорівнює нулю коли вони паралельні, тобто лінія дії сили проходить через точку  . Момент сили вимірюється в ньютоно-метрах.
. Момент сили вимірюється в ньютоно-метрах.
Сила  є ковзний вектор, тому момент сили відносно точки не змінюється при переміщенні точки прикладання сили вздовж лінії її дії, наприклад, коли силу
є ковзний вектор, тому момент сили відносно точки не змінюється при переміщенні точки прикладання сили вздовж лінії її дії, наприклад, коли силу  перенести з точки
перенести з точки 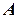 в точку
в точку 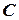 (рис. 3.1).
(рис. 3.1).
Вкажемо різні способи знаходження вектора моменту сили. В площині, де лежать вектори 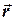 та
та  введемо декартову систему координат
введемо декартову систему координат  , сумістивши початок координат з точкою
, сумістивши початок координат з точкою 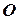 (рис.3.2).
(рис.3.2).
1. З точки 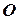 проведемо перпендикуляр на лінію дії сили (рис. 3.2а). Від-стань
проведемо перпендикуляр на лінію дії сили (рис. 3.2а). Від-стань 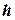 від заданої точки
від заданої точки 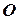 до лінії дії сили називається плечем
до лінії дії сили називається плечем

 . (3.3)
. (3.3)
Для визначення напряму можливого обертання твердого тіла під дією сили навколо заданої точки замість вектора моменту, який перпендикулярний площині  , використовують його алгебраїчне значення
, використовують його алгебраїчне значення
 , (3.4)
, (3.4)
яке визначається добутком модуля сили на плече. Знак плюс береться, коли сила викликає обертання тіла навколо точки 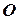 проти напряму руху стрілки годинника (тоді вектор
проти напряму руху стрілки годинника (тоді вектор  напрямлений до нас) і мінус – коли за напрямом руху стрілки годинника (тоді вектор
напрямлений до нас) і мінус – коли за напрямом руху стрілки годинника (тоді вектор  напрямлений від нас). Взаємна орієнтація векторів
напрямлений від нас). Взаємна орієнтація векторів 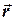 та
та  , що зображена на рис. 3.2а, відповідає випадку
, що зображена на рис. 3.2а, відповідає випадку  .
.
|
|
|
3. Зручно знаходити момент сили відносно точки використовуючи теорему Варіньона. Для цього силу  розкладають на складові
розкладають на складові 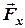 та
та 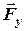 і визначають алгебраїчне значення моменту, як суму моментів, які створюють ці складові відносно точки
і визначають алгебраїчне значення моменту, як суму моментів, які створюють ці складові відносно точки 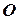 (рис.3.2б)
(рис.3.2б)
 =
= 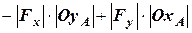 , (3.5)
, (3.5)
де у першому доданку взяли знак “–” оскільки складова 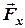 (яка має плече
(яка має плече  ) намагається повертати тіло відносно точки
) намагається повертати тіло відносно точки 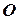 за рухом стрілки годинника та знак “+” у другому доданку, бо складова
за рухом стрілки годинника та знак “+” у другому доданку, бо складова 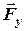 (якамає плече
(якамає плече  ) намагається повертати тіло відносно точки
) намагається повертати тіло відносно точки 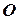 проти руху стрілки годинника.
проти руху стрілки годинника.
 Моментом сили
Моментом сили  відносно осіназивається проекція на цю вісь вектора моменту сили
відносно осіназивається проекція на цю вісь вектора моменту сили 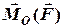 відносно точки
відносно точки  початку координат:
початку координат:
 ,
,
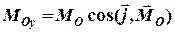 , (3.6)
, (3.6)

де 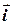 ,
,  ,
,  - орти осей координат (рис. 3.3). Ця фізична величина характеризує здатність сили викликати обертальний рух тіла навколо заданої осі.
- орти осей координат (рис. 3.3). Ця фізична величина характеризує здатність сили викликати обертальний рух тіла навколо заданої осі.
Аналітичні вирази для моментів сили  відносно декартових осей отриму-ємо як компоненти вектора
відносно декартових осей отриму-ємо як компоненти вектора 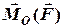
 =
= 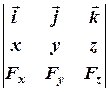 =
=  , (3.7)
, (3.7)
де 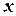 ,
,  ,
, 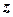 - декартові координати точки прикладання сили;
- декартові координати точки прикладання сили; 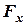 ,
, 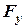 ,
, 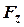 - алгебраїчні проекції сили на ці осі. Отож
- алгебраїчні проекції сили на ці осі. Отож
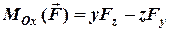 ,
,
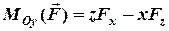 , (3.8)
, (3.8)
 .
.
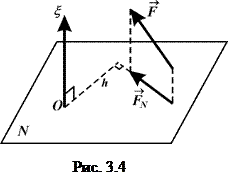 Аналізуючи формули (3.8), отримуємо ще один спосіб знаходження моменту сили відносно осі (рис. 3.4), яким користуються на практиці:
Аналізуючи формули (3.8), отримуємо ще один спосіб знаходження моменту сили відносно осі (рис. 3.4), яким користуються на практиці:
1) проводимо площину 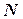 , перпендикулярну вибраній осі
, перпендикулярну вибраній осі  і знаходимо точку
і знаходимо точку 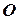 перетину цієї площини з віссю
перетину цієї площини з віссю  ;
;
2) визначаємо геометричну проекцію  си-
си-
ли  на вказану площину;
на вказану площину;
3) обчислюємо момент геометричної проекції  відносно точки
відносно точки 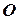 (множимо
(множимо  на плече
на плече 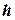 - довжину перпендикуляра, опущеного із точки
- довжину перпендикуляра, опущеного із точки 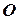 на проекцію
на проекцію 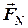 )
)
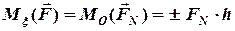 . (3.9)
. (3.9)
4) одержаному добутку приписується знак плюс, якщо із додатного напряму осі  видно, що сила прагне обертати тіло навколо осі проти руху стрілки годинника, а знак мінус – коли за рухом стрілки годинника.
видно, що сила прагне обертати тіло навколо осі проти руху стрілки годинника, а знак мінус – коли за рухом стрілки годинника.
|
|
|
Взаємній орієнтації осі  та сили
та сили  , які зображені на рис. 3.4, відповідає випадок
, які зображені на рис. 3.4, відповідає випадок 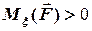 , тому
, тому  .
.
Отже, на практиці момент сили відносно осі, визначається як алгебраїчне значення добутку модуля проекції сили 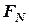 на плече
на плече 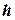 відносно точки
відносно точки 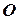 перетину осі з площиною.
перетину осі з площиною.
Момент сили відносно осі дорівнює нулю у двох випадках:
а) коли  – проекція сили на площину, яка перпендикулярна осі, дорівнює нулю, тобто коли сила
– проекція сили на площину, яка перпендикулярна осі, дорівнює нулю, тобто коли сила  і вісь
і вісь  паралельні;
паралельні;
б) коли  – плече проекції дорівнює нулю, тобто коли проекція сили
– плече проекції дорівнює нулю, тобто коли проекція сили 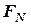 проходить через точку
проходить через точку 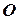 , а це означає, що лінія дії сили
, а це означає, що лінія дії сили  перетинає вісь.
перетинає вісь.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 24376; Нарушение авторских прав?; Мы поможем в написании вашей работы!