Центр ваги тіла

Центром ваги твердого тіла називається точка, до якої прикладена рівнодіюча сила однорідного поля тяжіння. Ця точка не обов’язково знаходиться в тілі, наприклад, для кільця центр ваги розташований за межами твердого тіла. Визначення центра ваги тіла є важливою задачею при проектуванні та експлуатації суден, оскільки взаємне положення центра ваги судна та його метацентру визначає остійність судна.

Якщо тіло однорідне (маса рівномірно розподілена по його об’єму) та має вісь (площину або точку) симетрії, то центр ваги знаходиться на цій осі (площині або в цій точці). Якщо тіло несиметричне, або неоднорідне, то його розбивають на сукупність 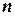елементів, для яких координати центра ваги можна легко встановити, а центр ваги тіла знаходять за наступними формулами:

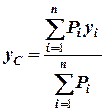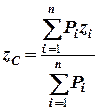, , . (5.1)

тут: 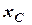, , - координати центра ваги тіла, 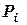- вага елемента, , , 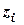- координати центра ваги - того елемента.

Зауважимо, що коли тіло має вирізи, то його вага 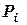входить у розрахунки за формулою (5.1) зі знаком „–”.

Для однорідних тіл формули (5.1) можуть бути спрощені. Для однорідного трьохмірного тіла з питомою вагою , , 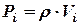тому в формулах (9.1) замість ваги елемента можна підставляти його об’єм 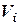. Для двомірного (плоского) тіла з поверхневою вагою , , тому замість можна користуватися площею елемента . Для лінійних однорідних тіл замість ваги елемента можна користуватися його довжиною .

Нагадаємо формули, які визначають положення центра ваги однорідних тіл, що мають правильну форму:

1) центр ваги однорідного стрижня довжиною 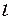з координатами кінців (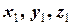) та (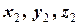) знаходиться на його середині, тому:

, , , (5.2)

2) центр ваги однорідноїдуги радіуса 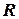та кутом при вершині 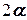– на бісектрисі кутапри вершині (рис. 5.1) на відстані ОС від центру дуги:

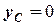, , (5.3)

де кут 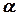вимірюється у радіанах;

3) центр ваги однорідного паралелограма з координатами вершин () – в точці перетину діагоналей:

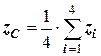, , , (5.4)

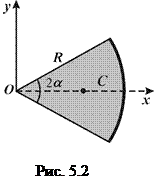
4) центр ваги однорідного трикутника, вершини якого мають координати (), – в точці перетину медіан, де вони діляться у відношенні 1:2, тому координати центру ваги трикутника знаходимо за формулами:

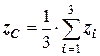, , , (5.5)

5) центр ваги однорідного сектора радіусом 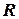та кутом при вершині 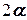– на бісектрисі кута при вершині (рис. 5.2):

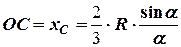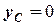, , (5.6)

де вісь 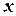- бісектриса кута при вершині, а кут 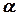вимірюється у радіанах;

Дата добавления: 2014-01-04