Решение двойственной задачи ЛП

Двойственная задача ЛП

Двойственная задача ЛП может быть сформулирована следующим образом:

найти переменные y _i (i = 1, 2,..., m), при которых целевая функция была бы минимальной

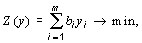
не нарушая ограничений

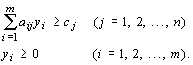
Данная задача называется двойственной (симметричной) по отношению к прямой задаче, сформулированной во втором параграфе данной главы. Однако правильным будет и обратное утверждение, так как обе задачи равноправны. Компоненты решения двойственной задачи называются объективно обусловленными оценками.

Прямая и обратная задачи ЛП связаны между собой теоремами двойственности.

Первая теорема двойственности. Если обе задачи имеют допустимые решения, то они имеют и оптимальное решение, причем значение целевых функций у них будет одинаково

или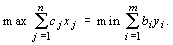

Если же хотя бы одна из задач не имеет допустимого решения, то ни одна из них не имеет оптимального решения.

Вторая теорема двойственности (теорема о дополняющей нежесткости). Для того чтобы векторы и были оптимальными решениями соответственно прямой и двойственной задачи, необходимо и достаточно, чтобы выполнялись следующие условия:

		(1)
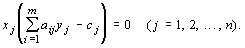
		(2)

Следствие 1. Пусть оптимальное значение некоторой переменной двойственной задачи строго положительно

Тогда из условия (1) получим

или

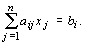
Экономический смысл данных выражений можно интерпретировать в следующей редакции. Если объективно обусловленная оценка некоторого ресурса больше нуля (строго положительна), то этот ресурс полностью (без остатка) расходуется в процессе выполнения оптимального плана.

Следствие 2. Пусть для оптимального значения некоторой переменной x _i прямой задачи выполняется условие строгого неравенства

Тогда, основываясь на том же первом условии (1), можно заключить, что y _i = 0.

Экономически это означает, что если в оптимальном плане какой-то ресурс используется не полностью, то его объективно обусловленная оценка обязательно равна нулю.

Оптимизационная модель прямой задачи линейного программирования выглядит так:

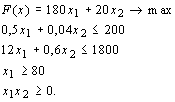
В системе неравенств должны быть однотипные знаки меньше или равно. Поэтому неравенство x ₁ ≥ 80 умножим на - 1 и поменяем знак неравенства на противоположный.

Оптимизационная модель обратной задачи линейного программирования выглядит так:

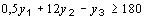
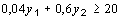
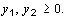
Ограничение на целочисленность переменных здесь не требуется.

Решение прямой задачи дало следующие результаты:

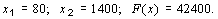
В результате решения двойственной задачи получим

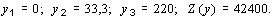
Объективно обусловленная оценка y ₁ = 0 указывает на то, что у нас избыток древесины: y ₂ = 33,3, т.е. больше нуля. Значит этот ресурс (труд) полностью используется в оптимальном плане. Значение целевой функции Z (y) равно F (x) = 42400. Это свидетельствует о том, что найденное решение оптимально.

Дата добавления: 2014-01-04