
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предел числовой функции
|
|
|
|
.
Таким образом, в конечном итоге каждому значению 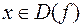 ставится в соответствие (посредством промежуточной переменной
ставится в соответствие (посредством промежуточной переменной  ) одно определенное значение
) одно определенное значение 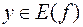 , где
, где  — множеством значений функции
— множеством значений функции 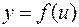 .
.
В этом случае  называют сложной функцией аргумента
называют сложной функцией аргумента  или функцией от функции (записывают
или функцией от функции (записывают 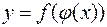 ) или композицией функций
) или композицией функций 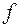 и
и 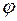 (записывают
(записывают  ). При этом функцию
). При этом функцию 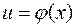 называют промежуточным аргументом,
называют промежуточным аргументом,  — независимой переменной.
— независимой переменной.
Например, функция 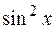 является сложной. Ее можно записать в виде цепочки равенств:
является сложной. Ее можно записать в виде цепочки равенств:
 ,
,  .
.
Аналогично можно составить сложную функцию с двумя и более промежуточными аргументами. являющуюся композицией более трех функций.
Конечный предел функции при 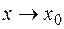 . Пусть функция
. Пусть функция 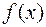 определена в проколотой окрестности точки
определена в проколотой окрестности точки  , т. е. на множестве
, т. е. на множестве 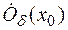
 . В точке
. В точке  значение
значение  может быть не определено.
может быть не определено.
Дадим определение конечного предела функции при 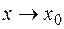 на языке «
на языке «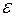 —
— 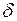 » (по Коши).
» (по Коши).
Определение. Число 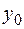 называется пределом функции
называется пределом функции  в точке
в точке  (или при
(или при 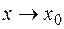 ), если для
), если для  >0 можно указать такое число
>0 можно указать такое число 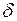 (
(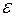 )>0, что при всех
)>0, что при всех  , удовлетворяющих условию
, удовлетворяющих условию 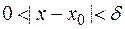 , выполняется неравенство
, выполняется неравенство  , или, в более краткой записи:
, или, в более краткой записи: 
В определении используются понятия 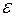 -окрестности и проколотой
-окрестности и проколотой 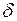 -окрестности, поэтому его и называют определением на языке «
-окрестности, поэтому его и называют определением на языке «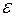 —
— 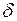 » и кратко записывают так:
» и кратко записывают так:
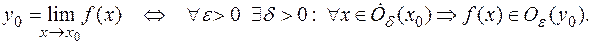
Геометрическая интерпретация определения конечного предела функции по Коши дана на рисунке.

Из рисунка видно, что  отображается функцией в
отображается функцией в  , т. е. любому
, т. е. любому  из проколотой
из проколотой 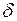 -окрестности точки
-окрестности точки  соответствует значение
соответствует значение 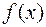 , попадающее в
, попадающее в 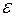 -окрестность точки
-окрестность точки 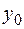 .
.
Односторонние пределы функции. При рассмотрении конечного предела функции при 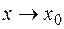 предполагалось, что точка
предполагалось, что точка  , приближаясь к
, приближаясь к  , могла оставаться как слева, так и справа от нее.
, могла оставаться как слева, так и справа от нее.
|
|
|
Иногда приходится рассматривать предел функции 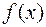 при условии, что точка
при условии, что точка  , приближаясь к точке
, приближаясь к точке  , остается либо правее, либо левее ее.
, остается либо правее, либо левее ее.
Введем понятие левой и правой окрестностей точки  .
.
Определение. Левой 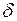 -окрестностью точки
-окрестностью точки  (обозначается
(обозначается 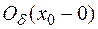 ) называется множество всех
) называется множество всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству
0b
|
 <
<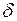 .
.
Т.е. 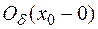 = {
= { | 0b
| 0b
|
 <
<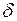 }.
}.
Проколотая левая 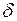 -окрестность получается «выкалыванием» из
-окрестность получается «выкалыванием» из 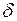 -окрестности точки
-окрестности точки  ,
,
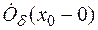 = {
= { | 0<
| 0<
|
 <
<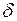 }.
}.
Аналогично определяется и правая 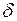 -окрестность.
-окрестность.
Определение. Число 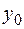 называется левым пределом (левосторонним пределом или пределом слева) функции
называется левым пределом (левосторонним пределом или пределом слева) функции  в точке
в точке  , если для любого
, если для любого  > 0 существует
> 0 существует 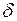 =
=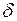 (
(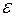 )>0, такое, что для
)>0, такое, что для 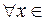
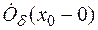

Обозначают предел слева  .
.
Аналогично определяется правый предел  функции
функции 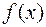 в точке
в точке  .
.
Замечание. Если в точке  функция
функция 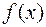 имеет конечные правый и левый пределы и они равны между собой, то это число является пределом функции в точке
имеет конечные правый и левый пределы и они равны между собой, то это число является пределом функции в точке  :
:
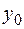 =
=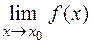
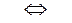
 =
= =
=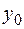 .
.
Конечный предел функции при 
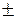 ¥.
¥.
Определение. Число 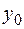 называется пределом функции
называется пределом функции  при
при  +¥, если для любого
+¥, если для любого 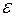 >0 существует положительное число
>0 существует положительное число 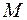 , такое, что неравенство
, такое, что неравенство  выполняется для всех
выполняется для всех  , при которых
, при которых  >
>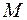 .
.
Аналогично определяетcя предел и при  –¥
–¥
Множество { |
| >
>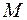 } =
} = 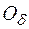 (+¥) называют
(+¥) называют 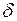 -окрестностью бесконечно удаленной точки.
-окрестностью бесконечно удаленной точки.
Бесконечные пределы функции при 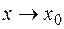 . Рассмотрим случай, когда функция
. Рассмотрим случай, когда функция  при
при 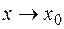 по абсолютной величине неограниченно возрастает. Такая функция не имеет конечного предела, поэтому необходимо обобщить понятие предела функции.
по абсолютной величине неограниченно возрастает. Такая функция не имеет конечного предела, поэтому необходимо обобщить понятие предела функции.
Определение. Предел функции  при
при 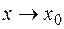 называется бесконечным, если для любого положительного числа
называется бесконечным, если для любого положительного числа 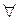
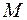 >0 существует число
>0 существует число 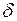 > 0, такое, что для всех значений
> 0, такое, что для всех значений  , удовлетворяющих неравенству
, удовлетворяющих неравенству 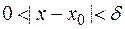 , будет выполняться неравенство |
, будет выполняться неравенство |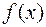 | >
| > 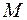 .
.
Если 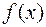 стремится к бесконечности при
стремится к бесконечности при 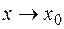 , то ее называют бесконечно большой функцией и пишут
, то ее называют бесконечно большой функцией и пишут
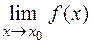 =¥
=¥
Если 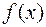 стремится к бесконечности при
стремится к бесконечности при 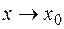 и при этом принимает только положительные или только отрицательные значения, пишут соответственно:
и при этом принимает только положительные или только отрицательные значения, пишут соответственно:
|
|
|
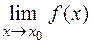 =+¥ или
=+¥ или 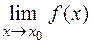 =–¥
=–¥
Бесконечный предел функции при 
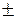 ¥.
¥.
Определение. Предел функции  при
при  +¥ (или
+¥ (или  –¥) называется бесконечным, если для любого сколь угодно большого числа
–¥) называется бесконечным, если для любого сколь угодно большого числа 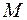 найдется такое число
найдется такое число 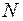 > 0, что неравенство |
> 0, что неравенство |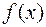 | >
| >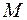 выполняется для любого
выполняется для любого  , для которого |
, для которого | | >
| >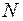 :
:
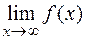 =¥
=¥ 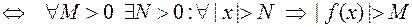 .
.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 531; Нарушение авторских прав?; Мы поможем в написании вашей работы!