Дифференцирование неявно заданных функций

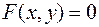Пусть функция задана уравнением . В этом случае говорят, что функция задана неявно. Предположим, что функция дифференцируема. Если в уравнении 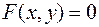под подразумевать функцию , то это уравнение обращается в тождество по аргументу : 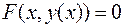. Дифференцируем его по , считая, что есть функция . Получаем новое уравнение, содержащее , и . Разрешая его относительно , находим производную искомой функции , заданной в неявном виде.

Пример. Найти производную функции , заданной неявно.

Решение. Дифференцируя по неявную функцию и считая, что — функция от , имеем ,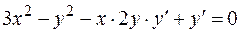

,

.

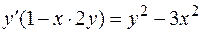Отметим, что в этом случае .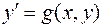

По определению вторая производная от функции есть производная от первой производной. Следовательно, для нахождения второй производной надо продифференцировать найденную первую производную по аргументу , продолжая рассматривать как функцию от . В выражение для второй производной в общем случае войдут , и . Подставляя вместо его значение, находим , зависящую только от и . Аналогично поступаем при нахождении производных более высоких порядков.

Пример. Найти производную второго порядка от функции , за­данной уравнением .

Решение. Найдем первую производную

.

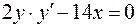
Диф­ференцируя данное уравнение вторично, получаем .

Так как , имеем .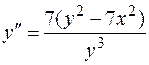

Дата добавления: 2014-01-04