Несобственные интегралы с бесконечными

Несобственные интегралы

Несобственные интегралы являются обобщением определенных интегралов в случаях бесконечных промежутков интегрирования и неограниченных функций.

пределами интегрирования (первого рода)

Пусть функция непрерывна на проме­жутке . Тогда она будет непрерывной на любом конечном от­резке , . Для функции , непрерывной на , сущест­вует определенный интеграл

,

зависящий от верхнего предела интегрирования. Этот интеграл определяет некоторую величину, например площадь криволинейной трапеции, ограниченной графиком функции 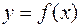r0, прямыми 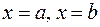и осью 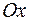. Будем неограни­ченно увеличивать верхний предел интегрирования (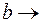+¥). При этом возможны два случая: либо при 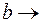+ ¥ имеет предел, либо не имеет.

Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции на промежутке 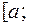+¥)называется предел при +¥:

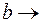(1)

Аналогично определяется несобственный интеграл с бесконечным нижним пределом интегрирования от непрерывной функции на промежутке (–¥: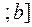

(2)

Если пределы в правых частях формул (1) и (2) существуют и конечны, то соответствующие несобственные интегралы называются сходящимися, если пределы не существуют или бесконечны,— то расходящимися.

Несобственный интеграл с двумя бесконечными пределами интегрирования от непрерывной функции на промежутке ]–¥;+¥[, обозначаемый 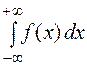, предварительно представляют в виде

,

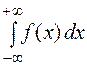
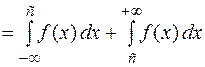Тогда по определению

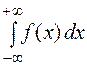
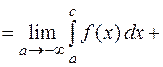
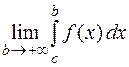(3)

причем этот несобственный интеграл называется сходящимся, если оба предела существуют. Если хотя бы один из пределов не существует или бесконечен, то несобственный интеграл 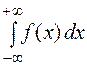называет­ся расходящимся.

Интегралы (1) — (3)называются также несобственными интегралами первого рода.

С геометрической точки зрения сходящийся несобственный ин­теграл 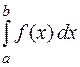означает, что фигура, ограниченная кривой 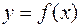r0, прямыми 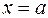, у = 0 и бесконечно вытянутая в направ­лении оси 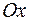, имеет конечную площадь .

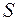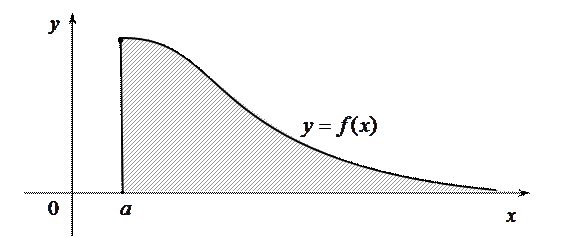
Аналогичная геометрическая интерпретация имеет место для сходящихся несобст­венных интегралов (2) и (3).

Пример. Исследовать на сходимость интеграл .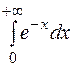

Дата добавления: 2014-01-04