Метод покоординатного спуска

Пусть нужно найти наименьшее значение целевой функции u = f(M) = f(x₁, x₂, …, x_n). Здесь через М обозначена точка n- мерного пространства с координатами x₁, x₂, …, x_n: M = (x₁, x₂, …, x_n). Выберем какую-нибудь начальную точку M₀ = (x₁₀, x₂₀, …, x_n0) и рассмотрим функцию f при фиксированных значениях всех переменных, кроме первой: f(x₁, x₂₀, …, x_n0). Тогда она превратится в функцию одной переменной x₁. Изменяя эту переменную, будем двигаться от начальной точки x₁ = x₁₀ в сторону убывания функции, пока не дойдем до минимума при x₁ = x₁₁, после которого она начинает возрастать. Точку с координатами {x₁₁, x₂₀, x₃₀, …, x_n0} обозначим через M₁, при этом f(M₀) ≥ f(M₁).

Фиксируем теперь переменные x₁ = x₁₁, x₃ = x₃₀, …, x_n = x_n0 и рассмотрим функцию f как функцию одной переменной x₂ : f(x₁₁, x₂, x₃₀, …, x_n0). Изменяя x₂, будем опять двигаться от начального значения x₂ = x₂₀ в сторону убывания функции, пока не дойдем до минимума при x₂ = x₂₁. Точку с координатами {x₁₁, x₂₁, x₃₀, …, x_n0} обозначим через M₂, при этом f(M₁) ≥ f(M₂).

Проведем такую же минимизацию целевой функции по переменным x₃, x₄, …, x_n. Дойдя до переменной x_n, снова вернемся к x₁ и продолжим процесс. Эта процедура вполне оправдывает название метода. С ее помощью мы можем построить последовательность точек M₀, M₁, M₂, …, M_n, которой соответствует монотонная последовательность значений функции f(M₀) ≥ f(M₁) ≥ f(M₂) ≥.... Обрывая ее на некотором шаге k, можно приближенно принять значение функции f(M_k) за ее наименьшее значение в заданной области.

Отметим, что заданный метод сводит задачу поиска наименьшего значения функции нескольких переменных к многократному решению одномерных задач оптимизации. Если целевая функция задана явной формулой и дифференцируема, то мы можем вычислить её частные производные, использовав их для определения направления убывания функции по каждой переменной и поиска соответствующих одномерных минимумов. В противном случае, когда явной формулы для целевой функции нет, одномерный задачи следует решать с помощью методов описанных в подразделе 5.3.

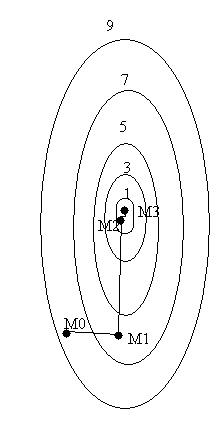
Рисунок 5.5.

На рисунке 5.5 изображены лини уровня некоторой функции двух переменных u=f(x,y) Вдоль этих линий функция сохраняет постоянные значения, равные 1,3,5,7,9. Показана траектория поиска её наименьшего значения, которое достигается в точке О, с помощью метода покоординатного спуска. При этом надо понимать, что рисунок служит только для иллюстрации.

Дата добавления: 2014-01-04