
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Фрактальная размерность. Размерность Хаусдорфа-Безиковича
|
|
|
|
Фракталы сложно рассматривать как множество точек, вложенных в пространство. Когда речь идет об обычных геометрических объектах: линия, поверхность, шар, то их топологические размерности 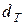 известны и являются целыми числами.
известны и являются целыми числами.
Рассмотрим, как вводится мера некоторого множества точек G, вложенного в пространство при определении размерности Хаусдорфа-Безиковича ( 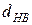 ).
).
Простой способ измерить длину кривых, площадь поверхности или объем тела состоит в том, чтобы разделить их на небольшие элементы – отрезки длиной 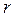 , квадраты со стороной
, квадраты со стороной 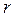 или на небольшие кубы с ребрами
или на небольшие кубы с ребрами 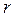 (рис. 3.1). Такой способ, например, применен попугаем в известном м/ф, когда он установил, что длина удава составляет 38 попугаев. С математической точки зрения мы применим некоторую элементарную меру (мерило, величина чего-то), как пробную функцию
(рис. 3.1). Такой способ, например, применен попугаем в известном м/ф, когда он установил, что длина удава составляет 38 попугаев. С математической точки зрения мы применим некоторую элементарную меру (мерило, величина чего-то), как пробную функцию  , где
, где 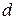 – размерность меры.
– размерность меры.
Пусть для некоторой кривой 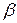 (рис. 2.1) длиной Lo, получено N(r) прямолинейных отрезков длиной
(рис. 2.1) длиной Lo, получено N(r) прямолинейных отрезков длиной 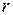 , аппроксимирующих данную кривую. Тогда, если
, аппроксимирующих данную кривую. Тогда, если 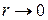 , получим:
, получим:
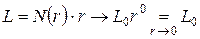 . (2.1)
. (2.1)
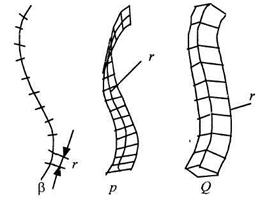
Рисунок 2.1 – Измерение «величины» различных множеств точек с помощью отрезков, квадратов и кубов с ребрами 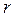 .
.
В пределе при 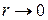 мера L становится равной длине кривой
мера L становится равной длине кривой 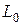 и не зависит от
и не зависит от 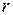 .
.
Множеству точек кривой 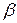 можно поставить в соответствие и площадь. Если N(r) – число квадратов,
можно поставить в соответствие и площадь. Если N(r) – число квадратов,  – площадь каждого из них, то площадь кривой
– площадь каждого из них, то площадь кривой 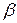 определяется как:
определяется как:
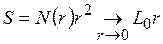 . (2.2)
. (2.2)
Аналогично, объем V кривой 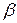 может быть найден как:
может быть найден как:
 . (2.3)
. (2.3)
Разумеется, что для обычных кривых 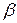 площадь
площадь 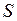 и объем V обращаются в нули при
и объем V обращаются в нули при 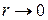 и тогда единственной (представляющей интерес) мерой является длина кривой L.
и тогда единственной (представляющей интерес) мерой является длина кривой L.
Теперь перейдем к поверхности 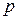 (рис. 2.1), для которой в качестве меры множества точек возьмем площадь:
(рис. 2.1), для которой в качестве меры множества точек возьмем площадь:
|
|
|
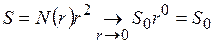 . (2.4)
. (2.4)
Можно ли для поверхности 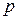 в качестве меры взять объем? Формально это выглядит следующим образом:
в качестве меры взять объем? Формально это выглядит следующим образом:
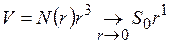 . (2.5)
. (2.5)
При 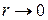 этот объем для обычной поверхности также равен нулю.
этот объем для обычной поверхности также равен нулю.
Поставим другой вопрос: можно ли поверхности 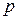 поставить в соответствие какую-нибудь длину?
поставить в соответствие какую-нибудь длину?
Формально мы можем принять за такую длину величину:
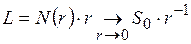 , (2.6)
, (2.6)
которая расходится при 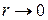 .
.
Этот результат объясняет, что поверхность невозможно покрыть конечным числом прямолинейных отрезков.
Вывод: единственной мерой множества точек, образующих поверхность в трехмерном пространстве является площадь.
Однако существуют «монстры», подобные кривой Пеано, «снежинке Коха» и другие, для которых требуется обобщить меру величины множества точек.
До сих пор, определяя меру величины множества точек G в пространстве, мы выбирали некоторую элементарную меру (пробную функцию) 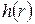 . Введем для пробной функции некоторый геометрический коэффициент y(d), зависящий от пробной функции:
. Введем для пробной функции некоторый геометрический коэффициент y(d), зависящий от пробной функции:
 , (2.7)
, (2.7)
Для прямолинейных отрезков, квадратов, кубов геометрический коэффициент принимается равным 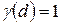 , однако для других геометрических объектов он будет иным. Так, например, для круга
, однако для других геометрических объектов он будет иным. Так, например, для круга  , для сферы
, для сферы 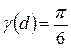 .
.
После выбора пробной функции 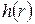 множество G покрывается N(r) пробными функциями (элементарными мерами) и определяется мера этого множества:
множество G покрывается N(r) пробными функциями (элементарными мерами) и определяется мера этого множества:
 . (2.8)
. (2.8)
Анализируя это выражение, можно сделать вывод, что при 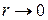 мера
мера 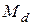 равна бесконечности (при
равна бесконечности (при 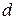 =0 получаем
=0 получаем 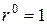 и
и 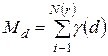 или нулю (при некоторой величине
или нулю (при некоторой величине 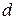 малая величина
малая величина 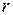 приближается к нулю). Отсюда следует вывод, что моменту перехода
приближается к нулю). Отсюда следует вывод, что моменту перехода 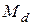 из нуля в бесконечность соответствует некоторое конечное значение
из нуля в бесконечность соответствует некоторое конечное значение 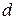 .
.
Размерность Хаусдорфа-Безиковича 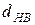 множества точек G есть критическая размерность, при которой мера
множества точек G есть критическая размерность, при которой мера 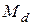 изменяет свое значение с нуля на бесконечность:
изменяет свое значение с нуля на бесконечность:
 . (2.9)
. (2.9)
Приняв y(d) = 1, то есть, покрыв множество точек прямолинейными объектами (отрезок, квадрат, куб) и приравняв 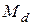 некоторой конечной величине, например 1, получим:
некоторой конечной величине, например 1, получим:
|
|
|
 , (2.10)
, (2.10)
откуда размерность Хаусдорфа-Безиковича определим по формуле:
 . (2.11)
. (2.11)
Если 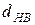 является дробной, то размерность Хаусдорфа-Безиковича будем обозначать
является дробной, то размерность Хаусдорфа-Безиковича будем обозначать 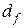 и называть фрактальной размерностью Хаусдорфа-Безиковича.
и называть фрактальной размерностью Хаусдорфа-Безиковича.
Теперь перейдем к построению и изучению самоподобных фракталов.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2178; Нарушение авторских прав?; Мы поможем в написании вашей работы!