Элементарные катастрофы

ВВЕДЕНИЕ В ТЕОРИЮ КАТАСТРОФ

Теория катастроф родилась на стыке двух дисциплин – топологии и математического анализа. Её источниками являются теория особенностей гладких отображений Х. Уитни, а также теория устойчивости и бифуркаций динамических систем А. Пуанкаре, А. Ляпунова, А. Андронова. Оба эти направления слились, благодаря усилиям французского математика Р. Тома, в единую теорию, которая получила название – теория катастроф.

При изучении свойств решений дифференциальных уравнений сначала необходимо явно оценить полное множество решений и лишь потом анализировать их свойства. Проблем не возникает, если это линейная, лучше стационарная система дифференциальных уравнений. Для нелинейных систем полное множество решений можно построить для уравнений второго порядка (например, методом фазовой плоскости). Что же касается уравнений третьего и более высокого порядка, то здесь известны решения только частных задач. Как же поступать в этом случае?

Анри Пуанкаре убедительно показал, что во многих случаях необходим лишь ограниченный объем информации качественного характера, которая, в конечном итоге, и представляет интерес при изучении конкретных динамических систем.

Основы современного подхода к определению качественных изменений в поведении решений обыкновенных дифференциальных уравнений были заложены А. Пуанкаpe в конце 19 века. Он впервые ввел такие понятия, как структурная устойчивость, динамическая устойчивость и критические множества. Пуанкаре исследовал качественное изменение поведения динамической системы при изменении описывающих ее параметров.

Перестройка качественной картины движения динамической системы при изменении ее параметров получила название бифуркации (буквально, раздвоение).

Таким образом, предмет теории катастроф – изучение зависимости качественной природы решений уравнений от значений параметров, присутствующих в заданных уравнениях.

Теория катастроф анализирует критические точки (репетиции) потенциальной функции, то есть точки, где не только первая производная функции равна нулю, но и равны нулю же производные более высокого порядка. Динамика развития таких точек может быть изучена при помощи разложения потенциальной функции в рядах Тейлора посредством малых изменений входных параметров. Если точки роста складываются не просто в случайный узор, но формируют структурированную область стабильности, эти точки существуют как организующие центры для особых геометрических структур с низким уровнем вырожденности и с высоким уровнем катастрофичности в окружающих их областях фазового пространства. Если потенциальная функция зависит от трёх или меньшего числа активных переменных, и пяти или менее активных параметров, то в этом случае существует всего семь обобщённых структур описанных геометрий бифуркаций, которым можно приписать стандартные формы разложений в ряды Тейлора). Сегодня эти семь фундаментальных типов катастроф известны под именами, которые им дал Рене Том:

Катастрофа типа «Складка».

Катастрофа типа «Сборка».

Катастрофа типа «Ласточкин хвост».

Катастрофа типа «Бабочка».

Гиперболическая омбилика.

Эллиптическая омбилика.

Параболическая омбилика.

Первые два типа встречаются наиболее часто, остальные встречаются реже в специфических областях (трехмерные объекты, оптика, исследования волн и т.п.).

Катастрофа типа «Складка»

Катастрофа складки задается функцией, зависящей от одного управляющего параметра:

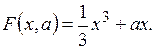(4.1)

График катастрофы складки представлен на рисунке 4.1,а.

В точке (0,0) функция имеет перегиб. При возмущении функции F(x,a) управляющим параметром а получим два возможных состояния системы:

- при а>0 функция не имеет критических точек (система устойчива);

- при а<0 функция имеет две критические точки (система неустойчива):

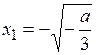, . (4.2)

Вырожденная критическая точка х = 0 функции F(x,a) рассыпается на две невырожденные под действием возмущения a <0. В этом состоит неустойчивость катастрофы складки.

Критические и вырожденные точки этого семейства находятся из условия равенства нулю первой и второй производных функции F(x,a) по х.

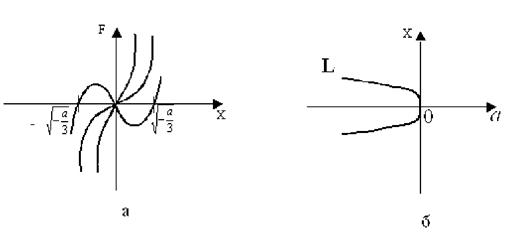
Рисунок 4.1 – Геометрия катастрофы типа «складка»

При этом получаются уравнения:

(4.3)

Кривая равновесия L (рис. 4.1,б) катастрофы складки представляет собой множество точек (х,а) на плоскости 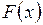, удовлетворяющих уравнению (4.3). Верхняя часть параболы отвечает точкам локального минимума, а нижняя - точкам локального максимума функций.

Катастрофа типа «Сборка»

Катастрофа сборки может быть представлена в виде структуры критических точек семейства функций (рис. 4.2,а)

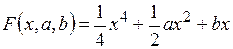. (4.4)

где х – переменное состояние системы; a, b — управляющие параметры.

Критические вырожденные точки семейства F находятся из условия равенства нулю первой второй и третьей производных F, соответственно:

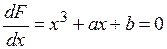; (4.5)

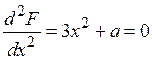; (4.6)

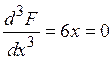. (4.7)

Из (4.6) можно найти сечение катастрофы сборки в плоскости (х,а), которое представляет собой параболу (рис. 4.2,г):

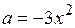. (4.8)

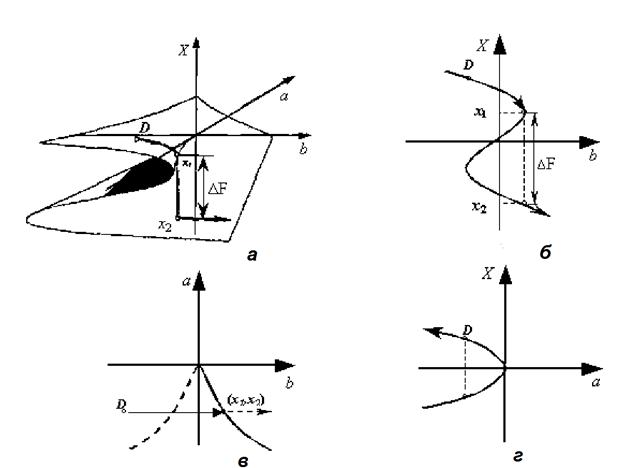
Рисунок 4.2 – Геометрия катастрофы типа «сборка»

Подставим (4.8) в (4.5), получим сечение катастрофы сборки в плоскости (х, b), показанное на рисунке 4.2,б.

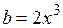. (4.9)

Решая систему уравнений (4.8) и (4.9) относительно х получаем бифуркационное множество (рис. 4.2,в):

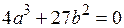. (4.10)

Бифуркационное множество это множество точек поверхности, обладающие двойственностью функции. Это множество определяет область неустойчивости системы.

Когда параметры системы (точка D на рис. 4.2), плавно изменяясь, пересекают бифуркационное множество, то система скачком переходит из одного состояния устойчивого равновесия 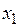в другое –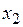

Стохастический характер причинности и бифуркационные механизмы ведут к широкому многообразию различных форм организации живой, неживой материи и общества. Это приводит к росту сложности системы. Таким образом, процесс самоорганизации ведет к непрерывному росту организационных форм.

Дата добавления: 2014-01-04