Общая постановка задачи динамического программирования

Задачи динамического программирования

Рис. 6.6. Дерево задач

Рис. 6.5. Решение задачи (1.2.2)

Рис. 6.4. Решение задачи (1.2.1)

Оптимальное решение 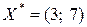удовлетворяет условию целочисленности исходной задачи. Для рассматриваемой задачи 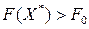(27 > 26), то .

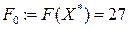Решим задачу (1.2.2):

Задача (1.2.2) не имеет решения, вычеркиваем ее из общего списка.

Список задач исчерпан, о чем свидетельствует дерево задач (рис. 6.6).

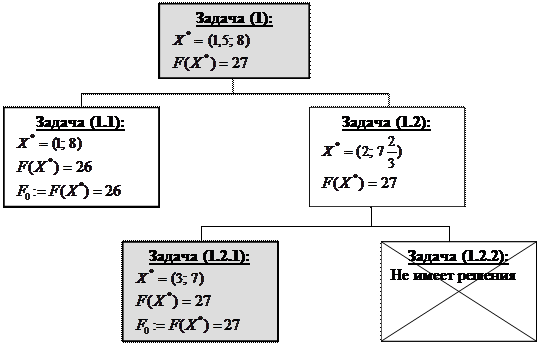Оптимальное целочисленное решение задачи (1.2.1) обеспечивает большее значение целевой функции, чем оптимальное целочисленное решение задачи (1.1), следовательно, его принимаем в качестве оптимального для исходной целочисленной задачи.

Ответ: оптимальное целочисленное решение: , .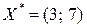

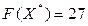Динамическое программирование – метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми.

Начало развития динамического программирования относится к 50-м годам ХХ в. и связано с именем Ричарда Эрнеста Беллмана.

Если модели линейного программирования можно использовать в экономике для принятия крупномасштабных плановых решений в сложных ситуациях, то модели динамического программирования применяются при решении задач значительно меньшего масштаба, например, при разработке правил управления запасами; при распределении инвестиционных ресурсов между альтернативными проектами; при составлении календарных планов текущего и капитального ремонта сложного оборудования и его замены и т.п.

Общая постановка задачи динамического программирования.

Рассматривается управляемый процесс, например, процесс распределения средств между предприятиями, использования ресурсов в течение ряда лет, замены оборудования и т.п. В результате управления система (объект управления) S переводится из начального состояния s₀ в состояние s_n. Пусть, управление можно разбить на n шагов, т.е. решение принимается последовательно на каждом шаге, а управление, переводящее систему S из начального состояния в конечное, представляет собой совокупность n пошаговых управленческих решений.

Обозначим через X_k управленческое решение на k -м шаге (k =1, 2, …, n). Переменные X_k удовлетворяют некоторым ограничениям и в этом смысле называются допустимыми (X_k может быть числом, точкой в n -мерном пространстве или качественным признаком).

Пусть X= (X₁, X₂, …, X_n) – управление, переводящее систему S из состояния s₀ в состояние s_n. Обозначим через s_k состояние системы (характеризуемое определенным набором параметров и конкретных их значений) после k -го шага управления. Причем состояние системы s_k в конце k -го шага зависит только от предшествующего состояния s_k-1 и управленческого решения на k -ом шаге X_k (т.е. не зависит напрямую от предшествующих состояний и управленческих решений). Данное требование называется «отсутствием последствия» и может быть выражено следующими уравнениями состояний:

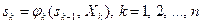. (11.1)

Таким образом, получаем последовательность состояний s₀, s₁, …, s_k-1, s_k, …, s_n-1, s_n. Тогда n -шаговый управленческий процесс схематично можно изобразить следующим образом:

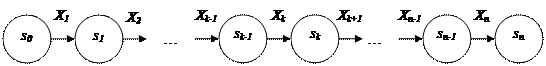Пусть показатель эффективности k -го шага выражается некоторой функцией:

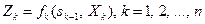, (11.2)

а эффективность всего рассматриваемого многошагового процесса следующей аддитивной функцией:

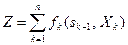, (11.3)

или

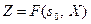. (11.4)

Тогда задача пошаговой оптимизации (задача динамического программирования) формулируется следующим образом: определить такое допустимое управление Х, переводящее систему S из состояния s₀ в состояние s_n, при котором целевая функция Z принимает наибольшее (наименьшее) значение.

Задача динамического программирования обладает следующими особенностями:

1. Задача оптимизации интерпретируется как n -шаговый процесс управления.

2. Целевая функция равна сумме целевых функций каждого шага.

3. Выбор управления на k -ом шаге зависит только от состояния системы к этому шагу, не влияет на предшествующие шаги (отсутствие обратной связи).

4. Состояние s_k после k -го шага управления зависит только от предшествующего состояния s_k-1 и управления X_k («отсутствие последствия»).

5. На каждом шаге управление X_k зависит от конечного числа управляющих переменных, а состояние s_k – от конечного числа параметров.

Дата добавления: 2013-12-12