
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Законы алгебры высказываний
|
|
|
|
Операции над высказываниями
Основные понятия
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
ЛЕКЦИЯ №3
Контрольные вопросы
1. Запишите ассоциативный, дистрибутивный и коммутативный законы операций над множествами. 2. Свойства идемпотентности операций объединения и пересечения. 3. Законы де Моргана. 4. Какие числа называются натуральными? 5. Позиционная и непозиционная система счисления. 6. Какие числа называются целыми? 7. Рациональные числа. 8. Какие числа называются иррациональными? 9. Алгебраические числа и трансцендентные. 10. Действительные числа. 11. Комплексные числа.
План
1. Основные понятия
2. Операции над высказываниями
3. Законы алгебры высказываний
4. Строение математической теоремы
Математическая логика – современный вид формальной логики, изучающей правила выведения следствий из различных посылок, истинность которых очевидна. Математическая логика возникла в середине XIX в для потребностей математики и стала применяться в самых различных областях знаний, в том числе и в правоприменительной деятельности.
Появление математической логики математики связывают с Джорджем Булем (1815-1864), с его работами «Математический анализ логики» (1847), «Логическое исчисление» (1848) и «Законы мысли» (1854). В этих работах было показано, что законы формальной логики, представленные в виде кодов еще Аристотелем, сами могут быть предметом исчисления. Это были первые работы, объединяющие логику и математику. В 40-50-х гг. ХX века математическая логика получила особенное значение в связи с развитием вычислительной техники.
Математическая логика исследует законы логических процессов, применяя математические методы.
|
|
|
Основным понятием математической логики является понятие высказывания (высказывания будем обозначать латинскими буквами: 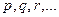 ).
).
Определение 3.1. Высказыванием называется повествовательное предложение естественного языка, о котором имеет смысл говорить истинно оно или ложно.
Пример 3.1. «Москва – столица России» – истинное высказывание.
2х5=43 – ложное высказывание.
5>10 – ложное высказывание.
Какая сегодня погода? – не является высказыванием, т.к. здесь ничего не утверждается.
Пример 3.2. 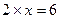 . При
. При 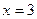 – высказывание истинное, при
– высказывание истинное, при 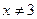 – ложное.
– ложное.
Пример 3.3. «Река 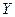 впадает в Каспийское море». Если в таком предложении вместо
впадает в Каспийское море». Если в таком предложении вместо 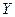 вписать название конкретной реки, то получим высказывание, которое будет ложно или истинно. Высказывание «Река Волга впадает в Каспийское море» является истинным.
вписать название конкретной реки, то получим высказывание, которое будет ложно или истинно. Высказывание «Река Волга впадает в Каспийское море» является истинным.
Такого рода высказывания, когда в зависимости от неизвестного параметра оно может быть или истинным или ложным также называют предикатами. Предикаты обозначаются прописными буквами латинского алфавита: 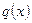 ,
, 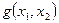 и т.п.
и т.п.
Определение 3.2. Функция 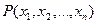 , определенная на некотором множестве X и принимающая одно из двух значений: истина или ложь называется n – мерным предикатом.
, определенная на некотором множестве X и принимающая одно из двух значений: истина или ложь называется n – мерным предикатом.
Рассматриваемые высказывания – нуль мерные предикаты. Поэтому логика предикатов, как частный случай, включает в себя логику высказываний.
Множество истинности неопределенных высказываний (предикатов) будем обозначать прописными буквами: 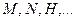 .
.
Пример 3.4. Для следующего неопределенного высказывания 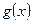 :
: 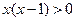 найдем множество истинности. Решив неравенство, получим:
найдем множество истинности. Решив неравенство, получим: 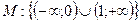 .
.
Имеются неопределенные высказывания 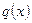 и
и 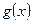 . Оба они определены на одном и том же множестве. Они являются равносильными, если множество истинности первого высказывания
. Оба они определены на одном и том же множестве. Они являются равносильными, если множество истинности первого высказывания 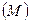 совпадает со множеством истинности второго
совпадает со множеством истинности второго 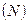 , т.е.
, т.е. 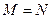 .
.
Пример 3.5. Равносильными будут следующие предикаты: 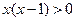 и
и 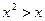 .
.
Каждому логическому высказыванию поставим в соответствие численное значение: 1 – если высказывание истинно, 0 – если высказывание ложное. Рассматривая высказывания как величины, принимающие значения 1 и 0, можно определить над ними операции, которые позволяют получать новые высказывания из данных. Эти операции будут выражать логические связи, употребляемые в обычной речи, например: не, и, или, если - то, тогда и только тогда и т.д.
|
|
|
Операции, производимые над высказываниями, называются логическими операциями. Совокупность логических операций получила название алгебры высказываний.
Определение 3.3. Отрицанием высказывания  называется высказывание, истинное тогда и только тогда, когда p ложно. Отрицание обозначается
называется высказывание, истинное тогда и только тогда, когда p ложно. Отрицание обозначается 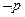 или
или  и читается «не
и читается «не  ».
».
В естественном языке отрицание соответствует составлению из высказывания p нового высказывания «неверно, что  », или «не
», или «не  ».
».
Соотношение между  ,
, 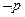 можно определить, воспользовавшись диаграммой Эйлера-Венна (рис. 3.1).
можно определить, воспользовавшись диаграммой Эйлера-Венна (рис. 3.1).
Составим таблицу истинности операции отрицания.
Отрицание истинного высказывания является ложным высказыванием, отрицание ложного – истинное высказывание. Двойное отрицание обозначается 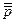 .
.
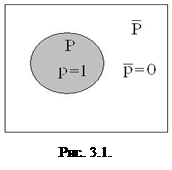
Таблица 3.1
Таблица истинности
отрицания

| 
|
Пример 3.5. Для высказывания «Река Волхов вытекает из озера Ильмень» отрицанием будет высказывание «Неверно, что река Волхов вытекает из озера Ильмень» или «Река Волхов не вытекает из озера Ильмень», а двойным отрицанием будет высказывание «Неверно, что река Волхов не вытекает из озера Ильмень».
Определение 3.3. Конъюнкцией двух высказываний  и
и  называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания. Конъюнкция высказываний обозначается
называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания. Конъюнкция высказываний обозначается 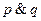 ,
, 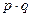 или
или 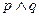 и читается «
и читается « и
и  ».
».
В естественном языке конъюнкция соответствует соединению высказываний союзом «и».
Составим таблицу истинности операции конъюнкции. Множество истинности для конъюнкции между  и
и  можно определить., воспользовавшись диаграммой Эйлера – Венна (рис. 3.2). Для этого определим:
можно определить., воспользовавшись диаграммой Эйлера – Венна (рис. 3.2). Для этого определим: 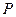 – множество истинности для высказывания
– множество истинности для высказывания  , Q - множество истинности для высказывания
, Q - множество истинности для высказывания  . Множество истинности для высказывания
. Множество истинности для высказывания 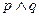 является множество
является множество 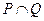 . Оно представлено на диаграмме закрашенной областью.
. Оно представлено на диаграмме закрашенной областью.
|
|
|
Таблица 3.2
Таблица истинности
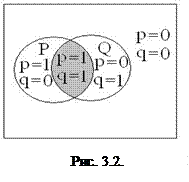 конъюнкции
конъюнкции

| 
| 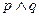
|
Пример 3.6. Для высказываний «8 делится на 2», «8 делится на 4» их конъюнкцией будет высказывание «8 делится на 2 и 4», которое, очевидно, будет истинным.
Определение 3.4. Дизъюнкцией двух высказываний  и
и  называется высказывание ложное тогда и только тогда, когда ложны оба эти высказывания. Дизъюнкция высказываний
называется высказывание ложное тогда и только тогда, когда ложны оба эти высказывания. Дизъюнкция высказываний  и
и  обозначается
обозначается 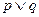 или
или 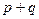 и читается «
и читается « или
или  » (в неразделительном смысле).
» (в неразделительном смысле).
В естественном языке дизъюнкция соответствует соединению высказываний союзом «или» в неразделительном смысле.
Составим таблицу истинности операции дизъюнкции. Множество истинности для дизъюнкции между  и
и  можно определить, воспользовавшись диаграммой Эйлера – Венна (аналогично конъюнкции) (рис. 3.3).
можно определить, воспользовавшись диаграммой Эйлера – Венна (аналогично конъюнкции) (рис. 3.3).
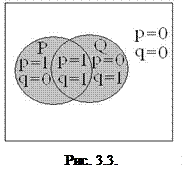 Таблица 3.3
Таблица 3.3
Таблица истинности
дизъюнкции

| 
| 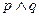
|
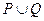 – множество истинности для высказывания
– множество истинности для высказывания 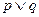 (на диаграмме – закрашенная область).
(на диаграмме – закрашенная область).
Пример 3.7. Высказывание «В треугольнике 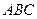 угол
угол  или
или 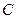 – острый» истинно, так как обязательно истинно хотя бы одно из высказываний. «В треугольнике
– острый» истинно, так как обязательно истинно хотя бы одно из высказываний. «В треугольнике 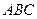 угол
угол  острый», «В треугольнике
острый», «В треугольнике 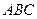 угол
угол 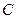 острый».
острый».
Определение 3.5. Импликацией двух высказываний  и
и  называется высказывание ложное тогда и только тогда, когда
называется высказывание ложное тогда и только тогда, когда  истинно, а
истинно, а  ложно.
ложно.
Импликация высказываний обозначается 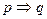 , или
, или 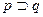 и читается: «
и читается: « влечет
влечет  », или «если
», или «если  , то
, то  », или «из
», или «из  следует
следует  », или «
», или « является достаточным для
является достаточным для  », или «
», или « является необходимым условием для
является необходимым условием для  ».
».
Высказывание  называется посылкой импликации, а
называется посылкой импликации, а  – заключением.
– заключением.
Термин «импликация» происходит от латинского implicate – тесно связываю.
Составим таблицу для операции импликация.
Таблица 3.4
Таблица истинности импликации

| 
| 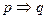
|
Пример 3.8. Сравним такие предложения: «Если число  делится на 4, то оно делится на 2»; «Если Сидоров увлечен математикой, то Смирнов ничем, кроме футбола, не интересуется». Очевидно, что смысл союза «если... то...» в этих предложениях не один и тот же. В первом случае он соответствует импликации. Второе предложение не является высказыванием.
делится на 4, то оно делится на 2»; «Если Сидоров увлечен математикой, то Смирнов ничем, кроме футбола, не интересуется». Очевидно, что смысл союза «если... то...» в этих предложениях не один и тот же. В первом случае он соответствует импликации. Второе предложение не является высказыванием.
|
|
|
Пример 3.9. Предположим, вы работаете в юридической консультации, к вам приходит глава разорившейся фирмы (но некогда процветавшей). Фирма производила какую-то продукцию. Глава фирмы издал распоряжение следующего содержания: «Если будет улучшено качество продукции, то все получат премию», а сам улетел отдыхать на Канарские острова на месяц. По возвращении выясняется, что повышения качества не было, но управляющий премию выплатил, т.к. деньги были. Вскоре фирма разорилась (деньги предназначены были для закупки сырья материалов). Глава фирмы теперь собирается через суд взыскать большую сумму денег для компенсации потерь с управляющего, который, по мнению хозяина, исказил его распоряжение.
Эта ситуация соответствует третьей строке таблицы истинности импликации. Повышения качества продукции не было (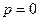 ), а премия была вы плачена (
), а премия была вы плачена (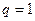 ). По логическому значению импликации управляющий поступил правильно. Впрочем, если бы он не выдал премию, то также не нарушил бы правило импликации.
). По логическому значению импликации управляющий поступил правильно. Впрочем, если бы он не выдал премию, то также не нарушил бы правило импликации.
Определение импликации вынуждает считать истинными высказываниями такие предложения, как «Если 2+2=5, то Москва – столица России» или «Если 2-2=3, то существуют летающие зайцы». Эти предложения, вероятно, кажутся бессмысленными. Дело в том, что мы привыкли соединять союзом «если... то» (также как и другими союзами) предложения, связанные по смыслу. Но определениями логических операций смысл составляющих высказываний никак не учитывается; они рассматриваются как объекты, обладающие единственным свойством – быть истинными либо ложными. Поэтому не следует смущаться «бессмысленностью» некоторых составных высказываний. Их смысл не входит в предмет нашего рассмотрения.
Определение 3.6. Эквивалентностью двух высказываний  и
и  называется высказывание истинное тогда и только тогда, когда истинности
называется высказывание истинное тогда и только тогда, когда истинности  и
и  совпадают.
совпадают.
Эквивалентность обозначается 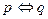 или
или 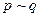 и читается «
и читается « эквивалентно
эквивалентно  », или «
», или « тогда и только тогда, когда
тогда и только тогда, когда  », или «
», или « является необходимым и достаточным для
является необходимым и достаточным для  ».
».
Составим таблицу для операции эквивалентность.
Таблица 3.5
Таблица истинности эквивалентности

| 
| 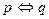
|
Пример 3.9. Высказывание «Треугольник 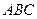 с вершиной
с вершиной 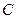 и основанием
и основанием 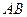 равнобедренный тогда и только тогда, когда
равнобедренный тогда и только тогда, когда 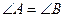 » является истинной, так как высказывания «Треугольник
» является истинной, так как высказывания «Треугольник 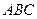 с вершиной
с вершиной 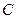 и основанием
и основанием 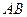 равнобедренный» и «В треугольнике
равнобедренный» и «В треугольнике 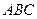 с вершиной
с вершиной 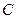 и основанием
и основанием 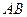
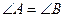 » либо одновременно истинны, либо одновременно ложны.
» либо одновременно истинны, либо одновременно ложны.
Эквивалентность играет важную роль в математических доказательствах.
Логические связки позволяют из простых высказываний получить новые, сколь угодно сложные высказывания. Рассмотрим пример: «Если завтра будет дождь или снег, то я возьму зонт и надену пальто или свитер». Введем обозначения:  = «Завтра будет дождь»;
= «Завтра будет дождь»; 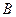 = «Завтра будет снег»;
= «Завтра будет снег»; 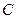 = «Я возьму зонт»;
= «Я возьму зонт»; 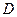 = «Я надену пальто»;
= «Я надену пальто»; 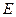 = «Я надену свитер». Тогда наше предложение можно записать в виде:
= «Я надену свитер». Тогда наше предложение можно записать в виде:
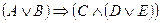 .
.
Рассмотренная процедура называется формализацией. При переводе на язык логики первоначальный смысл предложений не воспроизводится, а, напротив, почти полностью игнорируется; зато их структура сохраняется и становится явной, четко и однозначно выраженной.
Первые три закона сформулированы еще Аристотелем.
1. 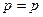 – закон тождества (мысль, заключенная в некотором высказывании, остается неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует).
– закон тождества (мысль, заключенная в некотором высказывании, остается неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует).
2. 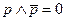 – закон противоречия (никакое предложение не может быть истинным одновременно со своим отрицанием).
– закон противоречия (никакое предложение не может быть истинным одновременно со своим отрицанием).
3. 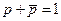 – закон исключения третьего (для каждого высказывания имеются лишь две возможности: это высказывание или истинно или ложно, третьего не дано).
– закон исключения третьего (для каждого высказывания имеются лишь две возможности: это высказывание или истинно или ложно, третьего не дано).
4. 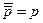 – закон двойного отрицания.
– закон двойного отрицания.
5. 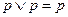 – идемпотентность операции дизъюнкции.
– идемпотентность операции дизъюнкции.
6. 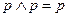 – идемпотентность операции конъюнкции.
– идемпотентность операции конъюнкции.
7. 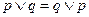 – коммутативность операции дизъюнкции.
– коммутативность операции дизъюнкции.
8. 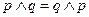 – коммутативность операции конъюнкции.
– коммутативность операции конъюнкции.
9. 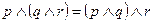 – ассоциативность операции конъюнкции.
– ассоциативность операции конъюнкции.
10. 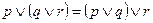 – ассоциативность операции дизъюнкции.
– ассоциативность операции дизъюнкции.
11. 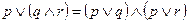 – дистрибутивность операции дизъюнкции относительно конъюнкции.
– дистрибутивность операции дизъюнкции относительно конъюнкции.
12. 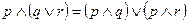 – дистрибутивность операции конъюнкции относительно дизъюнкции.
– дистрибутивность операции конъюнкции относительно дизъюнкции.
13. 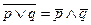 ,
, 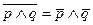 – законы де Моргана для операций дизъюнкция и конъюнкция.
– законы де Моргана для операций дизъюнкция и конъюнкция.
Тождества:
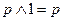 ,
, 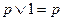 ,
, 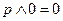 ,
, 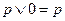 .
.
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 2783; Нарушение авторских прав?; Мы поможем в написании вашей работы!