
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сложение колебанийодного направления
Глава 1. Кинематика
Лекционный блок
1.1. Основные понятия
· Механика – раздел физики, изучающий закономерности механического движения тел и причины, вызывающие (или изменяющие) его.
· Механическоедвижение – процесс изменения с течением времени взаимного расположения тел или частей тела относительно друг друга.
· Кинематика – раздел физики, изучающий механическое движение тел, безотносительно к причинам, вызывающим это движение.
· Классическая (нерелятивистская) механика или механикаНьютона – нерелятивистская теория движения макроскопических объектов.
· Нерелятивистскаятеория –теория движения тел со скоростями V, гораздо меньшими скорости света с: V<<с.
· Основнаязадачакинематики (механики) состоит в определении положения и скорости движущейся материальной точки (тела) в произвольный момент времени.
· Материальнаяточка – модель реального тела:
1) размеры которого стремятся к нулю, говорят: материальная точка не имеет размеров,
2) имеет не равную нулю массу.
В конкретной задаче материальной точкой можно считать тело, размеры которого много меньше, чем расстояния между телами, или размеров области, в которой происходит движение.
· Абсолютнотвердоетело – тело, расстояние между любыми точками которого всегда остается неизменным. Такое тело не способно деформироваться, но под действием внешних сил в нем могут возникать внутренние напряжения, силы упругости и давления.
· Поступательнымдвижением называют движение, при котором любая прямая, проведенная в теле остается параллельной сама себе.
Для указания положения материальной точки в пространстве и описания изменения этого положения во времени вводят систему отсчета.
· Системаотсчета – совокупность: 1) тела отсчета (тела, по отношению к которому определяется положение некоторой материальной точки); 2) системы координат с началом отсчета в точке, выбранной на теле отсчета, 3) часов – прибора для отсчета времени. Можно говорить, что система отсчета представляет собой систему координат, жестко связанную с телом отсчета и часы.
· Радиус - вектор r материальной точки – это вектор, проведенный из начала координат системы отсчета к этой материальной точке.
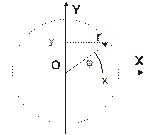
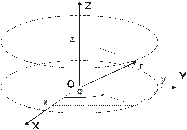
Наиболее часто при решении задач на плоскости вводят декартовы прямоугольные координаты (x, y) и полярные координаты (r, φ); в трехмерном пространстве – декартовы прямоугольные (x, y, z), цилиндрические (z, r, φ) и сферические (r, Θ, φ) системы координат. В декартовой системе координат координаты (x, y, z) материальной точки М определяют как проекции радиус-вектора r этой точки на соответствующие оси системы координат. Взаимосвязь названных систем координат иллюстрируют приведенные ниже рисунки.
|
Рис.1.1а.
Декартовы x,y и и полярные r, j, координаты
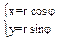
|
|
Рис.1.1b.
Соответствие декартовых x,y,z и и цилиндрических r, j, z координат
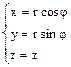
|

| Рис.1.1с.
Соответствие декартовых x,y,z и сферических r, q, f координат
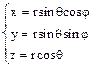
|
Движение материальной точки в пространстве сопровождается изменением ее координат (и ее радиус-вектора) с течением времени. Процесс движения может быть описан системой уравнений, представляющей собой параметрическое уравнениетраектории:
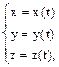
или уравнением для радиус-вектора:
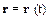 ,
,
где радиус вектор r =(x,y,z).
· Траектория материальной точки может быть определена следующими способами:
1) линия, вдоль которой движется материальная точка (центр масс материального тела) в данной системе отсчета,
2) геометрическое место концов радиус-векторов материальной точки.
Уравнение траектории в явном виде, как уравнение, связывающее между собой пространственные координаты движущейся материальной точки, может быть получено исключением времени из системы уравнений (1.1).
· Путь (длинапути) – скалярная величина численно равная длине участка траектории, пройденного материальной точкой от начального положения С до конечного В (см. рис. 1.2).
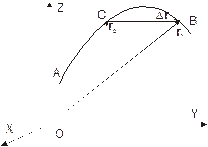
| Рис. 1.2. АСВ - траектория движения материальной точки, r0 и r – ее начальный и конечный радиус-векторы, Dr=S – вектор перемещения |
· Перемещение – вектор S направленный из начального положения движущейся материальной точки в ее конечное положение.
Вектор перемещения S можно определить как приращение D r радиус-вектора материальной точки: S =D r = r 1 – r 0. Рисунок 1.2 позволяет сделать вывод, что модуль вектора перемещения совпадает с длиной пройденного пути лишь при прямолинейном движении.
1.2. Скорость и ускорение
Изменение положения материальной точки в пространстве с течением времени характеризуют с помощью скорости. В физике используется понятие "скорость" используется в нескольких различных смыслах.
· Средняяскоростьдвижения – векторная величина, равная отношению вектора перемещения материальной точки S= D r ко времени Dt, за которое это перемещение произошло:
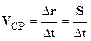
Формальное, количественное определение каждой новой физической величины требует установления ее физического смысла, позволяющего с той или иной степенью наглядности представить конкретную ситуацию. Физический смысл величин устанавливается по определенной схеме. Так, если в формуле (1.3) для средней скорости положить Dt=1 с, то она принимает вид: 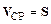 . Поэтому, средняя скорость показывает, какое перемещение совершает материальная точка за единицу времени. Последнее равенство указывает также, что вектор средней скорости V CP направлен вдоль вектора перемещения S.
. Поэтому, средняя скорость показывает, какое перемещение совершает материальная точка за единицу времени. Последнее равенство указывает также, что вектор средней скорости V CP направлен вдоль вектора перемещения S.
Соотношение (1.3) позволяет установить размерность единицы измерения скорости. Для этого в определение величины подставляют (не обращая внимания на векторный характер записи) размерность всех входящих величин:
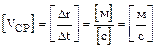 .
.
· Единицаскорости – 1 м/с – есть скорость такого движения, при котором материальная точка за одну секунду проходит расстояние в 1 метр.
· Мгновеннаяскорость – скорость материальной точки в данный момент времени, в данной точке траектории.
Количественное определение мгновенной скорости V требует дополнительных рассуждений. Средняя скорость, характеризует движение в целом, и не является его детальной характеристикой. Мгновенную скорость можно определить путем предельного перехода в соотношении (1.3) при Dt®0:
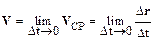 .
.
Из курса математического анализа известно, что такой предел представляет собой первую производную радиус-вектора r по времени t:
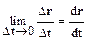 .
.
Таким образом:
· Мгновеннаяскорость – векторная физическая величина, равная первой производной радиус-вектора r материальной точки по времени:
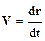
Из приведенных определений следует, что в общем случае вектор средней скорости V CP направлен вдоль перемещения S =D r, т. е. вдоль секущей – линии, проходящей через начальное и конечное положения движущейся точки. Из курса математического анализа известно, что в пределе, при Dt®0, когда D r ®0, секущая некоторой кривой совпадает с касательной к ней, поэтому мгновенная скорость V направлена по касательной к траектории.
Мгновенная скорость V, как и средняя, показывает, какое перемещение совершила бы движущаяся материальная точка за единицу времени, обладая постоянной скоростью V.
· Средняяпутеваяскорость – скалярная величина, равная отношению всего пути, пройденного материальной точкой, ко всему времени движения, т. е. к промежутку времени, за который этот путь был пройден:
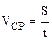 .
.
Очевидно, мгновенная скорость движения материальной точки может меняться во времени. Характеристикой такого изменения служит ускорение.
· Среднееускорение равно отношению изменения скорости D V к промежутку времени Dt, за которое это изменение произошло:
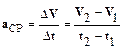 .
.
Положив в этом определении Dt=1с, легко понять, что среднее ускорение показывает, на сколько изменилась скорость за единицу времени. Измеряется ускорение в следующих единицах:
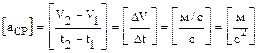 .
.
Ускорение, подобно скорости, может изменяться с течением времени.
· Мгновенноеускорение – это ускорение материальной точки в данный момент времени, в данной точке траектории.
Проводя рассуждения, как при определении мгновенной скорости, можно сделать вывод, что:
· Ускорение – векторная физическая величина равная первой производной скорости материальной точки по времени или, соответственно, второй производной ее радиус-вектора по времени:
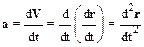 .
.
Положив в соотношении (1.7) промежуток времени dt=1c, получим 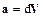 , что позволяет понять физический смысл ускорения. Ускорение показывает, на сколько изменяется скорость за единицу времени.
, что позволяет понять физический смысл ускорения. Ускорение показывает, на сколько изменяется скорость за единицу времени.
1.3. Равномерное и равнопеременное движение
Существует несколько классификаций движения по тому или иному признаку. Так, механическое движение подразделяют на равномерное и неравномерное.
· Равномерное движение – можно определить несколькими способами:
1. равномерное движение – это движение, при котором за любые равные промежутки времени материальная точка (тело) совершает одинаковые перемещения,
2. равномерное движение – это движение с постоянной скоростью,
3. равномерное движение – это движение, при котором ускорение равно нулю.
· Неравномернымдвижением материальной точки называют движение, при котором скорость меняется с течением времени.
Одной из характеристик неравномерного движения является ускорение. Простейший вид неравномерного движения – равнопеременное движение.
· Равнопеременное движение – это:
1. движение, при котором за любые равные промежутки времени скорость точки (тела) изменяется на одну и ту же величину,
2. движение, при котором ускорение а материальной точки остается постоянным.
Интегрируя соотношения, определяющие мгновенную скорость (1.4) и мгновенное ускорение (1.7), можно получить основные законы кинематики материальной точки.
· Законыкинематики:
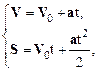
первое из уравнений системы называется законом изменения скорости – V = V (t), второе – законом движения – S = S (t); V 0 – начальная скорость, т. е. скорость материальной точки в момент времени t=0, a – ее ускорение.
Законы (1.8) включают в себя два частных случая:
1. Равнопеременное движение без начальной скорости: начальная скорость V 0 равна нулю, ускорение а не равно нулю и
2. Равномерное движение со скоростью V 0 и ускорением а равным нулю. Законы кинематики в этих случаях принимают следующий вид:
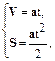
| и | 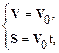
|
В координатной записи уравнения (1.8) имеют следующий вид:
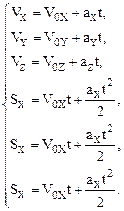 (1.8а)
(1.8а)
Закон движения – S = S (t) позволяет определить координаты движущейся материальной точки в произвольный момент времени. Учитывая, что S = r 1 – r 0 запишем:
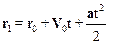 .
.
Из последнего соотношения следует, что координата Х в момент t равна
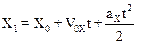 .
.
Механические движенияразличаются также по виду траекторий: прямолинейное, вращательное и криволинейное. Если модуль перемещения ½dr½=dr по величине равен пройденному пути ds, то материальная точка движется по прямой линии. В этом случае модуль мгновенной скорости равен первой производной пути по времени:
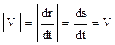 .
.
Соотношение (1.9) – основное при решении задач по кинематике. Интегрируя его, можно найти длину пути, пройденного телом за время от t1 до t2:
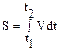 .
.
Для равномерного движения со скоростью V=const из (1.10) следует:
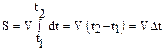 ,
,
здесь Dt=(t2-t1) – время движения.
1.4. Кинематика движения по окружности
Если материальная точка М движется по окружности (см. рис. 1.3), то ее положение определяют вектором угла d j [1], который образован ее радиус-вектором R с некоторой, произвольно выбранной осью Х.
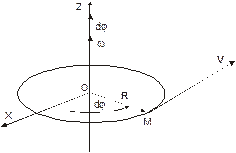
| Рис.1. 3. На рисунке обозначены: V – линейная скорость, dj – угол поворота радиус-вектора точки за время dt, dj – вектор угла поворота, w– угловая скорость |
Вектор угла d j можно определить следующим образом:
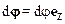 ,
,
здесь e Z – единичный вектор оси вращения Z. Заметим, что модуль радиус-вектора материальной точки равен радиусу окружности, по которой она движется: ½ R ½=R.
При решении задач удобно выбрать направление оси Х так, чтобы она проходила через начальное положение движущейся точки. Модуль вектора угла dj численно равен углу поворота радиус-вектора, измеренному в радианах; направление d j определяется по одной из альтернативных (Б.I) формулировок правила буравчика (правого винта).
· Правилобуравчика (Б.I): если расположить ось буравчика вдоль оси вращения и вращать его рукоятки в направлении движения материальной точки (в направлении ее линейной скорости), то направление поступательного движения конца буравчика укажет направление вектора угла d j.
Движениематериальной точки (а также центра масс материального тела) по окружности характеризуется угловой скоростью ω и угловым ускорением e. Как в кинематике поступательного движения, можно ввести понятие средней и мгновенной угловой скорости, углового ускорения.
· Средняяугловаяскорость w CP равна отношению угла поворота D j радиус-вектора материальной точки ко времени Dt, за которое этот поворот произошел:
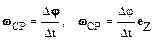 ,
,
где e Z – единичный вектор оси вращения Z.
Средняя угловая скорость w CP показывает, на какой угол повернулся радиус-вектор материальной точки за единицу времени. Измеряется она в единицах рад/c, чаще, опуская наименование "радиан" используют секунду в минус первой степени (с –1).
· Мгновенная у гловаяскорость – это угловая скорость движения материальной точки в данный момент времени, в данной точке траектории.
· Мгновенная у гловаяскорость ω – векторная физическая величина, равная первой производной угла поворота радиус-вектора материальной точки по времени:
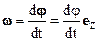
Физический смысл мгновенной и средней угловой скорости одинаков – они характеризуют угол, на который повернулся радиус-вектор за единицу времени. Соотношения (1.12) и (1.13) указывают, что векторы угловой скорости параллельны вектору угла поворота d j.
· Векторы средней и мгновенной угловой скорости откладывают на оси вращения, их направление определяется по правилу (Б.I) буравчика (правого винта):
если расположить буравчик вдоль оси вращения и вращать рукоятки в направлении движения материальной точки (в направлении ее линейной скорости), то направление поступательного движения конца буравчика укажет направление вектора угловой скорости.
· Среднееугловоеускорение e (или b)– векторная величина, равная отношению приращения угловой скорости D w к промежутку времени, за который это изменение произошло:
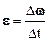 .
.
Угловое ускорение показывает, на сколько изменилась угловая скорость за единицу времени.
· Мгновенноеугловоеускорение e (или b) – векторная величина, равная первой производной угловой скорости w или второй производной угла j поворота по времени:
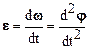
Угловое ускорение измеряется в рад/с2, или с –2. Как следует из (1.12) и (1.13), угловое ускорение откладывают на оси вращения. При условии, что вектор e совпадает по направлению с вектором угловой скорости ω, имеет место ускоренное вращение, если вектор e направлен противоположно вектору ω, то характер вращения – замедленный.
Основными характеристиками вращательного движения являются:
· периодвращения (обращения) Т – время одного полного оборота.
· частота вращенияn (используют также обозначения f, или n) – число полных оборотов в единицу времени.
Период вращения Т измеряется в секундах ([T]=c), частота вращения в с–1 ([n]=c-1).
Очевидна связь частоты и периода вращения:
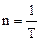 .
.
Положив в соотношении (1.12) Dj=2p и Dt=T, получим для средней угловой скорости:
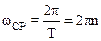 ..
..
При равнопеременном вращательном движении угол поворота j, угловая скорость w и угловое ускорение e связаны соотношениями, аналогичными соотношениям, полученным для поступательного движения. Интегрируя соотношения (1.13) и (1.15), приходим к основным уравнениям кинематикивращательного движения:
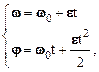
здесь w 0 – начальная угловая скорость.
Эти уравнения решают основную задачу кинематики для вращательного движения, если известны начальная угловая скорость w 0 и угловое ускорение e.
Приведем важное соотношение, определяющее число N оборотов, совершенных телом:
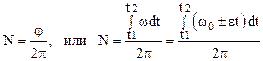 ,
,
где положительный знак пишется при ускоренном вращении, знак минус – при замедленном.
1.5. Взаимосвязь угловых и линейных
характеристик при движении по окружности
Обратимся вновь к рисунку 1.3, чтобы установить связь линейной и угловой скоростейпри движении по окружности. Для бесконечно малого угла поворота dφ путь dS, пройденный частицей равен длине дуги окружности, т. е.:
dS=Rdj.
На основании соотношения (1.9) модуль V линейной скорости найдем дифференцированием:
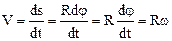
· Векторноепроизведениевекторов a и b есть вектор с (обозначается c =[ a, b ]), модуль которого равен произведению модулей векторов-сомножителей на синус угла между этими векторами. Направление вектора векторного произведения определяется по правилу буравчика (Б.II).
· Правилобуравчика (Б.II) для нахождения направления вектора векторного произведения c =[ a, b ]:
1. отложить векторы a и b от одной точки,
2. провести через них плоскость,
3. расположить буравчик перпендикулярно полученной плоскости,
4. вращать рукоятки буравчика от первого вектора-сомножителя a ко второму b в направлении меньшего угла,
5. направление поступательного движения конца буравчика укажет направление вектора с векторного произведения.

|
Рис. 1.4.
К определению векторного произведения векторов.
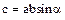 , или , или 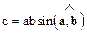 , где , где 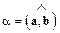 .
Модуль векторного произведения векторов равен площади параллелограмма, построенного на векторах сомножителях a и b, как на сторонах .
Модуль векторного произведения векторов равен площади параллелограмма, построенного на векторах сомножителях a и b, как на сторонах
|
Анализируя направления векторов V, R и w (см. рис. 1.3) приходим к выводу, что они связаны посредством следующего векторного произведения:
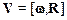 .
.
Формулу (1.21) называют формулойЭйлера.
Покажем, что движение материальной точки по окружности с постоянной по модулю линейной скоростью представляет собой равнопеременное движение. Поскольку мгновенная линейная скорость V всегда направлена по касательной к траектории в данной ее точке, то (см. рис. 1.5), оставаясь постоянной по модулю, она непрерывно изменяется по направлению, поэтому скорости движущейся точки в положениях А и В не равны: V A ¹ V B. Изменение вектора скорости свидетельствует о том, что материальная точка на окружности испытывает ускорение.
|
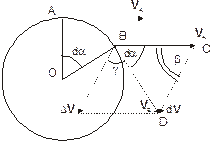
| Рис. 1.5. К анализу равномерного вращательного движения точки. AB=ОА=R, R – радиус окружности |
Пусть в момент времени t материальная точка находилась в точке А траектории, а через малый промежуток времени dt переместилась в близко расположенную точку В (на рисунке 1.5 дуга АВ для наглядности показана увеличенной). Изменение скорости за время dt равно разности d V=V B – V A, показанной на рисунке.
Рассмотрим треугольники АОВ и CВD. Эти треугольники подобны: они равнобедренные (OA=OB=R и ВС=BD=V) и имеют равные углы ÐAOB=ÐDBC=da (это углы со взаимно перпендикулярными сторонами). Из подобия треугольников АОВ и CВD следует, что
AB:AO=DC:BD. (*)
Длина дуги AB=Rda (da – центральный угол, опирающийся на дугу АВ), из треугольника ОАВ выразим хорду АВ: AB=2Rsin(da/2)»Rda. Для бесконечно малого промежутка времени dt угол da мал, поэтому длина дуги приблизительно равна хорде:
CD=dV=2Vsin(da/2)»Vda=adt.
Подставляя полученные величины отрезков в пропорцию (*), имеем
Rda:R=adt:V.
Откуда следует: что величина ускорения численно равна:
a=dV/dt=Vda/dt=Vw. (**)
Используя соотношение (1.20) получим, что
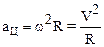 .
.
Для определения направления вектора ускорения рассмотрим треугольник ВСD. Направление вектора а, как уже отмечено, совпадает с направлением вектора d V, в нашем случае – с направлением отрезка CD. Из треугольника ВCD следует, что угол b – угол между векторами V А и d V равен (p-da)/2. Очевидно, что при da®0 угол b®p/2. Таким образом, вектор d V, а значит и вектор ускорения а, при dt®0 стремятся к положению нормали к вектору скорости V.
Таким образом, при движении по окружности с постоянной по величине линейной (или угловой) скоростью, материальная точка испытывает постоянное ускорение, направленное по радиусу к ее центру. Такое ускорениеназывают центростремительным. Формулу для центростремительного ускорения в векторном виде записывают, используя векторное произведение векторов линейной V и угловой w скорости:
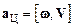 .
.
Используя соотношение (1.21) и векторное тождество
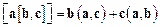
последнюю формулу можно записать так:
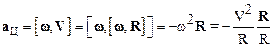 .
.
Вектор R /R= n – есть вектор внешней нормали к траектории.
1.6. Нормальное, тангенциальное и полное ускорения
Взаимосвязь угловых и линейных характеристик можно рассмотреть на основе общих соображений. Пусть V мгновенная линейная скорость материальной точки, движущейся по окружности, w – ее угловая скорость. Введем единичный вектор касательной t, связанный с движущейся материальной точкой. Тогда скорость V можно записать так:
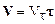 ,
,
здесь Vt=V – проекция вектора скорости на направление вектора касательной. Дифференцируя (1.25) по времени, получим:
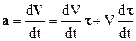 .
.
Преобразуем второй член последнего соотношения:
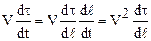 .
.
Как видно из рисунка (1.5)
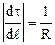 .
.
Направление d t /dℓ совпадает с направлением вектора внутренней нормали n. Окончательно (1.26) запишем следующим образом:
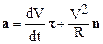 .
.
В соотношении (1.29) первое слагаемое представляет собой тангенциальной ускорение а t, второе – нормальное а Н или центростремительное ускорение. Таким образом,
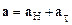 :
:
полное ускорениедвижущейся точки равно векторной сумме нормального и тангенциального ускорений. Модуль полного ускорения определяется соотношением:
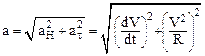
Воспользуемся формулой Эйлера (1.21): 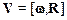 . Дифференцируя по времени (1.31), имеем:
. Дифференцируя по времени (1.31), имеем:
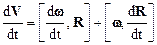 ,
,
где d w /dt= e угловое ускорение, d R /dt= V – мгновенная линейная скорость материальной точки.
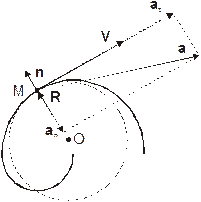
| Рис. 1.6. V – мгновенная линейная скорость, at – тангенциальное, an – нормальное и a – полное ускорение частицы. О – центр касательной окружности радиусом R, n – внешняя нормаль к траектории движения |
Из рисунка 1.6 видно, что множитель 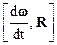 представляет собой тангенциальное ускорение, а
представляет собой тангенциальное ускорение, а 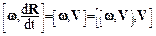 – нормальное или центростремительное ускорение.
– нормальное или центростремительное ускорение.
Таким образом (1.32) можно привести к виду: 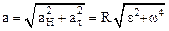 . (1.32а)
. (1.32а)
1.7. Кинематика произвольного криволинейного движения
В общем случае неравномерного движения материальной точки по криволинейной траектории, ускорение а равно сумме нормального а Н (центростремительного) и тангенциального аt ускорений:
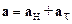 .
.
Вектор тангенциального ускорения ατ направленпо касательной к траектории, вектор α Н– по нормали к траектории (центростремительное ускорение); αn характеризует изменение направления скорости со временем, а t – характеризует изменение модуля скорости.
Величины α n и α τ определяют характер движения материальной точки.
1. α Н=0, α τ=0 – прямолинейное равномерное движение,
2. α Н=0, α τ=const – прямолинейное равнопеременное движение,
3. α Н=const¹0, α τ=0 – движение по окружности с постоянной по величине скоростью,
4. α Н¹0, α τ=const, при R=const равнопеременное движение по окружности,
5. α Н¹0, α τ¹0 – криволинейное неравномерное движение.
1.8. Кинематика колебательного движения
· Колебания – это движения или процессы, обладающие той или иной степенью повторяемости во времени.
Колебания широко распространены в природе и имеют место в самых разнообразных явлениях, например, качание маятника пружинных часов, мигание индикатора таймера, изменение значения переменного тока, величины напряжения на обкладках конденсатора, включенного в колебательный контур и т. п. Повторяющиеся процессы протекают внутри живых организмов, например, биение сердца, чередование промежутков сна и бодрствования, ритмы, сопровождающие работу человеческого мозга. Таким образом, колебания присутствуют как в живой, так и в неживой природе; в микроскопических и макроскопических процессах.
Важнейшая особенность колебательного движения состоит в том, что оно происходит в системах, занимающих ограниченную часть пространства. Так, совершая колебательное механическое движение, система движется около некоторого положения равновесия, но энергия системы не выходит за пределы границ системы. Колеблющаяся величина, заключена в некоторый интервал, содержащий ее среднее значение. Несмотря на качественное различие тех или иных колебательных процессов, все они могут быть описаны одними и теми же количественными законами.
· Свободные, или собственные колебания– это колебания, которые происходят в системе, выведенной из состояния равновесия и предоставленной самой себе.
· Гармоническимиколебаниями называют колебания, при которых колеблющаяся величина изменяется во времени по закону синуса или косинуса. Гармонические колебания представляют собой простейшие колебания.
Уравнение гармоническименяющейся величины x может быть как с помощью функции синуса, так и с помощью функции косинуса следующим образом:
 .
.
В формулу (1.33) входят следующие величины:
· Амплитуда колебаний А – наибольшее значение колеблющейся величины x. Из (1.33) следует, что А>0.
· Фазаколебаний – 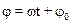 – аргумент функции синуса или косинуса в уравнении гармонического колебания.
– аргумент функции синуса или косинуса в уравнении гармонического колебания.
· Начальнаяфаза колебаний– 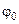 значение фазы j в момент времени t=0.
значение фазы j в момент времени t=0.
При необходимости, переход от функции синуса к функции косинуса осуществляется по формулам приведения, при этом изменяется начальная фаза колебаний. Например, в формулах (1.33) 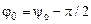 .
.
· Периодколебаний Т – это время, за которое совершается одно полное колебание.
· Можно говорить, что период – это наименьший промежуток времени, по истечении которого колеблющаяся величина x имеет то же самое значение и ту же скорость изменения.
· Частота колебанийn (n, или f) – величина обратная периоду колебаний
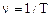 .
.
· Круговая, илициклическая, частота w связана с частотой n соотношением
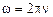 .
.
Измеряется циклическая частота в с –1. Она показывает, какое число колебаний происходит за 2p секунд.
Используя определение периодичной функции – F(х)=F(х+Т), запишем:
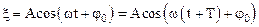 .
.
Поскольку функция 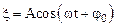 имеет период 2p, то сравнение фаз колебаний позволяет установить связь периода колебаний с циклической частотой:
имеет период 2p, то сравнение фаз колебаний позволяет установить связь периода колебаний с циклической частотой:
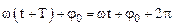 ,
,
отсюда следует, что
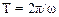 .
.
Частота показывает, какое число колебаний совершается за единицу времени (секунду). Измеряется частота в герцах: 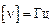 . 1 Гц – это такая частота, при которой в единицу времени совершается одно колебание.
. 1 Гц – это такая частота, при которой в единицу времени совершается одно колебание.
Скоростьизменения V и ускорение – a колеблющейся величины x определяется обычным образом (по формулам (1.4) и (1.7)):
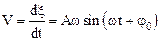
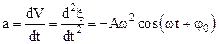
Начальную фазу колебаний, можно определить с помощью первого из уравнений (1.33) по известным начальным условиям x0, V0:
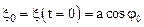 и
и 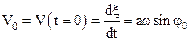 .
.
Откуда следует:
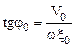 .
.
Амплитуду гармонически колеблющейся величины можно вычислить по формуле:
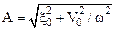
Пусть материальная точка одновременно участвует в двух колебаниях x1 и x2 одного направления и одной частоты w:
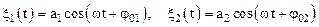
По принципу суперпозиции результирующее смещение равно алгебраической сумме смещений, полученных в каждом из колебаний, т. е.:
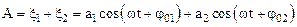 .
.
Предположим, что амплитуды обоих колебаний равны, т. е. а1=а2=а. Используем тригонометрическую формулу для суммы двух косинусов и преобразуем формулу (1.39):
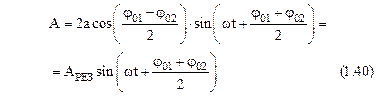
Таким образом, при суперпозиции колебаний одной частоты, одного направления и одинаковой амплитуды возникает гармоническое колебание с той же самой частотой w, и амплитудой, зависящей от разности начальных фаз колебаний и равной
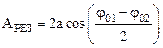 .
.
В частности: при j10=j20 имеем АРЕЗ=2а, при j10=j20±p амплитуда результирующего колебания равна нулю.
1.8.2. Биения
Рассмотрим суперпозицию двух гармонических колебаний одинаковой амплитуды и одного направления, частоты которых w1 и w2 отличаются незначительно (w1»w2=w)
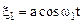 ,
, 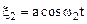 .
.
Результирующее колебание равно:
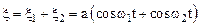 .
.
Используя известные тригонометрические формулы, приведем (1.41) к следующему виду
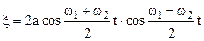 .
.
Очевидно, что первый сомножитель гармонически изменяется с частотой w=(w1+w2)/2»w1»w2. Второй множитель осциллирует с малой частотой (w1-w2)/2, а значит, имеет большой период. Таким образом, колебание (1.43) можно рассматривать как гармоническое колебание с частотой w:
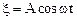 ,
,
амплитуда которого А равна:
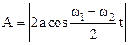 .
.
Амплитуда медленно изменяется во времени – пульсирует.
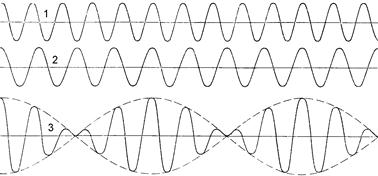
Характер изменения во времени величины x, порожденной наложением колебаний с отношением частот 8:10 показан на рисунке 1.7.
Изображенное на рисунке постепенное нарастание и уменьшение амплитуды результирующих колебаний и носит название “биения”.
Используя условие периодичности функции x(t)=x(t+T) можно показать, что при рациональном отношении частот колебаний w1:w2=n1:n2, (n1:n2 – целые числа) функция x является периодической с периодом Т равным
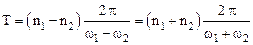 .
.
|
| Рис. 1.7. |
| (1) - колебания x1 = а cos 10wt, (2) колебание x2 = а cos 8wt, (3) результирующее колебание |
Если частоты исходных колебаний не соизмеримы, т. е. их отношение w1:w2 не равно отношению некоторых целых чисел n1 и n2, то результирующее колебание не является периодическим.
1.8.3. Сложение взаимно перпендикулярных колебаний
Сложение колебаний c рациональным отношением частот, но направленных вдоль взаимно перпендикулярных осей X и Y
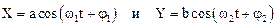
экспериментально исследовал А. Лиссажу. Он показал, что точка, участвующая в таких колебаниях, движется по плоским замкнутым траекториям, которые получили, в последствии, название фигурЛиссажу.
Пусть материальная точка участвует в двух колебаниях, определяемых уравнениями (1.46). Найдем уравнение траектории Ф(X,Y)=0 материальной точки на координатной плоскости X,Y. Для упрощения предположим, что частоты колебаний равны, а начальная фаза первого колебания равна нулю (этого можно добиться соответствующим выбором начального момента времени), начальную фазу второго колебания обозначим через j. Уравнения колебаний примут вид:
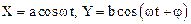 .
.
Для нахождения траектории (исключения параметра t) поступим следующим образом: из первого уравнения системы (1.47) выразим coswt,
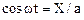 ,
,
тогда:
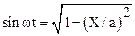 .
.
Представляя cos(wt+j) как косинус суммы двух углов из второго уравнения (1.47) имеем
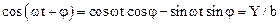 .
.
Используя выражения для тригонометрических функций аргумента wt, соотношение (1.48) можно записать следующим образом:
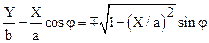 .
.
Возводя в квадрат и произведя перегруппировку, получим:
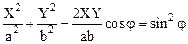 .
.
Из аналитической геометрии известно, что уравнение (1.49) является уравнением эллипса, оси которого повернуты относительно осей координат X и Y. Ориентация осей эллипса и размеры его полуосей достаточно сложно зависят от разности фаз колебаний j=j2-j1=j2.
Частные случаи.
1. Разность фаз исходных колебаний равна нулю (j=0). Уравнение (1.49) принимает вид:
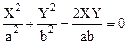 ,
,
т. е. представляет собой полный квадрат, поэтому:
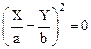 .
.
Решением полученного уравнения является функция
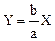 .
.
2. Разность фаз колебаний равна ±p. Уравнение (1.49) приводится к виду
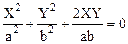 .
.
Аналогично предыдущему случаю получаем:
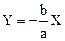 .
.
Уравнения (1.50) и (1.51) являются уравнениями прямых, тангенсы наклона которых равны b/a и -b/a, соответственно. Частица движется по соответствующей диагонали прямоугольника ABCD со сторонами a и b (см. рис. 1.8).
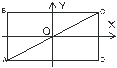 а
а
| 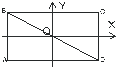 b
b
| Рис. 1.8. a - движение описывается уравнением (1.50), и b - уравнением (1.51) |
3. Разность фаз колебаний равна p/2. Уравнение результирующего движения (1.49) принимает вид
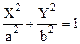 ,
,
т. е. представляет собой эллипс, приведенный к координатным осям X и Y, полуоси эллипса равны амплитудам a и b складывающихся колебаний.
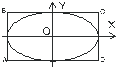
| Рис. 1.9. Результат наложения взаимноперпендикулярных колебаний с разностью фаз равной p/2 |
4. При произвольной разности фаз j колебаний траектория представляет собой эллипс, вписанный в прямоугольник со сторонами 2a и 2b. Траектории, рассмотренные в пунктах 1 и 2 можно рассматривать как эллипсы, вырожденные в отрезок. Если полуоси эллипса (амплитуды складываемых колебаний) равны между собой, то эллипс вырождается в окружность (a=b).
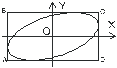
| Рис. 1.10. Результат наложения взаимно перпендикулярных колебаний с произвольной разностью фаз |
5. Разность фаз j определяет также направление движения материальной точки по траектории. Уравнения (1.47) в параметрической форме при величине j равной -p/2 могут быть записаны так:
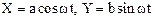 .
.
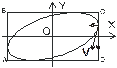
После начала движения, т. е. при t>0 величина Х начнет уменьшаться, Y – будучи величиной положительной, будет возрастать. Этим изменениям, как видно из рисунка 1.11а, соответствует движение материальной точки со скоростью V против направления движения часовой стрелки. Если разность фаз j равна p/2, то уравнения (1.47) имеют вид
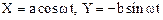
с началом движения координаты X и Y будут уменьшаться, что указывает на то, что точка движется по эллипсу в направлении движения часовой стрелки (см. рис. 1.11b).
6. Если частоты взаимно перпендикулярных колебаний не равны друг другу (wX¹wY), то траектории движущихся точек представляются сложными кривыми. Во всех случаях, когда отношение wX/wY является рациональным числом, траектория точки является замкнутой линией. Вид траектории зависит также от разности фаз исходных колебаний.
 a
a
|
 b
b
| Рис 1.11. К вопросу о направлении движения частицы. Vуказывает направление скоростей частиц, стрелки – составляющие скоростей вдоль осей координат |
Если отношение частот колебаний вдоль осей Х и Y (wX:wY) не является рациональным числом, то траектория точки, участвующей в этих колебаниях – незамкнутая линия. С течением времени линия заполняет равномерно всю прямоугольную часть координатной плоскости размером 2a ´ 2b.
1.9. Кинематикаволнового движения
· Волной, или волновым движением, называют процесс распространения колебаний.
Волны, в отличие от колебаний, локализованных в некоторой конечной области пространства, могут распространяться не только в закрытых системах, но и в открытых. Открытыми системами называют системы, не имеющие пространственных границ, или, наоборот, системы, ограниченные какими-либо стенками с поглощающими покрытиями. Благодаря этим условиям в открытых системах отсутствует отражение и возвратное движение волн, а значит, отсутствуют такие явления, как эхо и резонанс.
Волны, как и колебания, необыкновенно широко распространены в окружающем мире; они очень разнообразны по физической природе. Выделяют упругие механические волны, звуковые волны, называемые просто звуком, световые волны и радиоволны, плазменные, волны вероятности и др. С формальной точки зрения все волны описываются одним и тем же уравнением.
Волны, образованные за счет внешнего периодического воздействия, называются бегущими волнами. Если внешняя сила, вызывающая колебания источника, является гармонической, то вызванная ею волна будет также гармонической.
|
|
Дата добавления: 2013-12-12; Просмотров: 579; Нарушение авторских прав?; Мы поможем в написании вашей работы!