
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение задач по динамике движения материальной точки по окружности
|
|
|
|
Пример 2.4.
Определить угол между вертикальной осью конического маятника и нитью, если тело движется с постоянной угловой скоростью w. Длина невесомой нити подвеса L.
Решение
a=?
w, L, g=9,8 м/с2
|
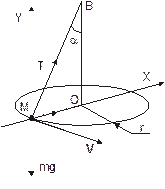
Пусть масса конического маятника равна m. Движение материальной точки происходит в горизонтальной плоскости под действием силы натяжения нити Т и силы тяжести m g (см. рисунок).
Основной закон динамики для данной задачи имеет вид:
m a = Т + m g. (1)
Выберем начало системы координат в центре движущегося по окружности тела так, чтобы ось Х проходила через центр окружности, а ось Y направим вверх. Проецируя уравнение (1) на оси, имеем:
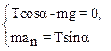 (2)
(2)
Нормальное ускорение материальной точки аn = w2r. Из чертежа следует, что радиус траектории маятника r=ОМ равен r=Lsina, где L=МВ – длина подвеса. Используя дополнительные соотношения, преобразуем уравнения системы (2):
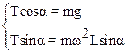 (3)
(3)
Из уравнений (3) следует:
cosa = g/w2L,
или
a = arccos(g/w2L).
Пример 2.5.
На веревке длиной R = 1м висит груз массой m = 5 кг. Максимальное натяжение, которое может выдержать веревка, TMAX = 60 Н. Оборвется ли веревка, если ее отклонить на угол a = 30°? На какой максимальный угол можно отклонить веревку, чтобы она не разорвалась?
| aMAX=? ОА=R=1м, m=5 кг, TMAX=60 H, a=30° | 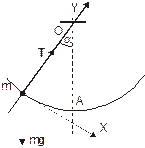
|
Решение.
На груз m действуют две силы: сила тяжести m g и сила натяжения Т. Основной закон динамики принимает вид:
m a = m g + Т. (1)
Выберем начало системы координат в центре движущегося по окружности тела так, чтобы ось Y проходила через центр окружности, а ось Х направим по касательной.
Проецируя уравнение (1) на оси Y и X имеем:
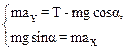 (2)
(2)
Ускорение ах, входящее во второе уравнение системы (2) представляет собой тангенциальное ускорение и указывает, что модуль скорости движущегося тела меняется с течением времени. Сила натяжения Т в точке А определяется первым из уравнений (2):
|
|
|
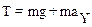 (3)
(3)
Ускорение aY, есть нормальное или центростремительное, ускорение аn. Очевидно, что максимальное натяжение веревка испытывает в точке А, так как в этой точке тело имеет максимальную скорость, а значит – максимальное нормальное ускорение. Используя выражение aY=аn=V2/R для нормального ускорения, преобразуем уравнение (3):
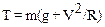 (4)
(4)
Скорость тела в точке А можно определить с помощью закона сохранения механической энергии. В точке наибольшего отклонения полная механическая энергия – это потенциальная энергия еП = mgh, где h = R(1- соsa). В точке А механическая энергия равна кинетической (за нулевой уровень потенциальной энергии удобно принять уровень соответствующий нижней точке А). Уравнение закона сохранения энергии запишем так:
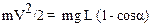 .
.
Откуда получим, что квадрат скорости с точке А равен
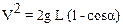 . (5)
. (5)
Подставляя в (4) выражение (5) получим окончательно для силы натяжения:
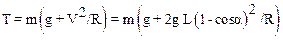 . (6)
. (6)
Подставляя в (6) максимальное значение силы Т=Тmax можно определить угол при котором веревка оборвется, т. к. достигается предельное усилие. Расчеты дают что amax=45°.
Итак, если веревку отклонить на 30°, то она не оборвется.
Пример 2.6.
Тело скатывается с вершины гладкой сферической поверхности радиуса R. Найти, при какой скорости тело оторвется от поверхности. Считать, что трение отсутствует.
Решение.
| H=? R m=0 | 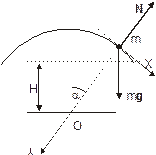
|
На скользящее тело действуют сила тяжести m g и сила N нормальной реакции полусферы. Уравнение движения имеет вид
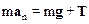 . (1)
. (1)
Направим ось Х по касательной поверхности полусферы, ось Y – радиально в направлении ее центра. Проецируя уравнение (1) на оси получим:
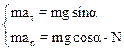
Преобразуем полученные уравнения.
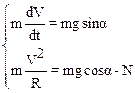 (3)
(3)
Если учесть, что время движения dt может быть вычислено по формуле dt=dℓ/V, где dℓ=Rda, то первое уравнение приводится к следующему виду
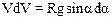 .
.
Интегрируя последнее по V и a, получим соотношение
|
|
|
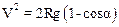 . (4)
. (4)
В момент отрыва тела от полусферы реакция опоры обращается в ноль, и второе из уравнений (3) принимает вид
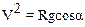 (5)
(5)
исключив a из соотношений (4) и (5) найдем
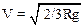 .
.
Пример 2.7.
Найти максимальную разность между силами натяжения нити при вращении в вертикальной плоскости шарика массой m на невесомой нити.
Решение
| (Т1-Т2)МАХ=? m | 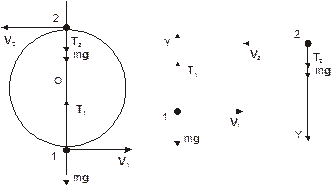
|
На шарик действуют две силы: сила натяжения Т и сила тяжести m g. Уравнение движения (второй закон Ньютона) запишется так:
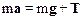 . (1)
. (1)
Для нахождения максимальной разности между силами натяжения, возникающими при вращении шарика, вычислим силы натяжение нити в точках 1 и 2.
Для положения 1 уравнение движения в проекции на оси координат "1" запишется в виде:
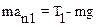 , (2)
, (2)
где 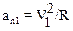 .
.
Аналогично, в положении 2 для проекций в системе координат "2" имеем:
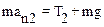 . (3)
. (3)
так как 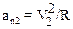 , то из (2) и (3) имеем
, то из (2) и (3) имеем
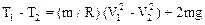 (4)
(4)
Разность 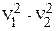 определим из закона сохранения энергии. Если выбрать за нулевой уровень отсчета потенциальной энергии уровень точки 1, то можно записать, что
определим из закона сохранения энергии. Если выбрать за нулевой уровень отсчета потенциальной энергии уровень точки 1, то можно записать, что
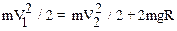 .
.
Следовательно,
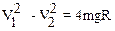 . (5)
. (5)
Подставляя (5) в соотношение (4) имеем окончательно
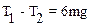 .
.
Пример 2.8.
Вал в виде сплошного цилиндра массой m=10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m1=2 кг. С каким ускорением a будет опускаться гиря, если её предоставить самой себе.
a=?
m=10 кг, m1=2 кг
Решение
В задаче участвуют два тела, совершающие различные движения: тело m1 движется прямолинейно, вал – вращается. Уравнения движения имеют следующий вид:
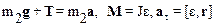 , (1)
, (1)
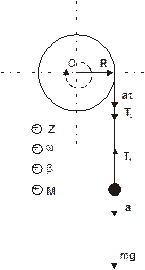
в системе уравнений (1) введены обозначения: а t – тангенциальное ускорение точек на периферии вала, Т – сила натяжения шнура, r – радиус вала, М – момент, вращающий вал, а – ускорение тела m1.
|
Момент, вращающий вал равен 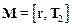 , J – момент инерции вала относительно геометрической оси. Рассматривая вал как однородный цилиндр, считаем, что его момент инерции равен J = 1/2m1r2.
, J – момент инерции вала относительно геометрической оси. Рассматривая вал как однородный цилиндр, считаем, что его момент инерции равен J = 1/2m1r2.
Определим направление векторных величин (по правилу буравчика) и выбрав направление осей координат как показано на рисунке запишем систему (1) в проекциях.
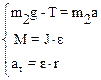 (2)
(2)
При условии, что шнур нерастяжим и отсутствует его скольжение по поверхности вала тангенциальное ускорение а t по модулю равно поступательному ускорению а груза m1: аt=а. С учетом дополнительных соотношений уравнения системы (1) примут вид:
|
|
|
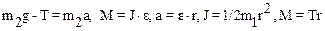 (3) Решая систему относительно ускорения a получим:
(3) Решая систему относительно ускорения a получим:
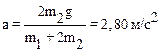 .
.
Пример 11.
Через блок в виде диска, имеющий массу m=80г, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m1=100г и m2=200г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.
Решение.
| а1, а2=? m=80 г=8×10–2 кг m1=100 г =10–1 кг m2=200 г=2×10–1 кг | 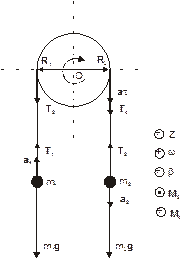
|
Рассматриваемая в задаче система состоит из двух движущихся поступательно грузов и одного вращающегося диска. На каждый из грузов действует две силы: сила тяжести m g, направленная вниз, и сила Т натяжения нити, направленная вверх. Запишем законы поступательного и вращательного движения этих тел.
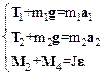 (1)
(1)
Результирующий вращающий момент, приложенный к диску, равен
М = М 2+ М 4=[ R 1, T 2]+[ R 2, T 4],
R 1 и R 2 – радиус-векторы точек приложения сил натяжения нити T 2 и T 4. Предположим, что m2 > m1, поэтому ускорения грузов будет направлено, как показано на рисунке. Выберем произвольное направление осей координат (например, как на рисунке) и запишем систему уравнений в проекциях.
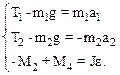 (2)
(2)
При условии, что нить нерастяжима, отсутствует ее скольжение по поверхности диска, тангенциальное ускорение точек на поверхности диска а t по модулю равно поступательному ускорению а грузов: аt=а. Угловое ускорение диска связано с линейным ускорением грузов соотношением 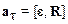 ; в скалярной форме
; в скалярной форме 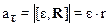 . Пренебрегая массой нити приходим к выводу, что силы натяжения Т1 и Т2 равны по величине. Учтем также, что момент инерции диска J = mr2/2. С учетом приведенных дополнительных соотношений система (2) принимает вид:
. Пренебрегая массой нити приходим к выводу, что силы натяжения Т1 и Т2 равны по величине. Учтем также, что момент инерции диска J = mr2/2. С учетом приведенных дополнительных соотношений система (2) принимает вид:
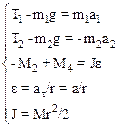
Решая полученную систему, получим
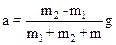 .
.
После подстановки числовых значений имеем
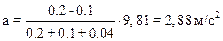
Задачи к главе 2 для самостоятельного решения
2.1. Определить, на каком расстоянии от поверхности Земли должен находиться спутник, если он вращается в плоскости экватора с периодом, равным периоду вращения Земли вокруг оси.
35870 км.
2.2. Какова должна быть продолжительность суток на Земле, чтобы тела, находящиеся на экваторе, были невесомы.
|
|
|
1,41 часа.
2.3. Тело массой 1 кг, закрепленное на конце невесомого стержня длиной 0,5 м, вращается в вертикальной плоскости в поле силы тяжести с постоянной частотой 0,2Гц. Вычислить разность сил, действующих на стержень в нижнем и верхнем положении.
1,6 Н.
2.4. Камень массой 0,5 кг, привязанный к веревке длиной 50 см, вращается в вертикальной плоскости. Сила натяжения веревки в нижней точке окружности равна 44 Н. На какую высоту поднимется камень, если веревка отрывается в тот момент, когда его скорость направлена вертикально вверх?
2 м.
2.5. Определить плотность планеты, если тела на ее экваторе невесомы. Период обращения планеты вокруг оси – Т = 20 ч.
r = 27, 25кг/м3.
2.6. Определить максимальную силу натяжения, которую выдерживает нить, к концу которой привязан шарик массой m = 500 г, если она разрывается, когда ее отклоняют на угол, больший 60°.
Т = 9,8Н.
2.7. На горизонтально вращающемся диске на расстоянии 1 м от вертикальной оси вращения лежит груз. При каком числе n оборотов в секунду груз начнет скользить, если коэффициент трения между грузом и диском 0,01?
n = 0,05 об/с.
2.8. Маленький шарик массы m, подвешенный на невесомой нити, отклоняют от положения равновесия на угол a = 60° и отпускают. Определить натяжение нити в начальный момент движения.
Т = mg/2.
2.9. В конусе лежит шарик. Конус начинают вращать с угловой скоростью w. На каком расстоянии от вершины конуса шарик будет находиться в состоянии равновесия? Угол раствора конуса равен 2a.
L=g/(w2cosa).
2.10. Два тела массами m1 и m2 находятся на стержне, по которому они могут свободно двигаться. Тела соединены нитью длиной L. Стержень вращается с угловой скоростью w относительно вертикальной оси вращения. Определить, на каком расстоянии от оси вращения установятся тела.
x1 = m1L/(m1 + m2), x2 = m2L/(m1 + m2).
2.11. Радиус планеты Марс составляет 0,53 радиуса Земли, а плотность - 0,74 плотности Земли. Найти ускорение свободного падения на Марсе.
3,86 м/с2.
2.12. Найти линейную скорость и период обращения искусственного спутника Земли по круговой орбите на расстоянии Н=R от поверхности Земли, где R = 6400 км - радиус Земли. Ускорение свободного падения на поверхности Земли принять равным 9,8м/с2.
v = 5, б км/с; Т = 4 ч.
2.13. Пуля попадает в шар массой М, висящий на нити длиной L, и застревает в нем. С какой максимальной скоростью может лететь пуля, чтобы нить не оборвалась? Максимальная сила натяжения, которую выдерживает нить, равна FMAX, масса пули m0.

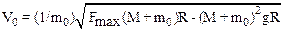
2.14. Определить угловую скорость w вращения двойной звездной системы. Массы звезд М1 и М2, расстояние между их центрами R. Найти также ускорения, с которыми движутся звезды.
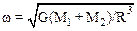 ; a1 = GМ2 / R2; a2 = GМ1 / R2.
; a1 = GМ2 / R2; a2 = GМ1 / R2.
2.15. Найти первую космическую скорость на планете, масса которой в 3 раза, а радиус в 2 раза больше, чем у Земли. Принять первую космическую скорость на Земле равной 8×103 м/с.
9,8×103 м/с.
2.16. Найти момент инерции: а) тонкого однородного стержня относительно оси, перпендикулярной к стержню и проходящей через его конец, если масса стержня m и длина L; б) тонкой однородной прямоугольной пластинки относительно оси, проходящей через одну из вершин пластинки перпендикулярно к ее плоскости, если стороны пластинки раны a и b, а ее масса равна m.
а) I = mL2/3; б) I = m(a2+b2)/3.
2.17. Тонкая однородная пластинка массы m=0,60 кг имеет форму равнобедренного прямоугольного треугольника. Найти ее момент инерции относительно оси, совпадающей с одним из катетов, длина которого а=200 мм.
I=ma2/6=4,0 г·м2.
2.18. Вычислить момент инерции: а) медного однородного диска относительно оси симметрии, перпендикулярной к плоскости диска, если его толщина b=2,0 мм и радиус R=100 мм; б) однородного сплошного конуса относительно его оси симметрии, если масса конуса m и радиус его основания R.
а) I = πρbR4/2=2,8 г·м2; б) I = 0,3mR2.
2.19. Найти момент инерции тонкого проволочного кольца радиусом R и массы m относительно оси, совпадающей с его диаметром.
I=mR2/2.
2.20. Однородный диск радиуса R имеет круглый вырез (рис. 1). Масса оставшейся части диска равна m. Найти момент инерции такого диска относительно оси, перпендикулярной к плоскости диска и проходящей: а) через точку О, б) через его центр масс.
а) IO = (13/24)mR2; б) IC=(37/72)mR2.
2.21. На ступенчатый блок (рис. 2) намотаны в противоположных направлениях две нити. На конец одной нити действуют постоянной силой F, а к концу другой нити прикреплен груз массы m. Известны радиусы R1 и R2 блока и его момент инерции I относительно оси вращения. Трения нет. Найти угловое ускорение блока.
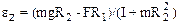
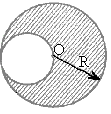 Рис 1.
Рис 1.
| 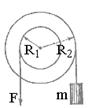 Рис. 2
Рис. 2
|
2.22. Человек массой m1 стоит на краю горизонтального однородного диска массой m2 и радиусом R, который может свободно вращаться вокруг неподвижной вертикальной оси, проходящей через его центр. В некоторый момент человек начал двигаться по краю диска, совершил перемещение на угол 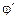 относительно диска и остановился. Пренебрегая размерами человека, найти угол, на который повернулся диск к моменту остановки человека.
относительно диска и остановился. Пренебрегая размерами человека, найти угол, на который повернулся диск к моменту остановки человека.
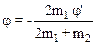
2.23. Два горизонтальных диска свободно вращаются вокруг вертикальной оси, проходящей через их центры. Моменты инерции дисков относительно этой оси равны I1 и I2, а угловые скорости – w1 и w2. После падения верхнего диска на нижний оба диска благодаря трению между ними начали через некоторое время вращаться как единое целое. Найти: а) установившуюся угловую скорость вращения дисков; б) работу, которую совершили при этом силы трения.
а) ω=(I1ω1+I2ω2)/(I1+I2),
б) А = - [I1I2/2(I1+I2)](ω1 -ω2)2.
2.24. На горизонтальную ось насажены маховик и легкий шкив радиусом R=5см. На шкив намотан шнур, к которому привязан груз массой m=0,4кг. Опускаясь равноускоренно, груз прошел путь s=1,8м за время t=3с. Определить момент инерции J маховика. Массу шкива считать пренебрежимо малой.
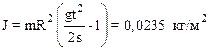
2.25. Вал массой m=100кг и радиусом R=5см вращался с частотой n=8c-1. К цилиндрической поверхности вала прижали тормозную колодку с силой F=40Н, под действием которой вал остановился через t=10с. Определить коэффициент трения f.
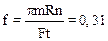
2.26. На цилиндр намотана тонкая гибкая нерастяжимая лента, массой которой по сравнению с массой цилиндра можно пренебречь. Свободный конец ленты прикрепили к кронштейну и предоставили цилиндру опускаться под действием силы тяжести. Определить линейное ускорение а оси цилиндра, если цилиндр: 1) сплошной; 2) полый тонкостенный.
1) a=2g/3; 2) a=g/2.
2.27. Человек стоит на скамье Жуковского и ловит рукой мяч массой m=0.4кг, летящий в горизонтальном направлении со скоростью V=20м/с. Траектория мяча проходит на расстоянии r=0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью w начнет вращаться скамья Жуковского с человеком, поймавшим мяч, если суммарный момент инерции J человека и скамьи равен 6кг·м2.
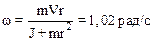
2.29. На краю горизонтальной платформы, имеющий форму диска радиусом R=2м, стоит человек массой m1=80кг. Масса m2 платформы равна 240кг. Платформа может вращаться вокруг вертикальной оси, проходящий через ее центр. Пренебрегая трением, найти, с какой угловой скоростью w будет вращаться платформа, если человек будет идти вдоль ее края со скоростью V=2м/с относительно платформы.
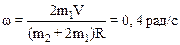
2.29.В центре скамьи Жуковского стоит человек и держит в руках стержень длиной L=2,4 м и массой m=8 кг, расположенный вертикально по оси вращения скамьи. Скамья с человеком вращается с частотой n1=1 с-1. С какой частотой n2 будет вращаться скамья с человеком, если он повернет стержень в горизонтальное положение? Суммарный момент инерции J человека и скамьи равен 6 кг·м2.
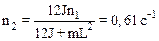
2.30. Чему равен момент инерции тонкого прямого стержня длиной 0,5 м и массой 0,2 кг относительно оси, перпендикулярной к его длине и проходящей через точку стержня, которая удалена на 0,15 м от одного из его концов?
6·10-2 кг·м2.
2.31. На барабан радиусом R=10 см намотана нить, к концу которой привязан груз массой m= 0,50 кг. Найти момент инерции барабана, если груз опускается с ускорением а =1,0 м/с2.
I=mR2(g- a)/ a =4,4·10-2 кг·м2.
2.32. Через блок, масса которого m=100 г, перекинута тонкая гибкая нерастяжимая нить, к концам которой подвешены два груза массами m1 = 200г и m2=300 г. Грузы удерживаются в неподвижном положении. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Чему равно угловое ускорение блока, если его радиус 10 см? Трением пренебречь.
a =(m2-m1)g/(m1+m2+m/2)=1,8 м/с2; ε=(m2-m1)g/(m1+m2+m/2)R=18 с-2.
2.33. Из колодца с помощью ворота поднималось ведро с водой массой m=10 кг. В момент, когда ведро находилось на высоте h=5,0 м от поверхности воды, рукоятка освободилась, и ведро стало двигаться вниз. Определить линейную скорость рукоятки в момент удара ведра о поверхность воды в колодце, если радиус рукоятки R=30 см, радиус вала ворота r =10 см, его масса m1=20 кг. Трением и массой троса, на котором подвешено ведро, пренебречь.
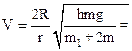 21 м/с.
21 м/с.
2.34. Маховик массой m1=l,0 кг укреплен на шкиве радиусом r=5,0 см и массой m2=200 г, который приводится во вращение с помощью опускающейся гири массой m3=500 г, привязанной к концу намотанной на шкив веревки. Через какое время скорость маховика достигнет n=5,0 об/с? Считать, что вся масса маховика распределена по его ободу радиусом R=40 см.
t=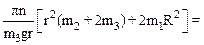 21 с.
21 с.
Пример 3.1.
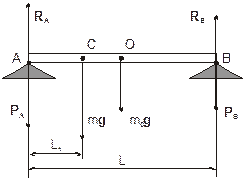
Горизонтальная балка длиной L=4 м и массой m0=200 кг лежит на опорах А и В. к балке в точке С, удаленной на расстояние L1=1,5 м от опоры А, подвешен груз массой m=300 кг. Найти силы давления балки на опоры.
РA=?РB=?
L=4 м, m0=200 кг, L1=1,5 м, m=300 кг
Решение
Воспользуемся вторым условием равновесия, выбрав в качестве полюса точку А:
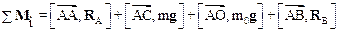 ,
,
где (см. рисунок) АА=0, АС=L1, АО=L/2, AB=L.
|
Переходя к проекции на ось Z, имеем следующее уравнение в скалярной форме:
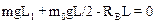 .
.
Решая полученное уравнение относительно реакции RB опоры В, получим:
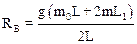 .
.
Искомая сила давления РВ, по третьему закону Ньютона численно равна силе реакции опоры RB. Силу давления на опору А, обозначенную как РА найдем аналогичным способом, приравняв нулю результирующий вращательный момент относительно точки В.
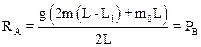 .
.
Задачи к главе 3 для самостоятельного решения
3.1. Однородный стержень длиной 1,0 м и массой 5,0 кг подвешен горизонтально на двух параллельных веревках одинаковой длины. К стержню прикреплен груз массой 10 кг на расстоянии 0,25 м от одного из его концов. Определить натяжения веревок. (49 Н; 98 Н)
3.2. Через блок, прикрепленный к динамометру, переброшен канатик. Один конец канатика закреплен так, что образует угол a=60 градусов с вертикалью (рис. 1). К другому концу подвешен груз массой m=5,0 кг. Определить показания динамометра.
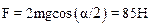
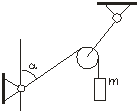 Рис. 1
Рис. 1
| 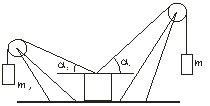 Рис.2
Рис.2
|
3.3. На горизонтальной плоскости лежит груз массой m=10 кг, к которому прикреплены веревки, перекинутые через блоки (рис. 2). К концам веревок подвешены грузы m1 и m2. Определить наибольшее значение массы груза m1, при котором система будет еще находиться в равновесии, если m2=5,0 кг, a1=45 градусов, a2=30 градусов, а коэффициент трения груза о горизонтальную плоскость m=0,50. Массами блоков и веревок и трением в блоках пренебречь.
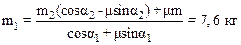
3.4. Однородный стержень массой m=2,0 кг подвешен на двух нитях одинаковой длины, равной a=50 см (рис. 3). Определить длину стержня, если натяжение нитей F=30 H.
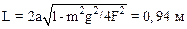
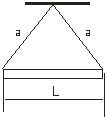 Рис.3 Рис.3
| 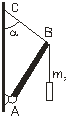 Рис.4 Рис.4
| 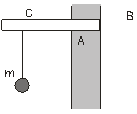 Рис.5 Рис.5
|
3.5. Стержень АВ массой m1=5,0 кг шарнирно прикреплен нижним концом к вертикальной стенке (рис. 4). К верхнему концу стержня, который привязан к стенке веревкой СВ, подвешен груз массой m2=3,0 кг. Определить натяжение веревки СВ, если ее длина в два раза меньше длины стержня АВ.
21 Н
3.6. На наклонной плоскости с углом наклона 35 градусов стоит однородный прямой цилиндр радиусом 10 см. Чему равна наибольшая высота цилиндра, при которой он еще не опрокинется?
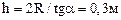
3.7. Однородная горизонтальная балка длиной 1,5 м и массой 50 кг закреплена в стене толщиной 50 см так, что опирается на нее в точках А и В (рис. 5). К свободному концу балки подвешен груз массой 100 кг. Определить силы реакций в опорах А и В.
FA=3,7 кН; FB=2,2 кН
3.8. Однородный шар массой 2 кг прикреплен к вертикальной стене с помощью нити (рис. 6). С какой силой шар давит на стену, если нить образует с ней угол a=30 градусов? Трение не учитывать.
F=FTtga=11 Н
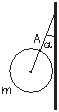 Рис.6
Рис.6
| 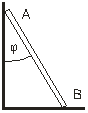 Рис. 7
Рис. 7
| 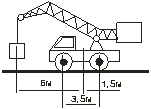 Рис. 8
Рис. 8
|
3.9. При каком наименьшем значении коэффициента трения между стеной и шаром (рис.6) точка А, в которой закреплена нить, и центр шара будут находиться на одной вертикали?
μ=1
3.10. Лестница АВ опирается концом А на вертикальную гладкую стену, а концом В- на пол (рис.7). Коэффициент трения лестницы о пол m=0,3. Чему равно наибольшее значение угла j, образованного лестницей с вертикальной стеной, при котором лестница будет еще находиться в равновесии?
tgφ=2μ; φ=31˚
3.11. На грузовом автомобиле установлен подъемный кран (рис.8). Масса автомобиля вместе с краном 3×103 кг. Расстояние между осями передних и задних колес 3,5 м. Какой максимальный груз может поднять этот кран, если задняя ось и точка, в которой подвешен груз, находятся на расстояниях 1,5 и 6 м от вертикальной плоскости, проходящей через масс автомобиля с краном?
1,5·103 кг
3.12. Найти координаты центра масс системы, состоящей из 4 шариков массами m2=200, m3=300, m4=400 и m1=100 г, которые расположены в вершинах и центре равностороннего треугольника со стороной 20 см. Координатные оси направить так, как указано на рисунке 9.
XC=0,12 м; YC=0,058 м
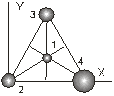 Рис.9 Рис.9
|  Рис.10
Рис.10
| 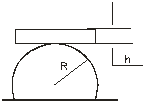 Рис.11 Рис.11
|
3.13. Определить положение центра масс стержня, состоящего из двух частей одинаковой длины и одинакового поперечного сечения, одна из которых свинцовая, а вторая железная, если его общая длина 0,50 м.
Центр масс смещен в сторону свинцовой части на
расстояние 0,25 м от геометрического центра стержня
3.14. В однородном диске диаметром 60 см вырезано круглое отверстие диаметром 20 см, центр которого находится на расстоянии 8,0 см от центра диска (рис.10). Определить положение центра масс диска.
Центр масс смещен на 0,01 м от центра диска
3.15. Брусок толщиной h лежит на неподвижном цилиндре, радиус которого R (рис.11). При каком соотношении между h и R брусок будет находиться в положении устойчивого равновесия? Считать, что трение между бруском и цилиндром достаточно велико.
h<2R
3.16. Масса колеса равна 100 кг, радиус 0,5 м. Какую минимальную силу можно приложить к колесу, чтобы перекатить его через балку высотой 0,10 м? При каком минимальном коэффициенте трения между колесом и выступом это можно сделать?
294 Н, mМИН=0,375.
3.17. Однородный стержень подвешен за концы на двух пружинах, у которых коэффициенты упругости равны k1 и k2. В нерастянутом состоянии длина пружин одинаковая, масса единицы длины стержня q. Под каким углом к горизонту будет висеть стержень при равновесии? Где нужно прикрепить вторую пружину, чтобы стержень висел горизонтально? Длина стержня ℓ.
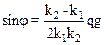 , на расстоянии
, на расстоянии 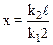 от середины стержня
от середины стержня
3.18. Под каким минимальным углом к горизонту нужно приложить силу к верхнему ребру прямоугольного ящика длиной l и высотой h, чтобы он перемещался, не переворачиваясь? Коэффициент трения равен f. Какова должна быть величина этой силы, если масса ящика равна m?
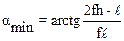 ,
, 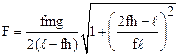
3.19. В открытый с обеих сторон полый цилиндр радиусом R, стоящий торцом на горизонтальной плоскости, положили два одинаковых шара радиусом r > R/2 и массой m. При какой минимальной массе М цилиндра шары его не опрокинут? Поверхности шаров и цилиндра считать гладкими, стенки цилиндра тонкими.
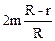
Пример 6.1.
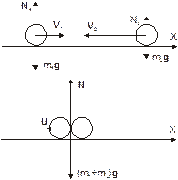
Два шарика массами m1 и m2 движутся навстречу друг другу по идеально гладкой поверхности со скоростями V 1 и V 2. Определите скорость U шариков после абсолютно неупругого удара.
U=?
m1, V1, m2, V2
Решение
На шарики действуют сила тяжести и сила реакции опоры, однако результирующаяих равна 0, т. е. можно применить закон сохранения импульса:
P І = Р ІІ (1)
здесь P І = p 1 + р 2 – импульс системы до взаимодействия (p 1 = m1 V 1, p 2 = m2 V 2), Р ІІ – импульс системы после взаимодействия, Р ІІ = (m1 + m2) U.
|
Выберем ось X вдоль направления движения первого шарика и запишем (1) в проекциях на ось X:
m1V1 - m2V2 = (m1 + m2)U,
откуда следует:
U=(m1V1- m2V2)/(m1+m2).
Пример 6.2.
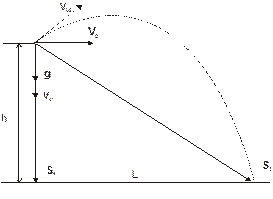
На высоте Н = 80 м снаряд, летящий горизонтально со скоростью V0 = 100м/с, разрывается на два равных осколка. Первый осколок через t1 = 2с падает в эпицентр взрыва. Определить дальность полета второго осколка L.
L=?
H=80 м, V0=100 м/c, t1=2c
Решение
Запишем уравнения кинематики для обоих осколков снаряда, учитывая (см. рис.) равнопеременный характер движения:
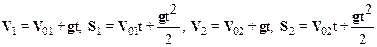 . (1)
. (1)
Эти уравнения в проекциях на оси координат имеют вид: 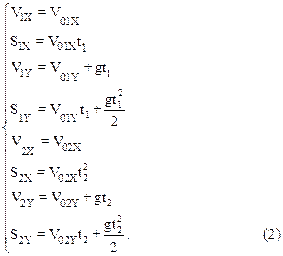
|
Из чертежа видно, что S1Y=S2Y=h, S2X=L. Поскольку первый осколок упал непосредственно под эпицентром взрыва, то S1X=V01Xt1=0. На этом основании можно записать, что V01X=0. С учетом сказанного перепишем систему (2) следующим образом:
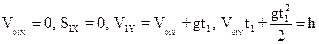
и
|
|
|
|
|
Дата добавления: 2013-12-12; Просмотров: 20262; Нарушение авторских прав?; Мы поможем в написании вашей работы!